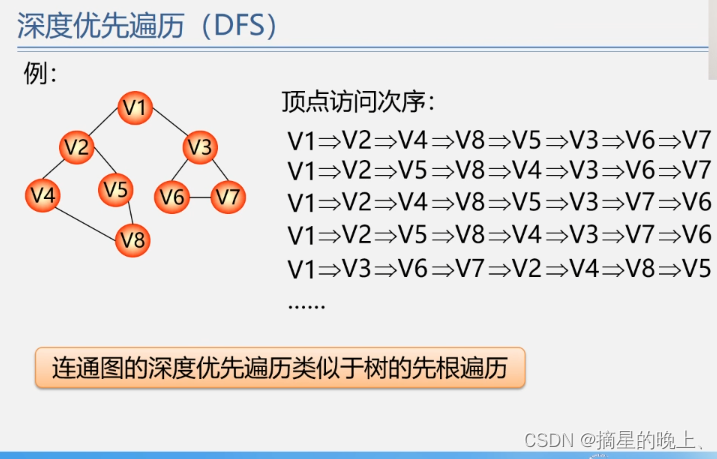
上一讲我们介绍了卷积神经网络和多层感知机，也就是全链接网络。他们在网络架构上是串行的结构，也就是在每一层与每一层之间，前面一层的输出，是后面一层的输入。

在神经网络里面，我们可能会有更加复杂的结构，比如，在每层之间有分支，甚至说要把每一层 的输出再往前作为输入。

我们来介绍两种比较复杂的神经网络结构：

同时我们要思考，当我们遇见一个比较复杂的结构的时候，我们想要实现它，我们要怎么办？

首先回顾一下上节课的知识：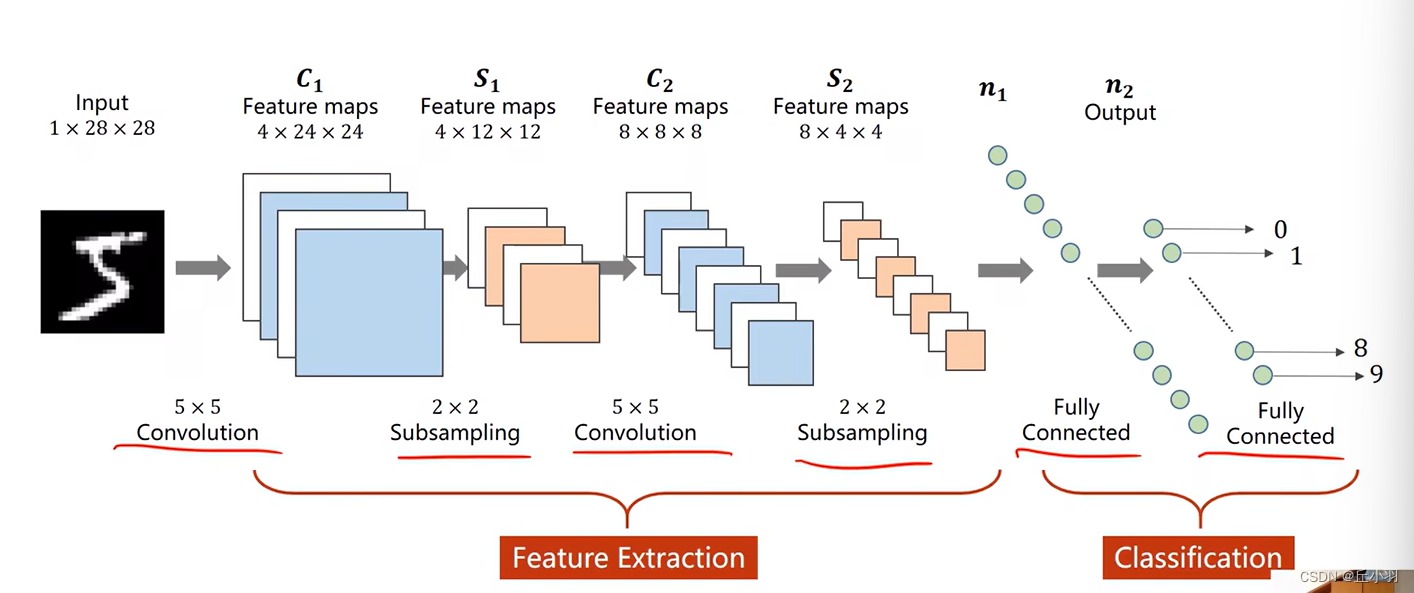

这种网络结构很类似lenet5。接下来我们来看一下不是串行的网络结构。

第一个网络结构是GoogleNet：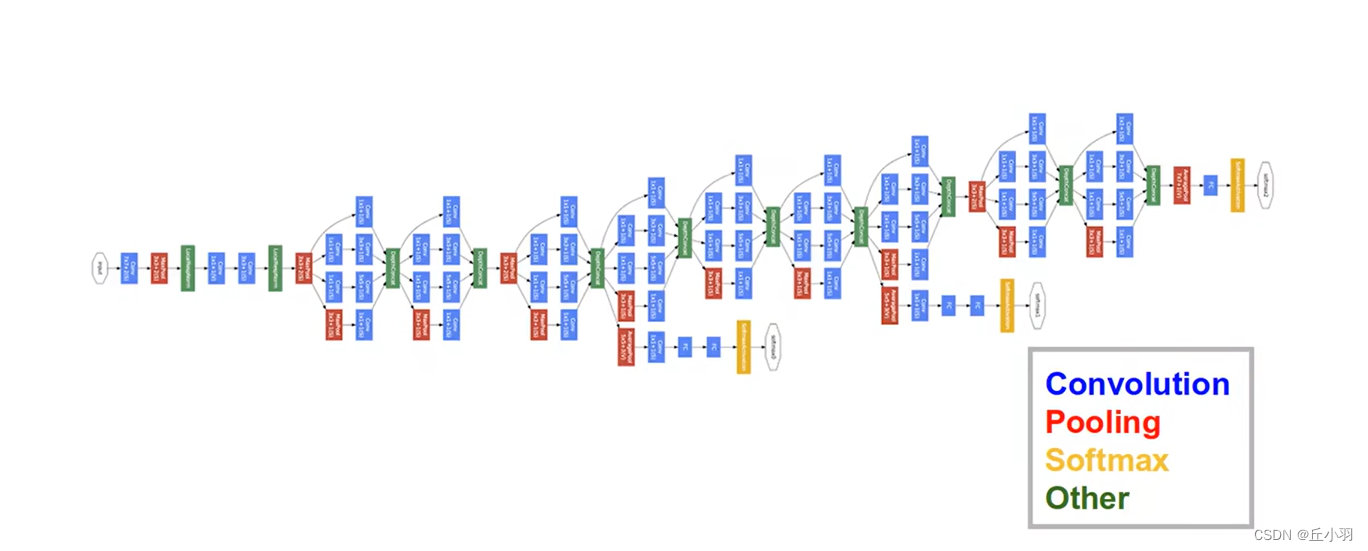

看到这个网络结构，大部分同学就会傻眼，我们要是一个一个对象去定义的话，那我们需要定义好多时间，而且就算写完，代码也会非常的长。

在编程语言里面，我们要尽可能的减少代码的冗余，重复多了容易出错，且不容易维护。
在C语言里面，我们使用函数我们使用函数来减少代码的冗余，在面向对象里面，我们使用类来减少代码的冗余，所以这里面，我们就首先观察有没有相似的结构。

我们注意圈住的部分是一样的。

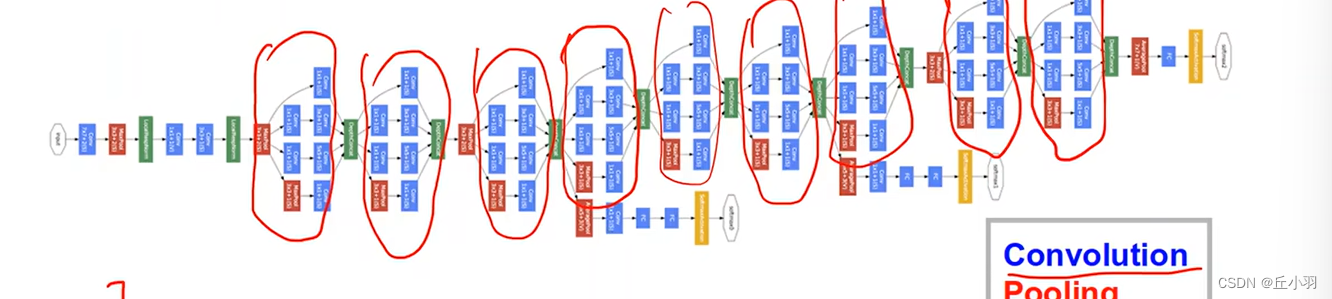
我们可以将这些部分封装成一个类，然后再将他们串起来。

在GoogleNet里面，我们将每一个块儿，就是我们圈出来的部分，称之为Inception。

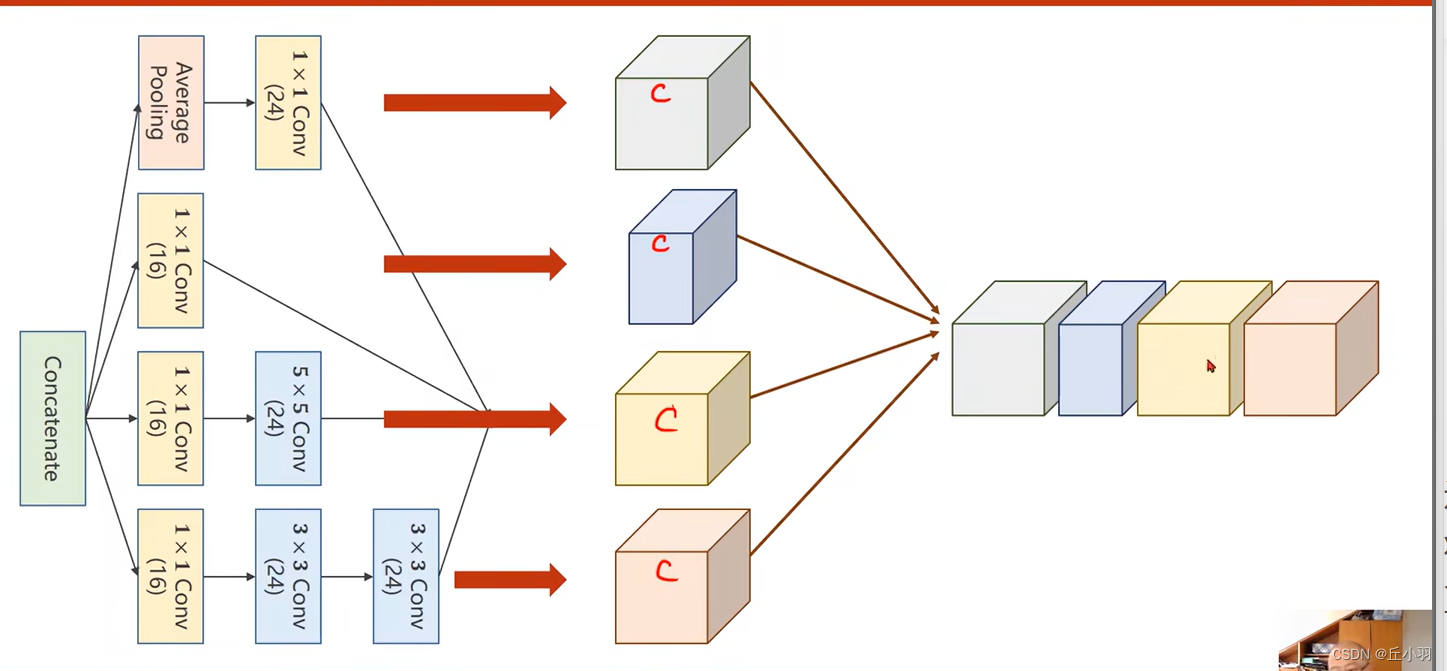
接下来我们来看一下，Inception模块是怎么实现的：

这是一个比较典型的例子，其实Inception模块有好多种构造的方式，上图只是其中一种，首先我们要考虑inception模块为什么要构造成这样。
在构造神经网络的时候，有一些超参数是比较难选的，比如说卷积核的大小（面积，长乘宽），GoogleNet的特点是：我们不确定哪一个卷积核比较好用，所以我们在一块儿里面把所有可能好用的卷积核都放进去，所有卷积都用一下，然后将他们的结果挪到一起，将来，那个好用，其对应的权重就比较大，而其他的就比较小，显然，我们提供了几种候选的卷积核的配置，将来在处理的过程中，自然保留最优的。

Concatenate表示把张量拼接到一起。实现如下图：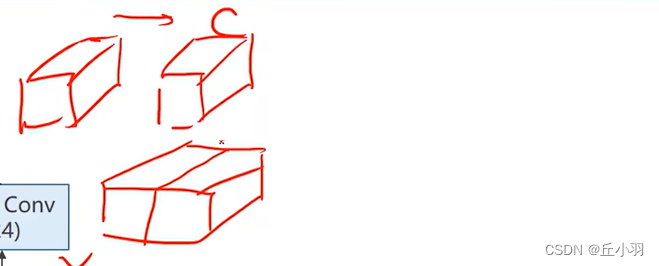

Average Pooling表示均值池化。

显然，我们经过每条路径处理之后，可能不同的只能是Channel，通道数，WH是不会发生变化的。还是原来的宽度和高度（就算计算出来的不是，对计算结果进行广播即可）。在均值池化过程中，我们可以先对得到的结果（进行池化前）进行padding，即广播过程，例如我们需要对得到的张量进行3*3平均池化处理，我们首先要将得到的张量进行扩维度，使之padding=1，然后进行3*3池化，得到的结果与输入的大小是相同的。

我们要考虑比较多的卷积是1*1的卷积，它表示我们的卷积核就是1*1的，它表示拿我们的权重乘我们的每一个像素（遍历）。得到卷积之后的结果。

显然1*1的卷积核的数量等于输入的通道数量。当然，之后我们还要进行求和：

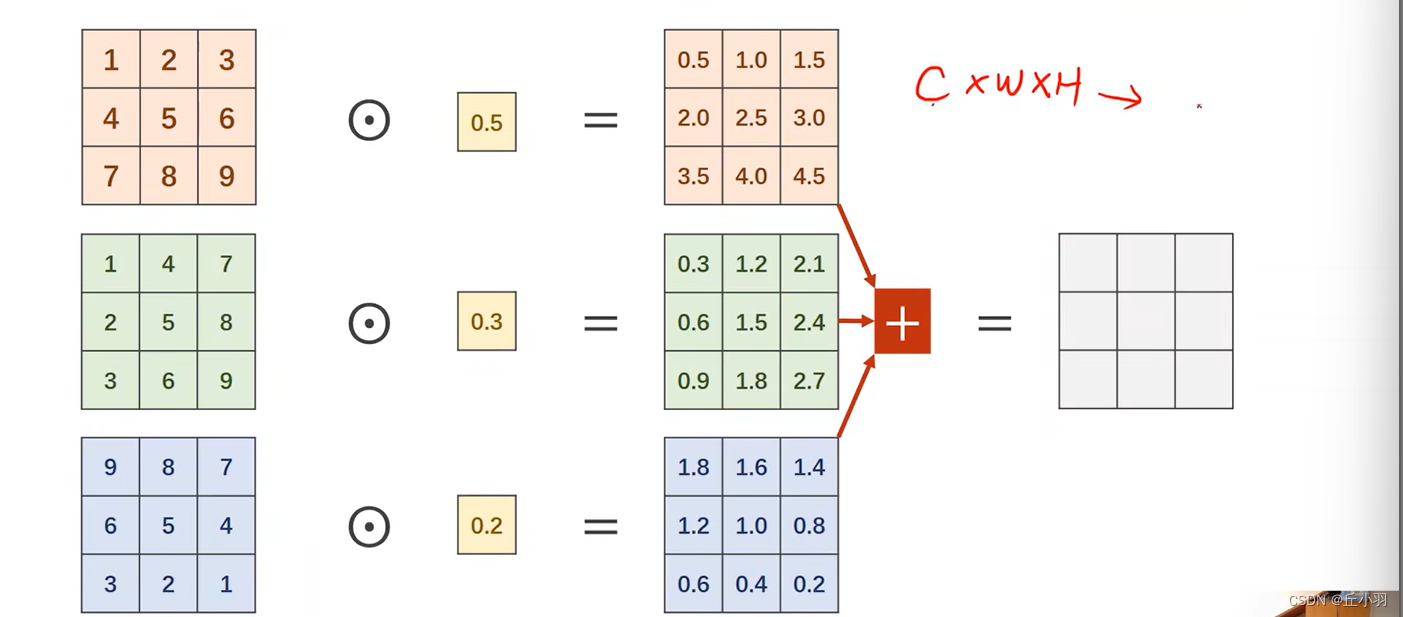
显然，不管我们输入的通道是多少，其输出一定只是一个通道。这个时候我们就能将输入的所有信息融合到一起了。

信息融合并不难理解，我们在中学阶段就学习过信息融合，我们在高中的时候，经常会有模考，模拟考试，考完之后，学校要评价，模拟考试有很多科目组成，例如是五个科目，那我们的成绩就是五维空间的向量，我们对不同的科目取不同的权重，得到一个综合得分，就叫做信息融合。求总分的过程就是信息融合，我们的总分中包含了我们所有科目的信息。

1*1的卷积的作用是改变通道数量。从C1个通道转化为C2个通道。

其他卷积也可以改变通道数量，为什么我们这么钟爱于1*1的卷积？下图会给你答案：

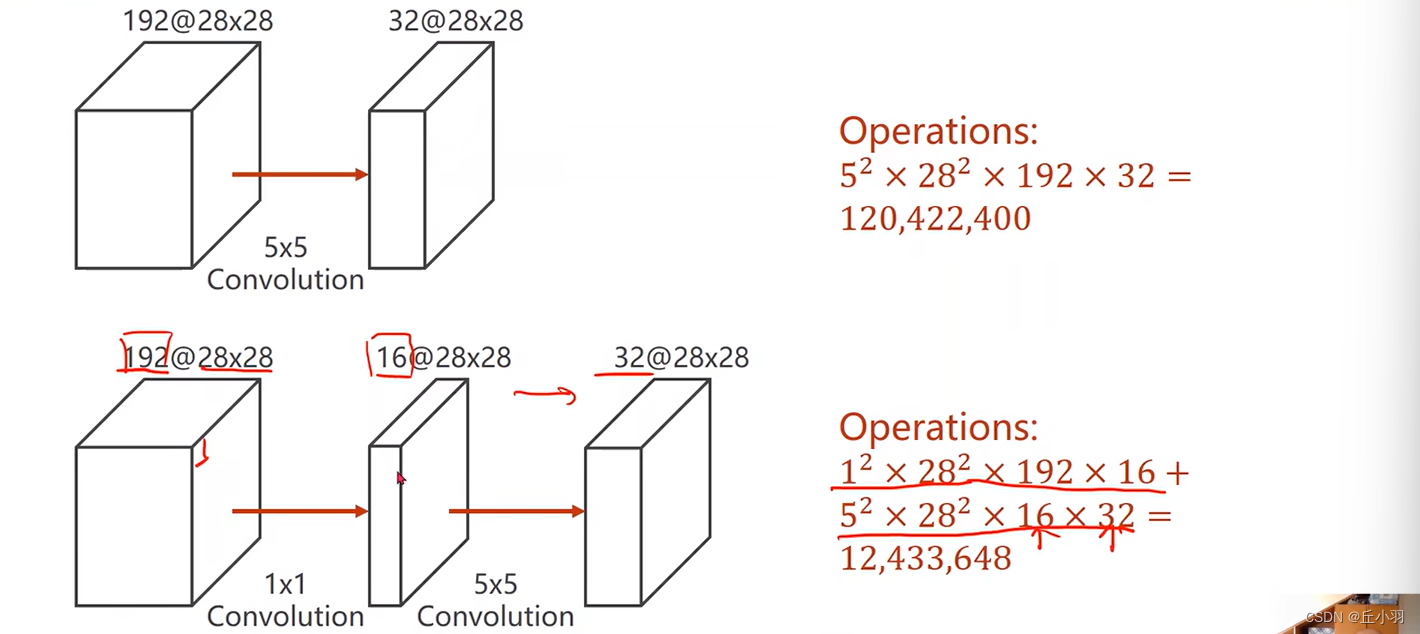
这样来看，我们将数据进行卷积，得到的结果都是32*28*28的张量，但是后者的运算量只有前者的将近10%。跑起来更快。原来需要十个小时，现在只需要一个小时，很节省成本。（为什么我们不直接使用1*1的卷积将其转化为32*28*28呢？我们需要使用更大面积的卷积来综合更多的信息）。

接下来我们进行拼接：

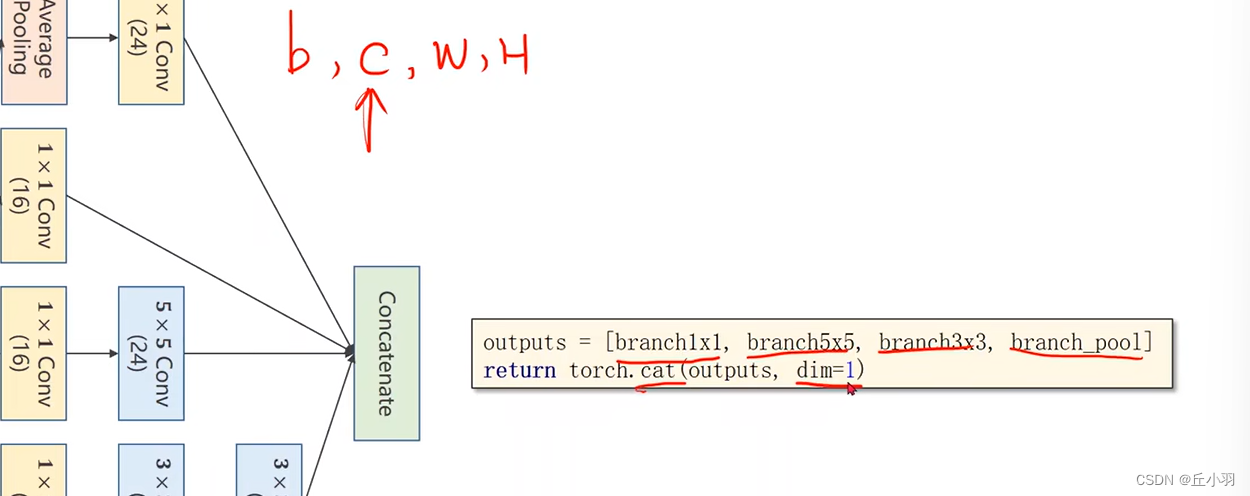
我们沿着第一个维度进行拼接，第一个维度是通道，注意，这里不再是xyz轴。。。

下面我们来介绍另外一种网络：Residual nets

这个神经网络的思考如果我们将3*3的卷积一直不停的堆下去，我们的效果会不会更好。

对于cifar10进行实验发现，20层的卷积相比于56层的卷积效果要好，无论是训练集还是测试集。
说明我们将网络堆的越来越高并不一定结果会更好，当然可能是过拟合或者其他的一些情况，其中有一种可能叫做梯度消失。

所谓的梯度消失：因为我们做的是反向传播，所以我们需要使用链式法则，将一连串的数据进行相乘。假设我们的每一处的梯度都是小于1的，我们在反向传播的过程中如果不断的乘以小于1的值，那么我们的结果就会越来越趋近于0，当无限趋近于0的时候，那么我们的权重就得不到什么更新。离输入比较近的这些块儿，无法得到充分的训练。也有很多方法提出过解决的方法：

我们可以将第一个隐藏层跨过其他的隐藏层，直接接一个转化为需求（输出）维度的层。然后只对这一个从输入到输出的模型（略过其他层）进行训练，训练之后的结果沿着这个比较短的反向传播路径，能够保留更多损失信息，便于对距离输入层比较近的权重进行更新。然后我们将该隐藏层往后移动一格对下一隐藏层执行相同的方法来逐层训练，解决梯度消失的问题。但是在深度学习里面我们这样来的话会是一个很难的事，因为我们的层数太多了。

所以在Residual net里面提供了这样一个块儿：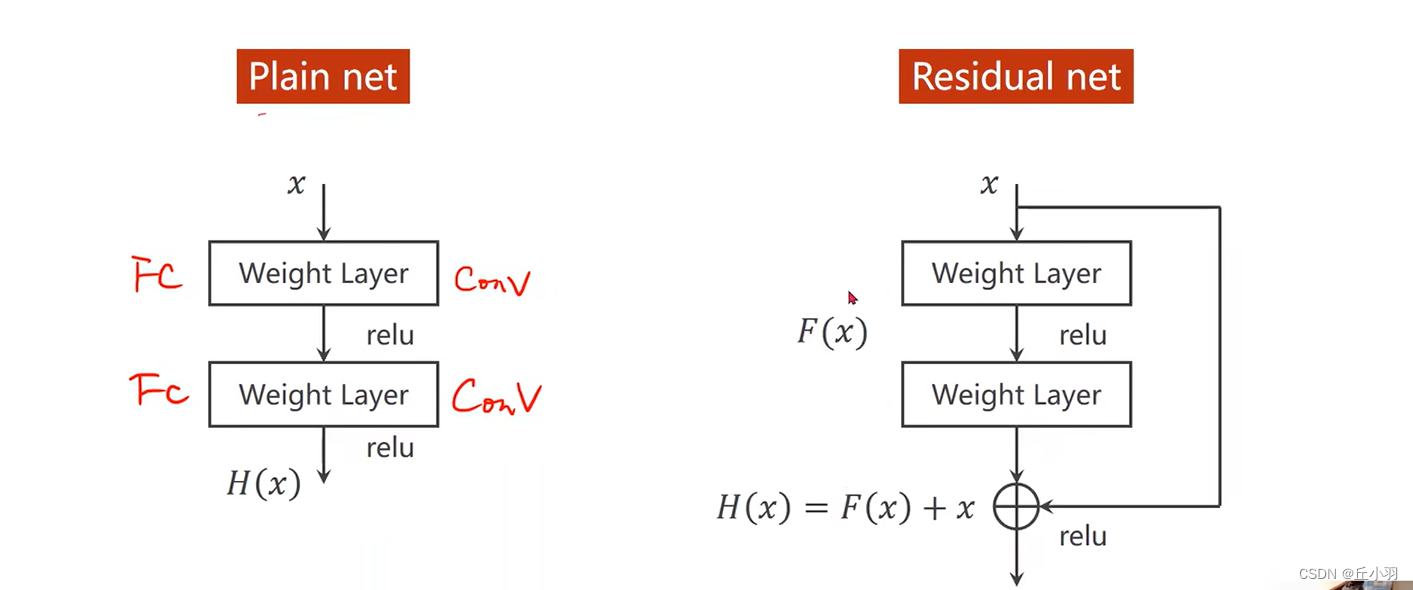

在residual里面加一个链接，在很多工作里面我们也称之为跳链接。

注意，我们的第二个relu先不激活，先将更早的输出x与该层的输出相加后再进行激活。

为什么说它能解决梯度消失问题呢？显然我们在向后传播的过程中，第一层反向传播，会在原有梯度的基础上增加一个1：

当原梯度接近于0的情况下，往回传的梯度能接近于1，若干个这样的数相乘我们就能很好的解决梯度消失问题，能对刚开始的那些层进行很好的训练。需要注意的是，第二个权重层输出的结果和x做加法，要求是输出的结果和x的形状是一样的。

residual net（残差网络）永远滴神！

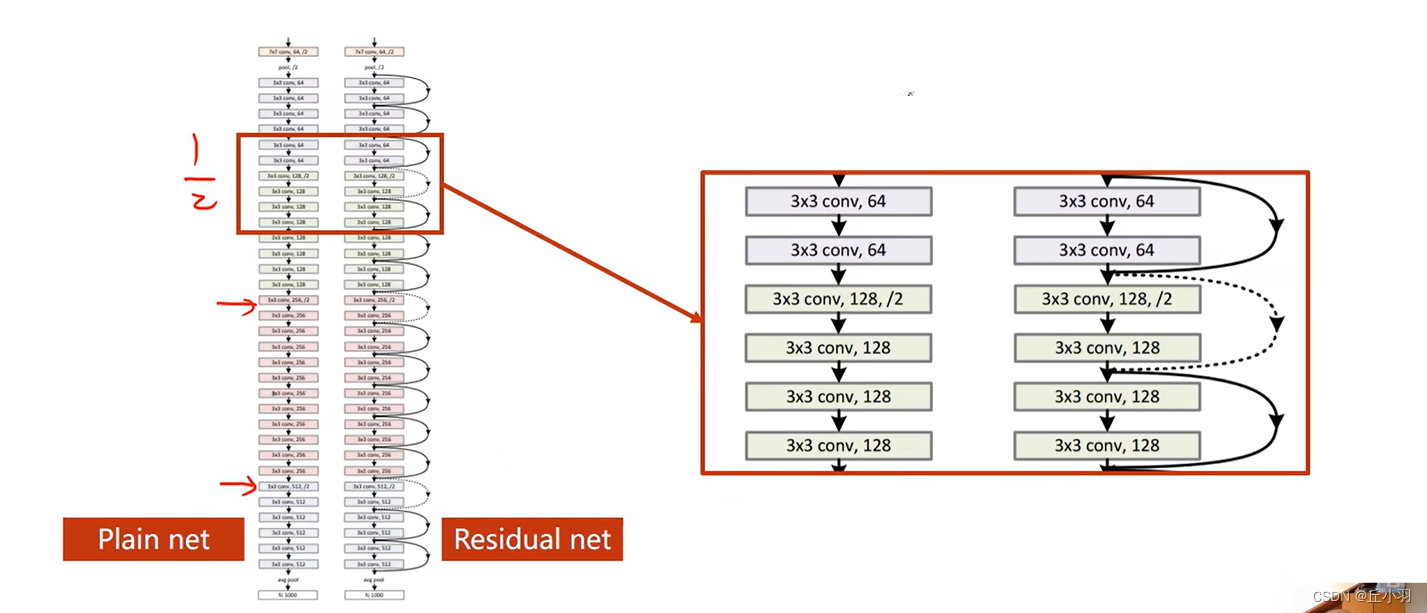
普通神经网络和残差网络的区别。

虚线是指：我们想要输入的x和跳转目的地的形状不一样，我们需要对输入的x进行处理，最简单的处理是我们不做跳链接了，当然我们也可以转化维度之后继续做。（我们可以过一个池化层等）。

总体来看是这样的：

残差块儿我们需要保证输入张量的大小和输出是一样的。

大家看，使用残差网络可以使准确率达到99%：