leetcode 第三弹

链表声明：


 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 *

0206. 反转链表

题目意思：把链表改为逆序

思路：既然改为逆序，那么最简单的想法就是->改为<-，原本指向next的指针指向pre

图片解释：

代码：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head||!head->next) //头结点不存在或者只有一个结点
            return head;
        ListNode *p=head->next;
        ListNode *pre=head;
        while(p){
            ListNode *tmp=p->next;
            p->next=pre;
            pre=p;p=tmp;
        }
            head->next=NULL;
            return pre;
    }
};

改进：

class Solution {//递归思想
public:
    ListNode* reverseList(ListNode* head) {
      if(!head||!head->next){
          return head;
      }  
      ListNode *newHead=reverseList(head->next);//递归反转
      head->next->next=head;
      
      head->next=nullptr;
      //最后一个head的next要设为空；
      //nullptr作为一个字面常量和一个零指针常数，它可以被隐式转换为任何指针类型。
      return newHead;
      }
};

解读：1.主要利用递归思想，大体思路如下：

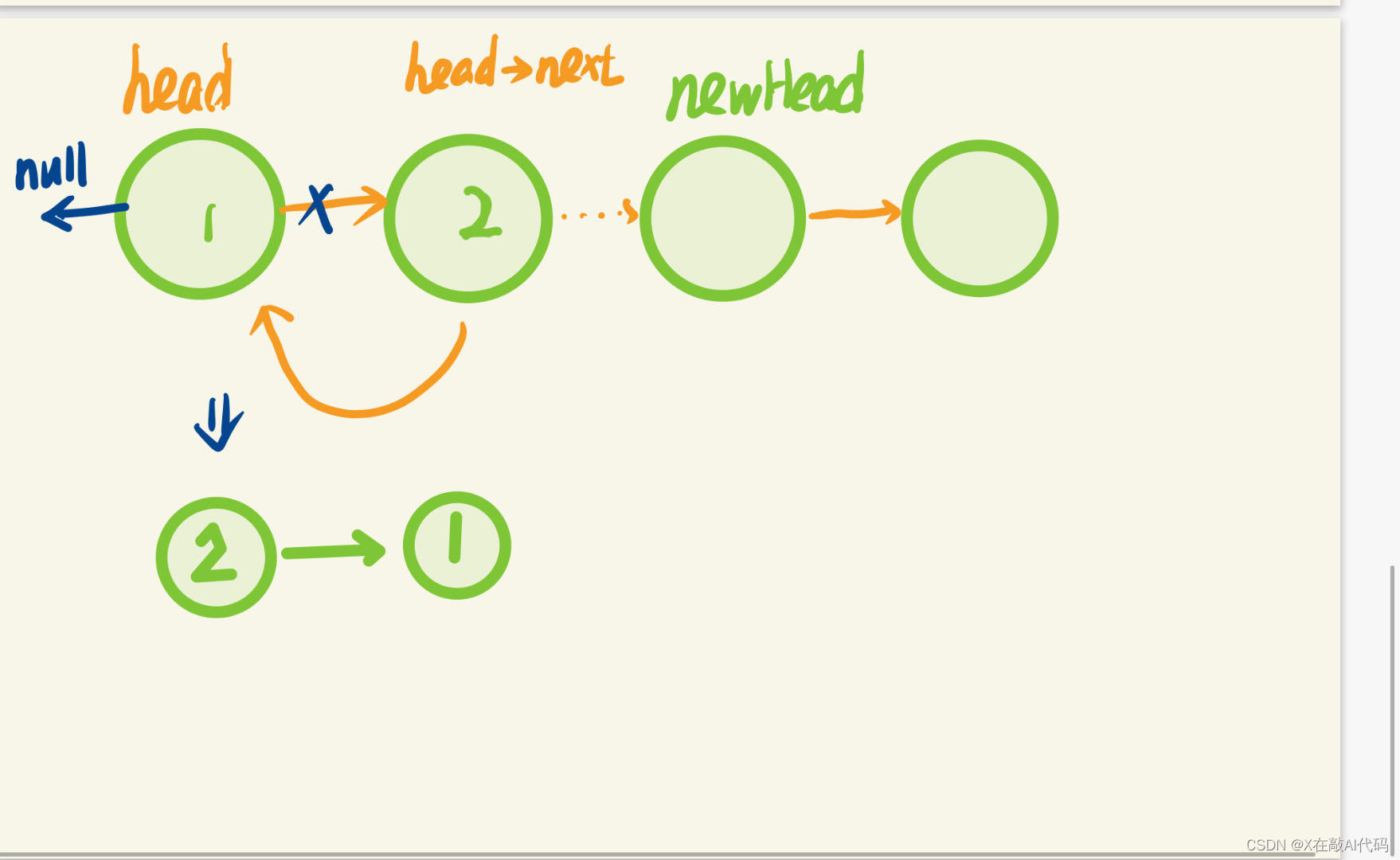
nullptr作为一个字面常量和一个零指针常数，它可以被隐式转换为任何指针类型。
等同于NULL

92.反转链表 II

题目大意：给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

思路： 1.位置 left 到位置 right 的链表节点。遍历找到两个位置。2.将中间部分类似上一题反转（递归解法）3.最后的地方链接一下。

图片解释：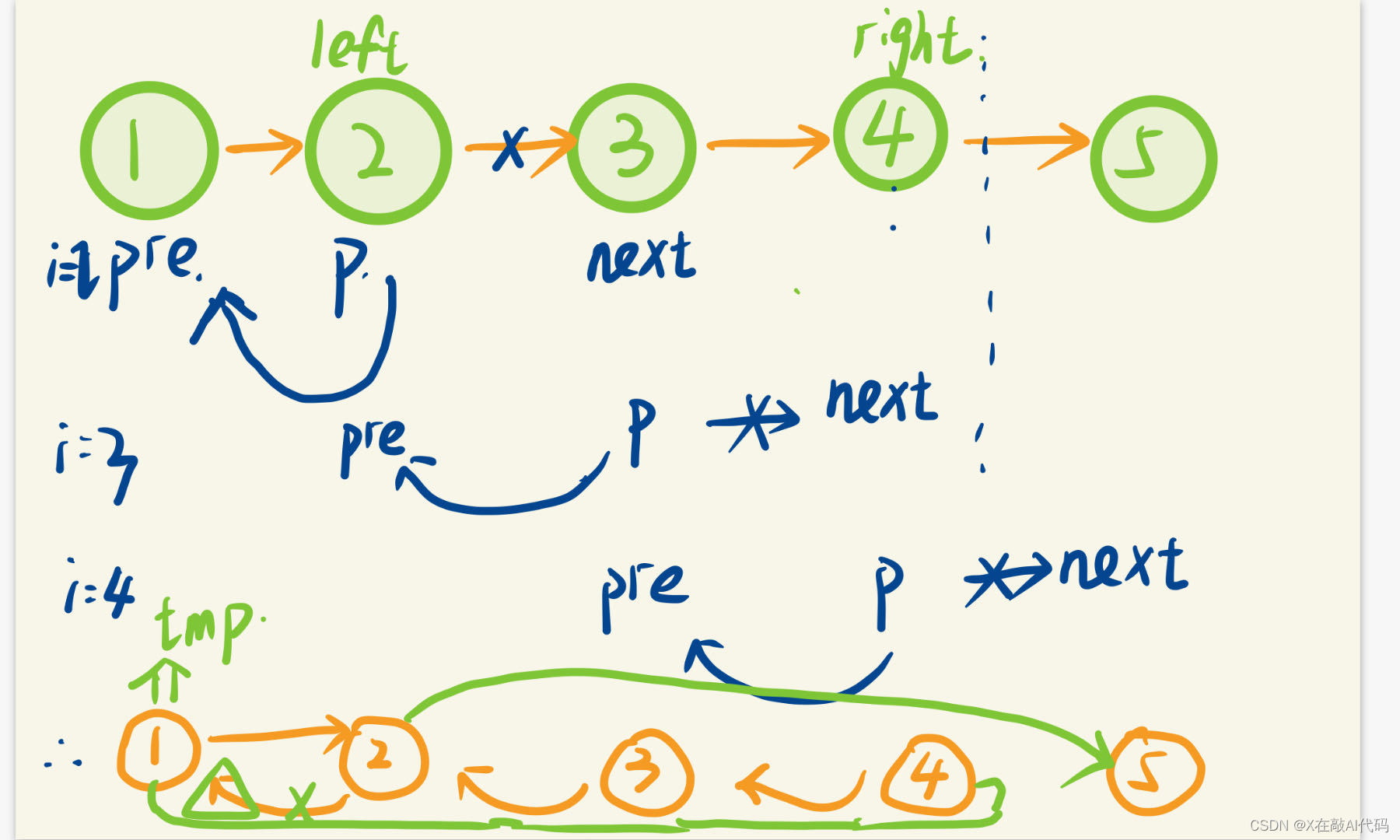

class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        if (right == left)
            return head;
        
        int i = 1; //索引指针，从1开始计数
        ListNode* pre = nullptr;
        ListNode* p = head;
        while (i < left) {
            pre = p;
            p = p->next;
            i++;
        }//找到left对应的节点，将pre指向它的前一个节点，p指向它本身

        ListNode* tmp = pre; // 保存pre的位置，即left的前一个节点
        ListNode* tmp_next = p; // 保存p的位置，即left的节点

        ListNode* next;
        while (i <= right && p != nullptr) {
            next = p->next;
            p->next = pre;
            pre = p;
            p = next;
            i++;
        }//反转从left到right之间的节点
        
        // 将反转后的子链表连接回原链表
        if (tmp != nullptr) {
            tmp->next = pre;
        } else {
            head = pre;
        }
        tmp_next->next = p;
        return head;
    }
};

上面这个代码要注意越界问题，解决这个的话，可以创建头指针，这也是链表中常用的方法。

例如下面的代码：


class Solution {
public:
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        if (left == right) {
            return head;
        }
        
        int i = 1; // 索引指针
        ListNode* dummy = new ListNode(0); // 创建虚拟头节点
        dummy->next = head;
        ListNode* pre = dummy;
        while (i < left) {
            pre = pre->next;
            i++;
        }// 找到左边界的前一个节点
        
        ListNode* p = pre->next; // 当前节点为左边界节点
        ListNode* prev = nullptr;
        ListNode* next = nullptr;
        ListNode* leftNode = p; // 保存左边界节点，反转后将成为尾节点
        
        while (i <= right) {
            next = p->next;
            p->next = prev;
            prev = p;
            p = next;
            i++;
        } // 反转链表
        
        // 连接反转后的链表部分
        pre->next = prev;
        leftNode->next = p;
        
       // ListNode* newHead = dummy->next;
        //delete dummy;
        
        return dummy->next;
    }
};

学习地方：1.令prev==null；使得后续链接更加简化。

ListNode* prev = nullptr;

设置头结点，避免越界问题。（上面代码中没有删除头结点，直接返回头结点的下一个）

ListNode* dummy = new ListNode(0); // 创建虚拟头节点
        dummy->next = head;

ListNode* newHead = dummy->next;//头节点的删除
        delete dummy;
        return newHead

25. K 个一组翻转链表

方法一：栈(这个方法牛逼)//用栈，我们把 k 个数压入栈中，然后弹出来的顺序就是翻转的;用这个可以尝试把前面逆序的给秒掉。

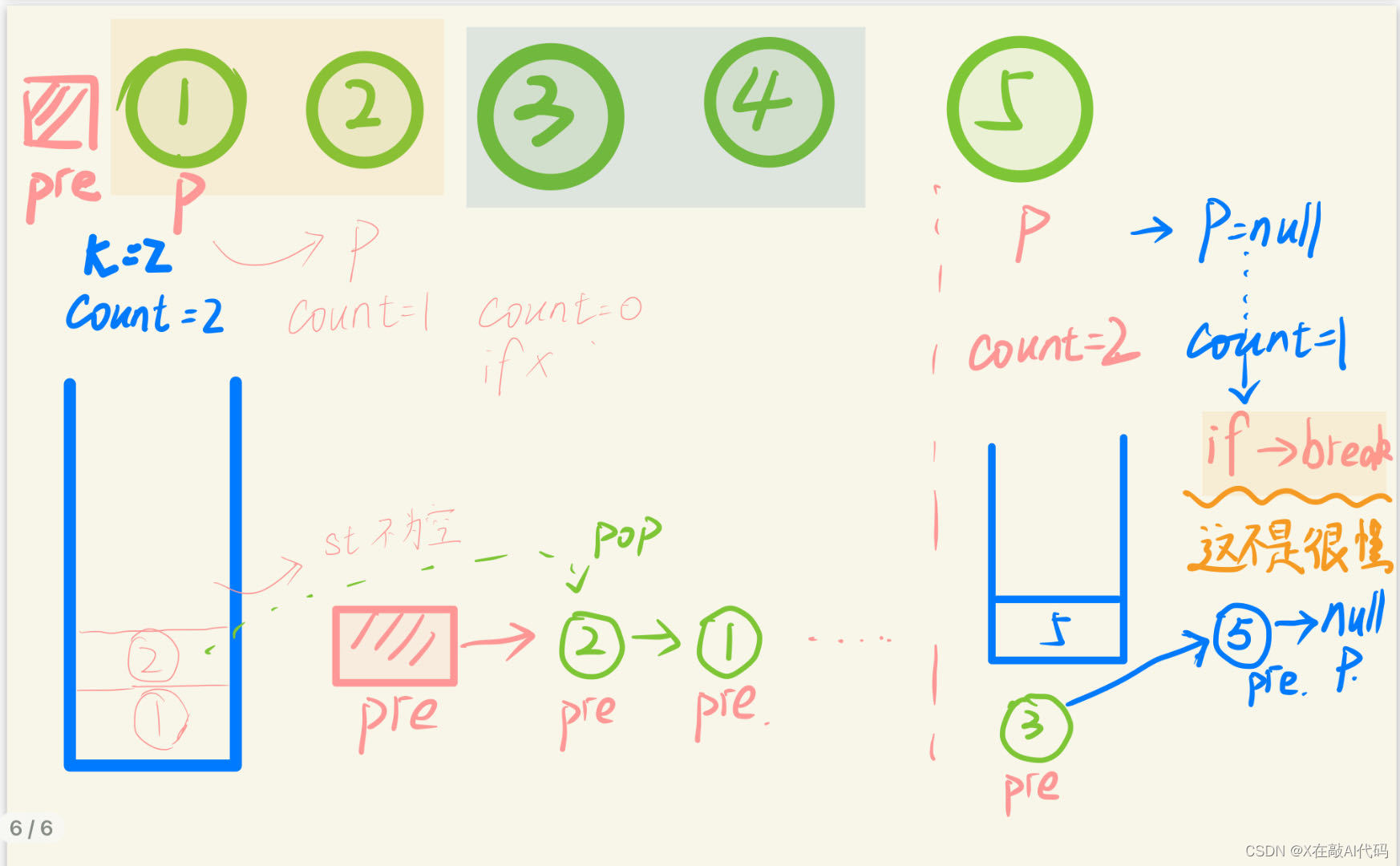
class Solution { //用栈，我们把 k 个数压入栈中，然后弹出来的顺序就是翻转的;
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* dummy = new ListNode(0); // 创建虚拟头节点
        dummy->next = head;
        ListNode* pre = dummy;
        ListNode* p = head;

        while (true) {
            int count = k;       //计数器
            stack<ListNode*> st; //声明栈

            while (count > 0 && p != nullptr) { //越界条件判断
                st.push(p);                     // p进栈
                p = p->next;
                count--;
            }
             if (count > 0) break;//元素不足k个

            while (!st.empty()) {
                pre->next = st.top();
                pre = pre->next;
                st.pop();
            }
            pre->next = p;
            head = p;
        }
        ListNode* newHead = dummy->next; //头节点的删除
        delete dummy;
        return newHead;
    }
};

0206. 反转链表

方法一思路：根据上面做的题，想到的利用栈来解决。

要利用栈判断链表是否为回文链表，可以按照以下步骤进行操作：

1. 创建一个空栈。
2. 遍历链表，将链表节点的值依次入栈。
3. 再次遍历链表，同时将栈顶元素与当前链表节点的值进行比较。
   - 如果相等，则链表继续向后移动，并将栈顶元素出栈。
   - 如果不相等，则链表不是回文链表。
4. 如果链表遍历结束，且栈也为空，则链表是回文链表；否则，链表不是回文链表。

需要注意的是，这种方法会改变原始链表的结构。如果你不希望改变链表结构，你可以使用递归来判断链表是否为回文链表。

这里方便改正代码，我将栈设置为了int类型，也可以向上一题一样设置为

stack<ListNode*> st; //声明栈……

class Solution {//自己思考:利用栈
public:
    bool isPalindrome(ListNode* head) {//
    if(!head||!head->next) return true;
        ListNode* p=head;
        stack<int> st; //声明栈

        while(p){
            st.push(p->val);
           cout<<"st.top()"<<st.top();
            p=p->next;
        }
        ListNode* pp=head;
       
        while(pp!=nullptr){
            if(pp->val==st.top()){
                pp=pp->next;
                st.pop();
               
            }
            else break;
        }
        if(st.empty()) return true;
        return false;
    }
};

方法二：将值复制到数组中后采用双指针。

解释：

确定数组列表是否回文很简单，我们可以使用双指针法来比较两端的元素，并向中间移动。一个指针从起点向中间移动，另一个指针从终点向中间移动。这需要 O(n)O(n)O(n) 的时间，因为访问每个元素的时间是 O(1)，而有 n 个元素要访问。

然而同样的方法在链表上操作并不简单，因为不论是正向访问还是反向访问都不是 O(1)。而将链表的值复制到数组列表中是 O(n)，因此最简单的方法就是将链表的值复制到数组列表中，再使用双指针法判断。

一共为两个步骤：
1.复制链表值到数组列表中。
2.使用双指针法判断是否为回文。

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        vector <int> ans;
        ListNode* p=head;
        while(p){
            ans.push_back(p->val);
            p=p->next;
        }
        int len=ans.size();
        int i=0;int j=len-1;
        while(i<j){
            if(ans[i]==ans[j]){
                i++;j--;
            }
            else break;
        }
        if(i==len/2)return true;
        return false;
    }
};

方法三：方法二的改进版，这个方法将上面建立数组所消耗的0(n)复杂度降为0(1)。

掌握思想即可。代码看看就行。

思路

避免使用 O(n) 额外空间的方法就是改变输入。

我们可以将链表的后半部分反转（修改链表结构），然后将前半部分和后半部分进行比较。
比较完成后我们应该将链表恢复原样。
虽然不需要恢复也能通过测试用例，但是使用该函数的人通常不希望链表结构被更改。

该方法虽然可以将空间复杂度降到 O(1)，但是在并发环境下，该方法也有缺点。
在并发环境下，函数运行时需要锁定其他线程或进程对链表的访问，
因为在函数执行过程中链表会被修改。

算法

整个流程可以分为以下五个步骤：

1.找到前半部分链表的尾节点。
2.反转后半部分链表。
3.判断是否回文。
4.恢复链表。
5.返回结果。

执行步骤一，我们可以计算链表节点的数量，然后遍历链表找到前半部分的尾节点。

我们也可以使用快慢指针在一次遍历中找到：慢指针一次走一步，快指针一次走两步，快慢指针同时出发。当快指针移动到链表的末尾时，慢指针恰好到链表的中间。通过慢指针将链表分为两部分。

若链表有奇数个节点，则中间的节点应该看作是前半部分。

步骤二可以使用「206. 反转链表」问题中的解决方法来反转链表的后半部分。

步骤三比较两个部分的值，当后半部分到达末尾则比较完成，可以忽略计数情况中的中间节点。

class Solution {
public:
    bool isPalindrome(ListNode* head) {
        if (head == nullptr) {
            return true;
        }

        // 找到前半部分链表的尾节点并反转后半部分链表
        ListNode* firstHalfEnd = endOfFirstHalf(head);
        ListNode* secondHalfStart = reverseList(firstHalfEnd->next);

        // 判断是否回文
        ListNode* p1 = head;
        ListNode* p2 = secondHalfStart;
        bool result = true;
        while (result && p2 != nullptr) {
            if (p1->val != p2->val) {
                result = false;
            }
            p1 = p1->next;
            p2 = p2->next;
        }        

        // 还原链表并返回结果
        firstHalfEnd->next = reverseList(secondHalfStart);
        return result;
    }

    ListNode* reverseList(ListNode* head) {
        ListNode* prev = nullptr;
        ListNode* curr = head;
        while (curr != nullptr) {
            ListNode* nextTemp = curr->next;
            curr->next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }

    ListNode* endOfFirstHalf(ListNode* head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast->next != nullptr && fast->next->next != nullptr) {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
};

0021. 合并两个有序链表

方法一：思路：新建一个头结点，直接将小的结点，连接在头结点的后面

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode* dum = new ListNode(0);
        ListNode* cur = dum;
        while (list1 != nullptr && list2 != nullptr) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next;
            }
            else {
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        cur->next = list1 != nullptr ? list1 : list2;
        return dum->next;
    }
};

方法二：直接在原链表上增加。但疯狂越界！！！！

求指正。


class Solution {//直接无脑合并
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(!list1) return list2;
        if(!list2) return list1;
        ListNode* p1=list1;ListNode* p2=list2;
        ListNode* pre;
        while(p2!=nullptr){
            if(p1==nullptr) break;
            if(p1->val < p2->val){
                pre=p1;
                p1=p1->next;
            }
            else{
                pre->next=p2;
                p2->next=p1;
                p2=p2->next;
            }
        }
        if(p1==nullptr) p1->next=p2;
        return list1;
    }
};

思路：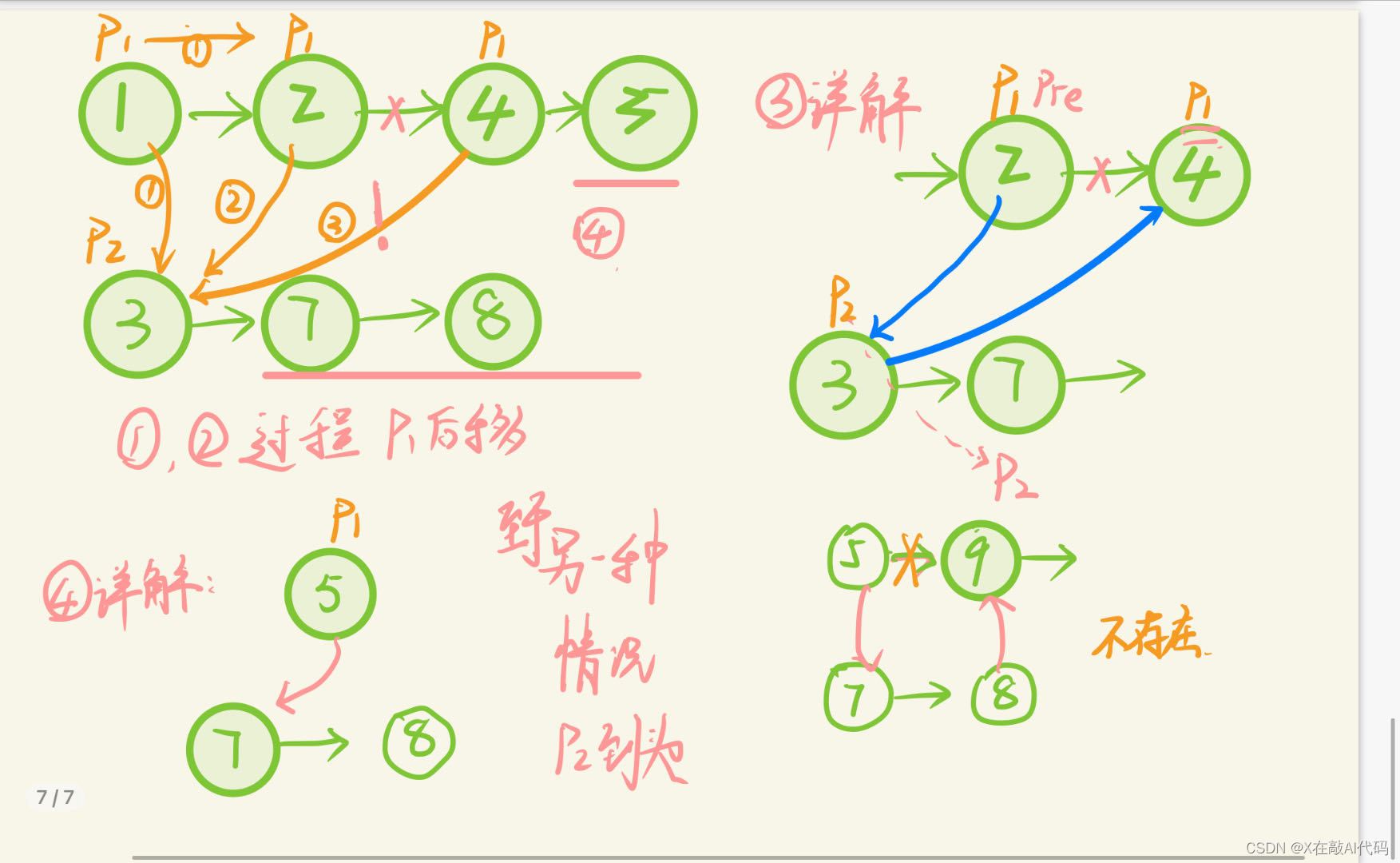

148. 排序链表

以在 O(nlogn) 时间复杂度和常数级空间复杂度下，对链表进行排序。

在做这道题之前不放先看一下147. 对链表进行插入排序

下面是147. 对链表进行插入排序的解析

这道题明确指出使用插入排序，那么插入排序是什么？

插入排序 算法的步骤:

插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
重复直到所有输入数据插入完为止。

下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时，从输入数据中删除一个元素(红色)，并就地插入已排序的列表中。对链表进行插入排序。插入排序的时间复杂度是 O(n^2)，其中 n 是链表的长度。

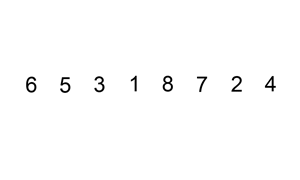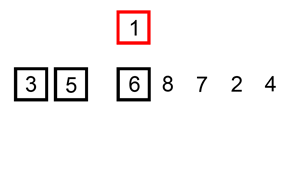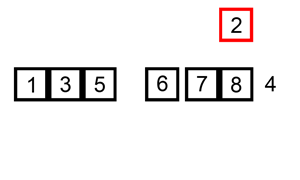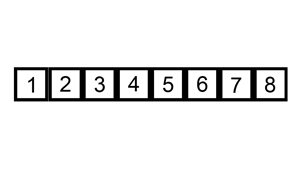
本题思路：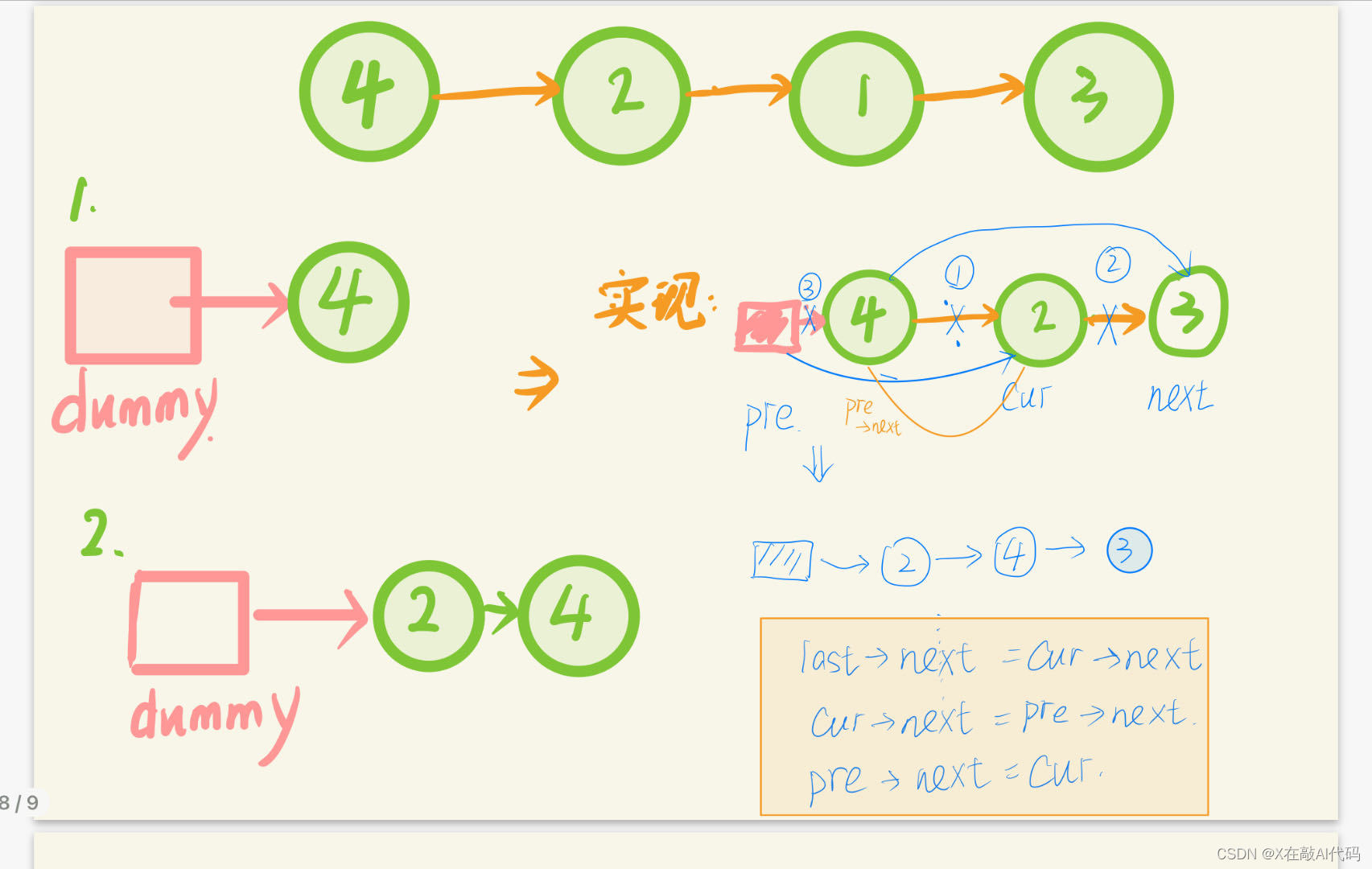

本题代码：last是排好序的链表的最后一个。cur是当前节点。prev是插入位置的前一个。

class Solution {
public:
    ListNode* insertionSortList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        
        // 创建一个哑节点(dummy)，用于处理头节点的特殊情况
        ListNode* dummy = new ListNode(-555);
        dummy->next = head;

        ListNode* last = head;
        ListNode* cur = head->next;
        while (cur) {
            // 如果当前节点的值小于上一个节点的值，需要进行插入排序操作
            if (cur->val < last->val) {
                ListNode* prev = dummy;
                
                // 寻找插入位置的前一个节点
                while (prev->next->val <= cur->val && prev != last) {
                    prev = prev->next;
                }
                
                // 将当前节点从链表中移除
                last->next = cur->next;
                  
                // 将当前节点插入到正确的位置
                cur->next = prev->next;
                prev->next = cur;
            } else {
                last = last->next;
            }
            
            // 移动到下一个节点
            cur = last->next;
        }
        
        return dummy->next;
    }
};

148. 排序链表

跟上道题相比，这道题考虑时间复杂度更低的排序算法。题目的进阶问题要求达到 $O(n \log n)$ 的时间复杂度和 $O(1)$ 的空间复杂度，时间复杂度是的排序算法包括归并排序、堆排序和快速排序（快速排序的最差时间复杂度是 $O(n^2)$ ，其中最适合链表的排序算法是归并排序。

归并排序基于分治算法。最容易想到的实现方式是自顶向下的递归实现，考虑到递归调用的栈空间，自顶向下归并排序的空间复杂度是 $O(logn)$ 。如果要达到 O(1) 的空间复杂度，则需要使用自底向上的实现方式。

方法一：自顶向下归并排序
对链表自顶向下归并排序的过程如下。

图解：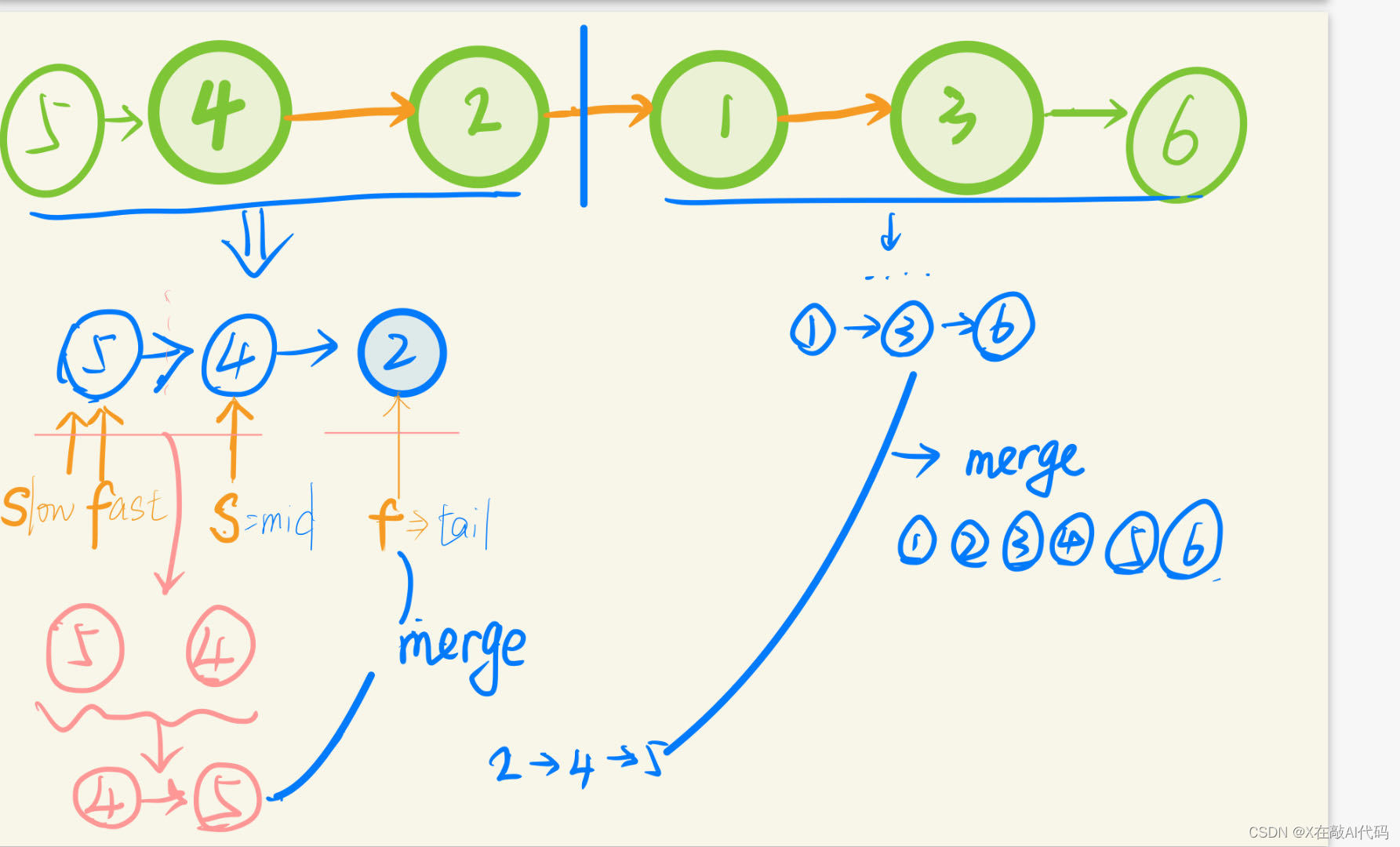

1.找到链表的中点，以中点为分界，将链表拆分成两个子链表。寻找链表的中点可以使用快慢指针的做法，快指针每次移动 2 步，慢指针每次移动 1 步，当快指针到达链表末尾时，慢指针指向的链表节点即为链表的中点。

ListNode* slow = head, *fast = head;
        while (fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next;
            }
        }
        ListNode* mid = slow;

2.对两个子链表分别排序。

3.将两个排序后的子链表合并，得到完整的排序后的链表。可以使用「21. 合并两个有序链表」的做法，将两个有序的子链表进行合并。

 ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }

上述过程可以通过递归实现。递归的终止条件是链表的节点个数小于或等于 1，即当链表为空或者链表只包含 1 个节点时，不需要对链表进行拆分和排序。

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        return sortList(head, nullptr);
    }

    ListNode* sortList(ListNode* head, ListNode* tail) {
        if (head == nullptr) {
            return head;
        }
        if (head->next == tail) {
            head->next = nullptr;
            return head;
        }
        ListNode* slow = head, *fast = head;
        while (fast != tail) {
            slow = slow->next;
            fast = fast->next;
            if (fast != tail) {
                fast = fast->next;
            }
        }
        ListNode* mid = slow;
        return merge(sortList(head, mid), sortList(mid, tail));
    }

    ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }
};

时间复杂度： $O(\log n)$ ，其中 n 是链表的长度。

空间复杂度 $O(\log n)$ ，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。

方法二：自底向上归并排序（这个写起来比较难，注意看代码的注解，很详细）
使用自底向上的方法实现归并排序，则可以达到 $O(1)$ 的空间复杂度。

首先求得链表的长度 $\textit{subLength}$ ，然后将链表拆分成子链表进行合并。

具体做法如下。

用 $\textit{subLength}$ 表示每次需要排序的子链表的长度，初始时 $\textit{subLength}=1$

每次将链表拆分成若干个长度为 $\textit{subLength}$ 的子链表（最后一个子链表的长度可以小于 $\textit{subLength}$ ，按照每两个子链表一组进行合并，合并后即可得到若干个长度为 $\textit{subLength}$ ×2 的有序子链表（最后一个子链表的长度可以小于 $\textit{subLength}$ ×2）。合并两个子链表仍然使用「21. 合并两个有序链表」的做法。

将 $\textit{subLength}$ 的值加倍，重复第 2 步，对更长的有序子链表进行合并操作，直到有序子链表的长度大于或等于 $\textit{subLength}$ ，整个链表排序完毕。

图解：一开始先一个一个排，再两个两个排，再四个……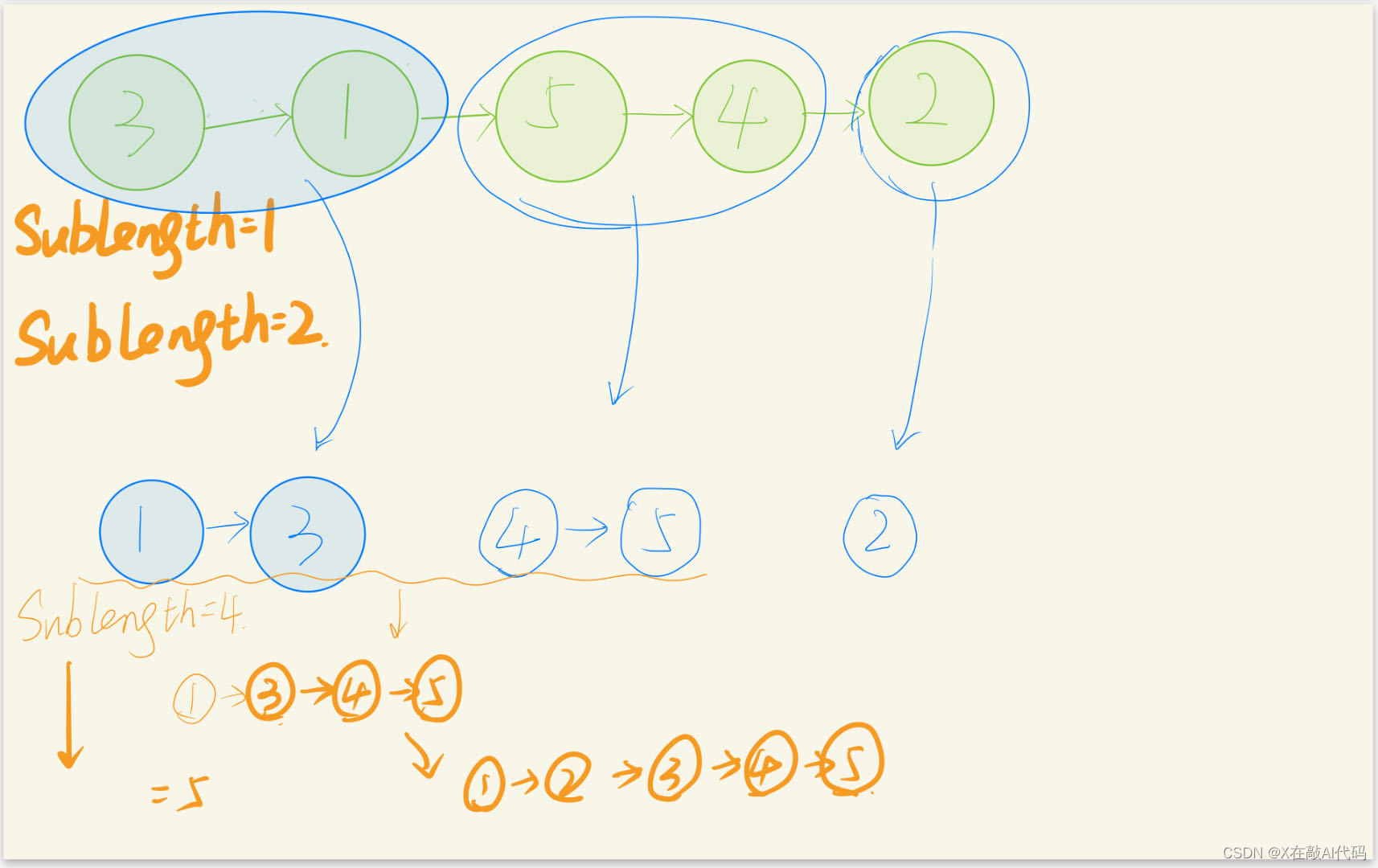

ListNode* sortList(ListNode* head) {
    // 判断链表是否为空
    if (head == nullptr) {
        return head;
    }

    int length = 0;
    ListNode* node = head;

    // 计算链表的长度
    while (node != nullptr) {
        length++;
        node = node->next;
    }

    // 创建一个虚拟头节点，指向原链表的头节点
    ListNode* dummyHead = new ListNode(0, head);

    // 通过子链表的长度进行归并排序
    for (int subLength = 1; subLength < length; subLength <<= 1) {
        ListNode* prev = dummyHead;  // 当前子链表的前一个节点
        ListNode* curr = dummyHead->next;  // 当前子链表的头节点

        // 对当前子链表进行归并排序
        while (curr != nullptr) {
            // 获取第一个子链表的头节点
            ListNode* head1 = curr;

            // 定位到第一个子链表的尾节点
            for (int i = 1; i < subLength && curr->next != nullptr; i++) {
                curr = curr->next;
            }

            // 获取第二个子链表的头节点
            ListNode* head2 = curr->next;

            // 将第一个子链表与第二个子链表断开连接
            curr->next = nullptr;

            // 更新当前指针的位置为第二个子链表的头节点
            curr = head2;

            // 定位到第二个子链表的尾节点
            for (int i = 1; i < subLength && curr != nullptr && curr->next != nullptr; i++) {
                curr = curr->next;
            }

            ListNode* next = nullptr;
            
            // 断开第二个子链表的尾节点与后面的节点的连接
            if (curr != nullptr) {
                next = curr->next;
                curr->next = nullptr;
            }

            // 合并两个子链表
            ListNode* merged = merge(head1, head2);

            // 将合并后的子链表链接到当前子链表的位置
            prev->next = merged;

            // 定位到合并后子链表的尾节点
            while (prev->next != nullptr) {
                prev = prev->next;
            }

            // 更新当前指针的位置为断开连接后的下一个节点
            curr = next;
        }
    }

    // 返回排序后的链表头节点
    return dummyHead->next;
}

merge()函数同0021题，同上一个方法。

ListNode* merge(ListNode* head1, ListNode* head2) {
        ListNode* dummyHead = new ListNode(0);
        ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
        while (temp1 != nullptr && temp2 != nullptr) {
            if (temp1->val <= temp2->val) {
                temp->next = temp1;
                temp1 = temp1->next;
            } else {
                temp->next = temp2;
                temp2 = temp2->next;
            }
            temp = temp->next;
        }
        if (temp1 != nullptr) {
            temp->next = temp1;
        } else if (temp2 != nullptr) {
            temp->next = temp2;
        }
        return dummyHead->next;
    }