框架
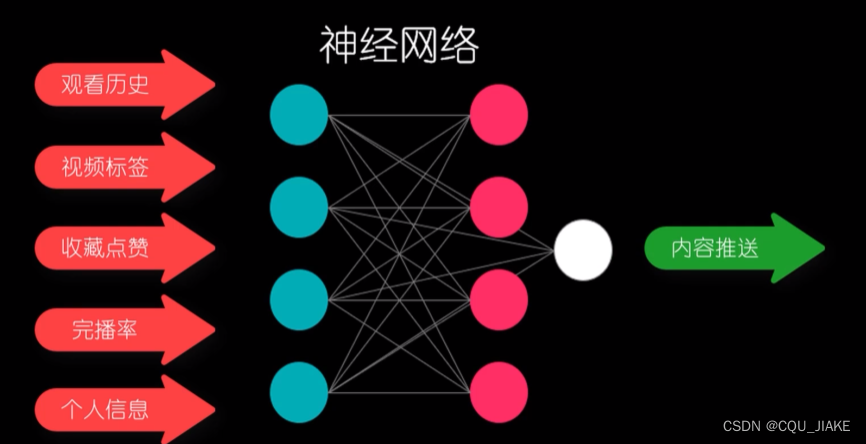
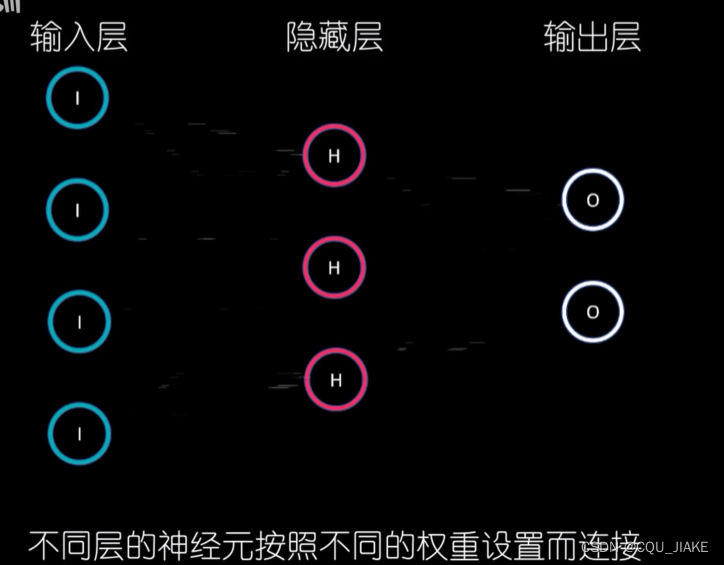
输入层




隐藏层






存在一个阈值,如果低于某一阈值就不激活;高于了就激活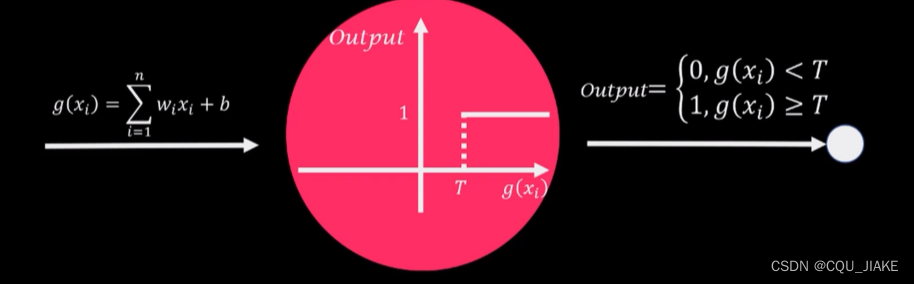



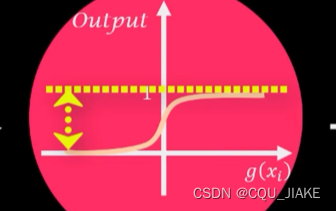
输出层


逆向参数调整方法



初始阶段,随机设置权重值w1,w2
依据训练集
两个数学方法 (梯度下降、链式法则)
调参借助两个数学方法






![]()

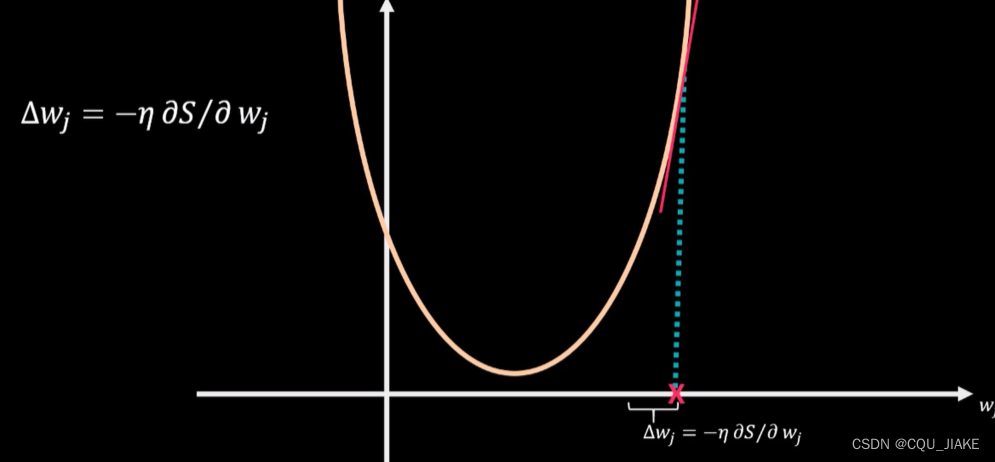




当导数为负时,步幅为正

就是说,这个调参是建立在预测结果与实际结果基础上的;自变量是参数,权重,因变量是反映预测结果与实际间的差距(为误差平方和),目的是要让这个差距最小
就是不同的权重参数下,有不同的误差差距,由此有个参数与误差间的函数;然后依据每点参数下的导数,去逐渐调整参数权值w;
当导数为负时,说明此时增大权值会使误差减少;当导数为正时,此时增大权值会使误差增大;故应始终朝使误差减少的方向,所以调整步幅要与导数方向相反
然后还有一个学习因子,表示基于当下参数的导数下,一个恒定的学习步幅,因子越大,那么调整的幅度越大;



在求导过程中会用链式法则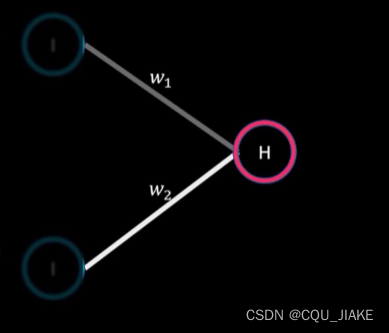

就是求导是求误差与参数间的关系,误差与神经网络产生的输出有直接关系,与参数无直接关系;产生的输出与隐藏层的激励函数有直接关系,是sim函数(即g函数),sim与权值设置w有直接关系,由此是链式法则
这里是省略了隐藏层,就是隐藏层直接就是输出层,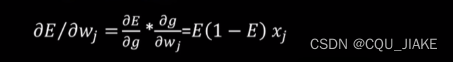
可以发现是有这样一步的,g就是隐藏层汇总的信息,w是从输入层到隐藏层的汇总
E对g求偏导的结果、形式应该是固定的
对于汇总输入信号到隐藏层中的求导过程,是对wj求偏导,也就是只去确定一个权值,这就自动忽略了其他神经元对这个隐藏层神经元的影响,即其他权值wi(i不等于j)对这个路径无影响
是输入层接受输入,然后对各个隐藏层产生权值和积累,最后每个隐藏神经元会积累的权值和为gx
x是最开始的直接输入,隐藏神经元会依据其所接受的信号强度,产生它的激励,即E函数,作为这个隐藏层神经元的输出,有输出就会和最终结果有差距,就会产生S
所以就是
x->g->e->s
x依据各个输入层之间的神经元权重分配,分配给相应的隐藏层
多层
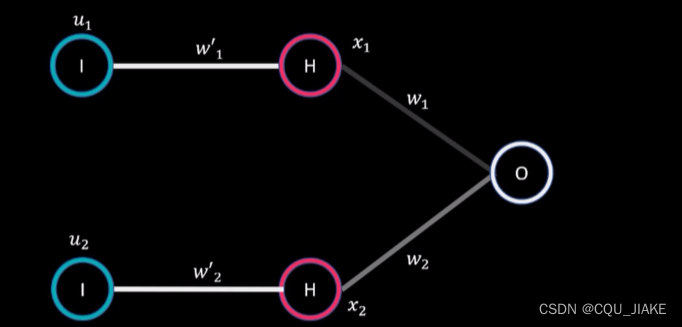

 就是说,e对xj求偏导是体现的输出层对其紧邻的单个隐藏层神经元的关系,是紧邻的单个隐藏层神经元到它的路径,它有权值为w1,w2,这要确定就是确定w1,w2,确定好这个以后再往前回去推更前一层的权值,也就是说在更上一层时,w1,w2就已经成为了常数
就是说,e对xj求偏导是体现的输出层对其紧邻的单个隐藏层神经元的关系,是紧邻的单个隐藏层神经元到它的路径,它有权值为w1,w2,这要确定就是确定w1,w2,确定好这个以后再往前回去推更前一层的权值,也就是说在更上一层时,w1,w2就已经成为了常数
e对xj求偏导是第j个最里层隐藏层对输出层的影响,然后xj对wi'求偏导,是外面一层的所有神经元中的第最里层的第i个对第j个下层隐藏层的影响,是隔离了其他外层神经元的影响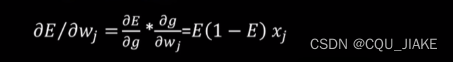
最终要建立的是,最后的误差与各个神经元连接之间的直接函数关系与导数关系,依据的就是这个神经元到最后最终输出所经过的神经元路径的链式法则来确定
要确定w1,就是它到最后输出只有一条路,所以只有少量的链式法则;对于w1',要在递归上w1
对于步骤5,S是误差,E是最终输出,确定xj参数
输出由参数以及输入所确定,是一个二元的,所以即使在只有一层时,也是偏导,即在一层时,是保证统一输入来去调整参数;
在这里,是先确定好最里层的参数,然后就是保证参数不变,去依据外层的参数w'的变化使这里输入发生变化,所以是变成了对里层隐藏层的输入x求偏导,,而不是其到输出层的参数w求偏导
然后里层隐藏层的输入受限于外一层隐藏层,然后依次确定这个连接的参数w',就是对其求偏导,就是控制上一层的输入不变,调整其参数w',因为就是要去确定这个参数w',也就是链式法则的最底层
如果它不是最底层,就是要保证这个参数w'在后续不会再发生变化,从而在这一层链式法则中,求偏导不是对参数w'求,而是对这个外层神经元的输入去求偏导,然后在那个外层神经元基础上去继续求偏导,直到找到要确定的参数的位置,即那个参数引起后续联通其到输出层神经元路径上的所有其他神经元变化
即,如果有多层,那么就有多次的链式法则,但只有一个w参数,这个参数是在最后的链式法则,就是这个w影响了其后续所有的神经元输入值的变化,然后中间过程的求偏导,都是对该神经元的输入求偏导,而不是对其与输出层所联通的权值w求偏导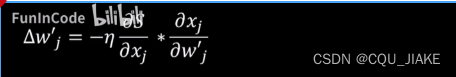
对于上层隐藏层通过路径w对下层隐藏层造成的影响求偏导,其结果都满足 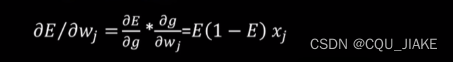
注意应当是紧邻的输入与输出层的关系,就是直接这个输入,在对于权值w下,直接对其相连的神经元造成的影响,是这样,是由于选取的激励函数g函数是sim函数所决定的形式;然后最后要固定输入,定权值的影响,所以xj就是常量,在求导结果表达式当中
里层神经元与上一层单个神经元,由权值与其输入共同决定,还需要注意,里层不仅与这个相连,与其他的都相连,只是在对单个xj,或wj求偏导后,其他的都直接为0没了
E是这个里层神经元最后产生的输出,xj是外层神经元所接受的信号, 要知道权值的影响,就是对权值求偏导
对权值求偏导,那么输入就作为常数体现在最后的影响里;对输入求偏导,那么权值参数就作为常量体现在最后的影响里

![]()
u是最原始输入,w是第一层输出,x是第二层输出,e是最终输出层
就是说我们要得到的是在特定训练集下,参数与其所产生的预测误差之间的差距的导数,
既然是特定训练集,那么原始输入可以视为常数,因为要调整的是参数w,自变量是w
要注意的是,w是两层神经元连接的权重
这个式子里的j,是说要确定多个与输出层连接的隐藏层之间的权重,要确定是要一个一个的确定


![]()
![]()
数学总结理解
就是说,激励函数是确定每层神经元递归下去时所带的一项,就是描绘的输入与输出之间的递归变化关系,sig函数是x(1-x)w,(对应是里层输出x,以及参数w不变,输入边)
每递归一层,就会多一个这样的形式,这样的形式由激励函数所确定,就是求导求出来的
然后还有2(E-y),这个是由最外面的梯度下降的检验方式,即误差平方所决定的,每个表达式里都有,而且唯一