理顺 QR 分解算法

news2025/1/18 9:48:41

咱们网站的这个公式编辑器，估计是后台生成图片后贴回来的，固定分辨率而且分辨率不高。

还不如先离线 latex 生成 pdf 后再截图上来

1. Why QR

When A and b are known, to solver the minimization of $|| Ax - b ||_{2}$ , where $A \in \mathbb{R}^{m\times n}, b \in \mathbb{R}^{m}, and\,\,m \ge n$ .

The reduction of A to various canonical form via orthogonal transformations should use Householder reflections and Givens rotations.

2. preview on orthogonal matrix

2.1 Orthogonal matrix

$\mathbf{Q} \in \mathbb{R}^{m\times m} , \,\mathbf{Q} \,$ is orthogonal matrix, if:

$\mathbf{Q}^{\mathbf{T}}\mathbf{Q}=\mathbf{Q}\mathbf{Q}^{\mathbf{T}}=\mathbf{I}_{m}$

2.2 rotation matrix is orthogonal matrix

$\mathbf{Q} = \left( \begin{array}{cc} \,\,\,\,\,\cos(\theta) & \sin(\theta)\\ -\sin(\theta)& \cos(\theta)\\ \end{array} \right)\\$

$\mathbf{Q}$ is orthogonal and $\mathbf{Q}$ is a rotation matrix.

If $y = \mathbf{Q}^\mathbf{T}x$ , then $y$ is obtained by rotating $x$ counterclockwise through an angle $\theta$ .

2.3 reflection matrix is orthogonal matrix

$If\\ \mathbf{Q} = \left( \begin{array}{cc} \cos(\theta) & \sin(\theta)\\ \sin(\theta) & -\cos(\theta)\\ \end{array} \right)$

$\mathbf{Q}$ is orthogonal and $\mathbf{Q}$ is a reflection matrix.

If $y = Q^Tx = Qx$ , then $y$ is obtained by reflecting the vector $x$ across the line defined by

$\mathbf{S}=\mathbf{span}\left\{\left[ \begin{array}{c} \cos(\theta/2)\\ \sin(\theta/2)\\ \end{array}\right]\right\}$

That means $\overrightarrow{x}$ and $\overrightarrow{y}$ are axial symmetry by S,

x is the preimage, y is the image, S is the mirror surface.

looks like :

%input x, ta = theta

%x = [-sqrt(2)/2.0, sqrt(2)/2.0]
x = [1; 1;]
ta = pi/5

S = [cos(ta/2.0), sin(ta/2.0)]
Q = [cos(ta), sin(ta); sin(ta), -cos(ta);]

y = Q*x

figure;
%1. draw axis
xmin = -2
xmax = 2
ymin = -2
ymax = 2

axisx = xmin:xmax;
axisy = zeros(size(axisx));
plot(axisx, axisy, 'k--', 'LineWidth', 0.7); % Plot x=0 axis
hold on;
plot(axisy, xmin:xmax, 'k--', 'LineWidth', 0.7); % Plot y=0 axis
hold on;

%2. draw surface of mirror
sx = -2*S(1):0.5:2*S(1)
sy = (S(2)/S(1))*sx
plot(sx, sy)
text(sx,sy, 'S')
hold on;

%3. draw preimage
plot(x(1), x(2), 'ro')

text(x(1)+0.1, x(2)+0.1, 'x')
hold on;

%4. draw image
plot(y(1), y(2), 'bo')
text(y(1)+0.1, y(2)+0.1, 'y')

%5. axis label
xlabel("X")
ylabel('Y')
v=[xmin, xmax, ymin, ymax]
axis(v)
%axis on

3. Householder transformation

In section 2, the reflection is introduced from the mirror surface. But, in this section, it is introduced from normal direction.

Let $\vec{x} \in \mathbb{R}^m,and \,\, \vec{x} \ne \vec{0}$

$\beta = \frac{2}{v^Tv}\\\\ \mathbf{P} = \mathbf{I}-\beta v v^T$

then $\mathbf{P}$ is

a $Householder\,\,reflection$

or $Householder\,\, matrix$

or $Householder\,\,transformation$

which are synonyms.

And $v$ is the $Householder vector$ .

When $y = \mathbf{P}x$

$y$ is the image from $x$ by reflecting with the hyuperplane $\mathbf{span}\{v\}^\perp$ and the mirror surface is cross the $O$ point.

$\mathbf{3\,\, properties \,\, of\,\,\mathbf{P}:}$

$\mathbf{P} \,\,is\,\, symetric,\, \mathbf{H}^\mathbf{T} = \mathbf{H};$

$\mathbf{P}\,\, is\,\, orthogonal,\, \mathbf{H}^{-1} = \mathbf{H};$

$If\,\, \mathbf{A} \,\,is\,\, symetric,\, then\,\, \mathbf{A}_1 = \mathbf{P}^{-1}\mathbf{A}\mathbf{P} = \mathbf{P}\mathbf{A}\mathbf{P} \,\,is\,\, symetric.$

$\mathbf{Calculate\,\, the\,\, } Householder\,\, matrix:$

If $x \in \mathbb{R}^n\,\, and\,\, y \in \mathbb{R}^n, \parallel x\parallel _2 = \parallel y\parallel _2$

let $w=\frac{x-y}{\parallel x-y\parallel _2}$ (this is the normal direction)

$\mathbf{H} = \mathbf{I} - 2ww^\mathbf{T} = \mathbf{I} - 2\frac{(x-y)}{\parallel x-y\parallel _2^2} (x^\mathbf{T} - y^\mathbf{T})$

then $\mathbf{H}x = x -(x-y) = y$ ;

约化定理：

Let $x=(x_1, x_2, ... ,x_n)^T \ne \mathbf{0}$ ,

then $\exists \mathbf{P}$ st. $\mathbf{H}x = -\sigma {e}_1$

and:

$\left\{\begin{array}{l} \mathbf{H} = \mathbf{I}-\beta^{-1}uu^T\\ \sigma=sgn(x_1) {\parallel {x} \parallel}_2;\\ u=x+\sigma e_1;\\ \beta = \frac{1}{2}\parallel u \parallel _2^2 = \sigma(\sigma+x_1) \end{array} \right.$

约化定理毕；

约化定理example：

Let $x = (3,5,1,1)^T$ then $\parallel x \parallel _2 = 6$ , and $\sigma = 6$

to calculate $u$ :

$u = x - \sigma e_1 = (9, 5, 1, 1)^T$

then

$\parallel u \parallel_2^2 =108, \beta = \frac{1}{2}\parallel u \parallel_2^2 = 54$

$\mathbf{H} = \mathbf{I} - \beta^{-1}uu^T\\ \\=\mathbf{I} - \beta^{-1}\left[ \begin{array}{cccc} 81 & 45 & 9 & 9\\ 45 & 25 & 5 & 5\\ 9 & 5 & 1 & 1\\ 9 & 5 & 1 & 1 \\ \end{array} \right]\\ \\\\= \frac{1}{54}\left[ \begin{array}{cccc} -27 & -45 & -9 & -9\\ -45 & 29 & -5 & -5\\ -9 & -5 & 53 & -1\\ -9 & -5 &-1 & 53\\ \end{array} \right ]$

$y = \mathbf{H}*x \\= \left[ \begin{array}{c} -6.0000e+00\\ 1.7764e-15\\ 4.2327e-16\\ 4.4409e-16\\ \end{array} \right]$

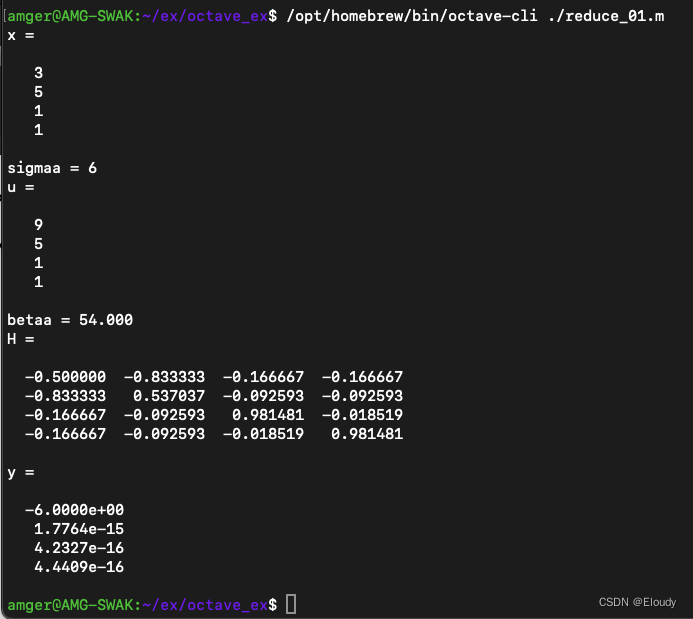
Here is the matlab code:

reduce_01.m:

x=[3;5;1;1;]
sigmaa =sign(x(1))*norm(x)
u = x+sigmaa*eye(4)(:,1)
betaa = 0.5*(norm(u))^2
H = eye(4) - (1.0/betaa)*u*u'
%debug
%h=betaa*H

y = H*x

未完待续 ... ...

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1416494.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！