-
通信原理第17页第一段:
例如, s ( t ) = 8 s i n ( 5 t + 1 ) , − ∞ < t < ∞ s(t)=8sin(5t+1),-\infty<t<\infty s(t)=8sin(5t+1),−∞<t<∞,就属于周期信号,其周期 T 0 = 2 π / 5 T_0=2\pi/5 T0=2π/5
三角函数很多都忘光了,回忆下三角函数的基本特性
原型: y = A s i n ( ω x + φ ) 原型:y=Asin(\omega x+\varphi) 原型:y=Asin(ωx+φ)
其中 A A A 为振幅, ω \omega ω 为角频率(单位:弧度/秒,rad/s), φ \varphi φ 为初始相位
T = 2 π ω = 1 f f = 2 π ω T=\frac{2\pi}{\omega}=\frac{1}{f}\\ f=2\pi\omega T=ω2π=f1f=2πω
其中 T T T 为周期, f f f 为频率,其中 2 π 2\pi 2π 表示一个单位圆的周长,以角频率 ω \omega ω 的速度绕圆心转动,则需要 T T T 时间转完一圈,而频率表示 1 s 1s 1s 内转完一圈的次数,就是频率 f f f 了,单位赫兹 H z Hz Hz

-
通信原理第17页最后一段:
若信号电压和电流的值随时间变化,则 S S S 可以改写为时间 t t t 的函数 s ( t ) s(t) s(t)。故 s ( t ) s(t) s(t) 代表信号电压或电流的时间波形。这时,信号能量 E E E 应当是信号瞬时功率的积分:
E = ∫ − ∞ ∞ s 2 ( t ) d t E=\int^{\infty}_{-\infty}{s^2(t)dt} E=∫−∞∞s2(t)dt
其中 E E E 的单位时焦耳(J)
因为工程应用中常用的是电压,比如 TTL 电平标准,+5V 表示逻辑 1,0V 表示逻辑 0,所以这里以电压 V V V 来举例
若单位时间内电压不变,通过 1 Ω 1\Omega 1Ω 的电阻,电压的变化函数 V = 5 V=5 V=5,它的功率非常好求,就是电压的平方 V 2 d t V^2dt V2dt,等于 5 2 d t = 25 d t 5^2dt=25dt 52dt=25dt
若单位时间内电压变化,可用 V = s ( t ) V=s(t) V=s(t) 函数来表示电压随时间变化,则需要对 s 2 ( t ) s^2(t) s2(t) 进行积分,就有了上面的公式

-
通信原理第18页开头:
若信号的能量是一个正的有限值,即
0 < E = ∫ − ∞ ∞ s 2 ( t ) d t < ∞ 0<E=\int^{\infty}_{-\infty}s^2(t)dt<\infty 0<E=∫−∞∞s2(t)dt<∞
则称此信号为能量信号。例如,第 1 章中提到的数字信号的一个码元就是一个能量信号。现在,我们将信号的平均功率定义为
P = lim T → ∞ 1 T ∫ − T / 2 T / 2 s 2 ( t ) d t P=\lim_{T→\infty}\frac{1}{T}\int^{T/2}_{-T/2}s^2(t)dt P=T→∞limT1∫−T/2T/2s2(t)dt
能量信号的平均功率 P = 0 P=0 P=0, 因为上面这个式子表示若信号的能量有限,则在被趋于无穷大的时间 T T T 去除后,所得平均功率趋近于零 -
两个公式主要是在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 上对整个信号的总能量,以及平均到每个单位时间 d t dt dt 上的功率大小,来分析的
-
能量信号:比如在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 内只发送了一个码元
从总能量来看:对 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 积分,根据分段积分法,对 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 积分其实就是对 ( − t 0 , t 0 ) (-t_0,t_0) (−t0,t0) 积分,恒为一个有限的正值
从平均功率来看:对 ( − t 1 , t 1 ) (-t_1,t_1) (−t1,t1) 积分,总能量不变,但是除以 2 t 1 2t_1 2t1,除的区间变长了,本来是除以 2 t 0 2t_0 2t0 的,那么每个 d t dt dt 积分出来的结果就又变小了,再拓展到 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞),那么 d t dt dt 积分出来的结果就趋近于零了
具有这种性质的信号,就称之为能量信号,即总能量是一个正的有限值,但平均功率等于零

-
功率信号:比如在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 内发送持续的广播信号
从总能量来看:对 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 积分,积分的结果无穷大,因为信号在 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 没有边界嘛,面积也就无穷大
从平均功率来看:对 ( − ∞ , + ∞ ) (-\infty,+\infty) (−∞,+∞) 积分得到总能量无穷大,对 d t dt dt 积分出来的结果都为一个恒定正值
具有这种性质的信号,就称之为功率信号,即总能量趋近于无穷,但平均功率等于恒定的正值

确知信号的类型:能量信号与功率信号
news2026/2/17 1:29:41
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1416311.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
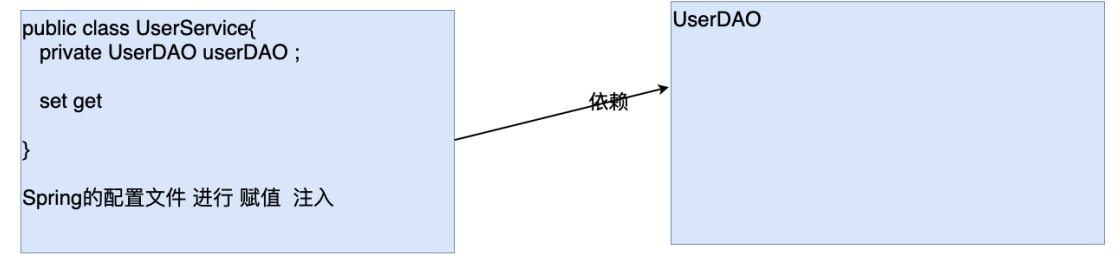
Spring5深入浅出篇:Spring中ioc(控制反转)与DI(依赖注入)
Spring5深入浅出篇:Spring中ioc(控制反转)与DI(依赖注入)
反转(转移)控制(IOC Inverse of Control)
控制:对于成员变量赋值的控制权
反转控制:把对于成员变量赋值的控制权,从代码中反转(转移)到Spring⼯⼚和配置⽂件中完成好处:…
docker 部署xxl-job
docker 部署xxl-job
XXL-JOB github地址 https://github.com/xuxueli/xxl-job
XXL-JOB 文档地址 https://www.xuxueli.com/xxl-job/
XXL-JOB是一个分布式任务调度平台,其核心设计目标是开发迅速、学习简单、轻量级、易扩展。现已开放源代码并接入多家公司线上产品…
Ubuntu apt update提示:GPG 缺少公钥解决方法
Ubuntu 运行:
sudo apt update
#or
sudo apt-get update提示:GPG 缺少公钥以及404 Not Found,如下面所示,有mirror.bwbot.org 和ppa.launchpadcontent.net两个源出现问题。 好多网友用后面的方法解决 真正解决:gpg --verify sig:…
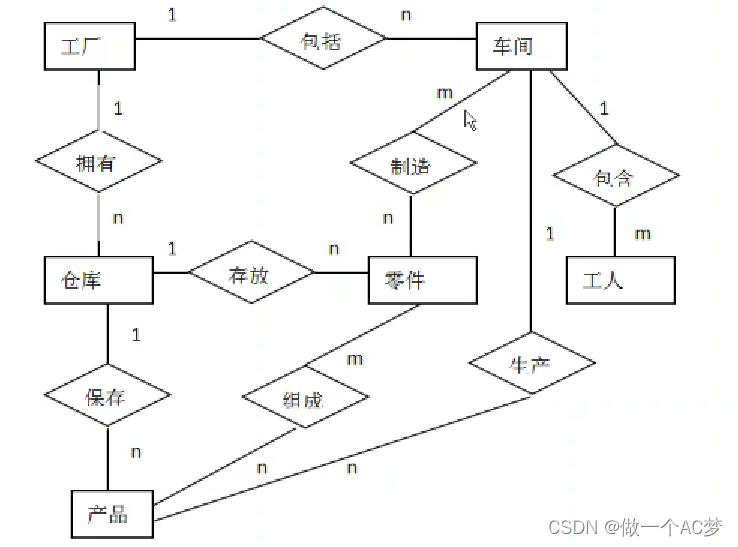
数据库ER图相关概念及其画法
ER图基本概念 ER图(Entity-Relationship Diagram)是一种用于描述现实世界概念模型的图形化表示方法,通过使用图形符号和元素来表示实体、属性和它们之间的关系。在ER图中,实体、属性和关系分别使用不同的图形元素来表示࿰…
【前端web入门第二天】01 html语法实现列表与表格_合并单元格
html语法实现列表与表格
文章目录: 1.列表 1.1 无序列表1.2 有序列表1.3 定义列表 2.表格 2.1 表格基本结构2.2 表格结构标签2.3 合并单元格 写在最前,第二天学习目标: 列表 表格 表单 元素为嵌套关系 1.列表
作用:布局内容排列整齐的区域。 列表分类:无序列表、有序列表…
Redis中BigKey的分析与优化
Redis中BigKey的分析与优化
Redis以其出色的性能和易用性,在互联网技术栈中占据了重要的地位。 但是,高效的工具使用不当也会成为性能瓶颈。在Redis中,BigKey是常见的性能杀手之一,它们会消耗过多的内存,导致网络拥塞…
专有钉钉开发记录,及问题总结
先放几个专有钉钉开发文档 专有钉钉官网的开发指南 服务端(后端)api文档 前端api文档 前端开发工具下载地址 小程序配置文件下载地址 后端SDK包下载地址 专有钉钉域名是openplatform.dg-work.cn
开发记录
开发专有钉钉时有时会遇到要使用钉钉的api;通过 my 的方…
【leetcode题解C++】101.对称二叉树 and 111.二叉树的最小深度 and 222.完全二叉树的节点个数 and 110.平衡二叉树
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1: 输入:root [1,2,2,3,4,4,3]
输出:true示例 2: 输入:root [1,2,2,null,3,null,3]
输出:false
思路:…
Pandas.Series.mode() 众数 详解 含代码 含测试数据集 随Pandas版本持续更新
关于Pandas版本: 本文基于 pandas2.2.0 编写。
关于本文内容更新: 随着pandas的stable版本更迭,本文持续更新,不断完善补充。
传送门: Pandas API参考目录
传送门: Pandas 版本更新及新特性
传送门&…
Blender教程(基础)-物体添加-03
1、打开的界面如下图会存在3个物体、英文状态下按键盘字母A全选、然后按键盘delete删除。 删除后一片空白 2、新增物体 方式1:在英文状态下按键盘shiftA组合键弹出如下添加物体弹窗 方式2:在菜单下找到添加点击弹出添加选项 3、举例新增物体 采用上述…
MongoDB本地部署并结合内网穿透实现公网访问本地数据库
文章目录 前言1. 安装数据库2. 内网穿透2.1 安装cpolar内网穿透2.2 创建隧道映射2.3 测试随机公网地址远程连接 3. 配置固定TCP端口地址3.1 保留一个固定的公网TCP端口地址3.2 配置固定公网TCP端口地址3.3 测试固定地址公网远程访问 4. 结语 前言
MongoDB是一个基于分布式文件…
Gin 应用多实例部署session问题、session参数与刷新
文章目录 一、Gin Session 存储的实现方案二、memstore:基于内存的实现2.1 基本使用2.2 关键参数 三、使用redis:多实例部署3.1 使用redis优势3.2 基本使用 四、信息安全的三个核心概念五、Gin Session 参数5.1 参数介绍 六、Session 自动刷新 一、Gin S…
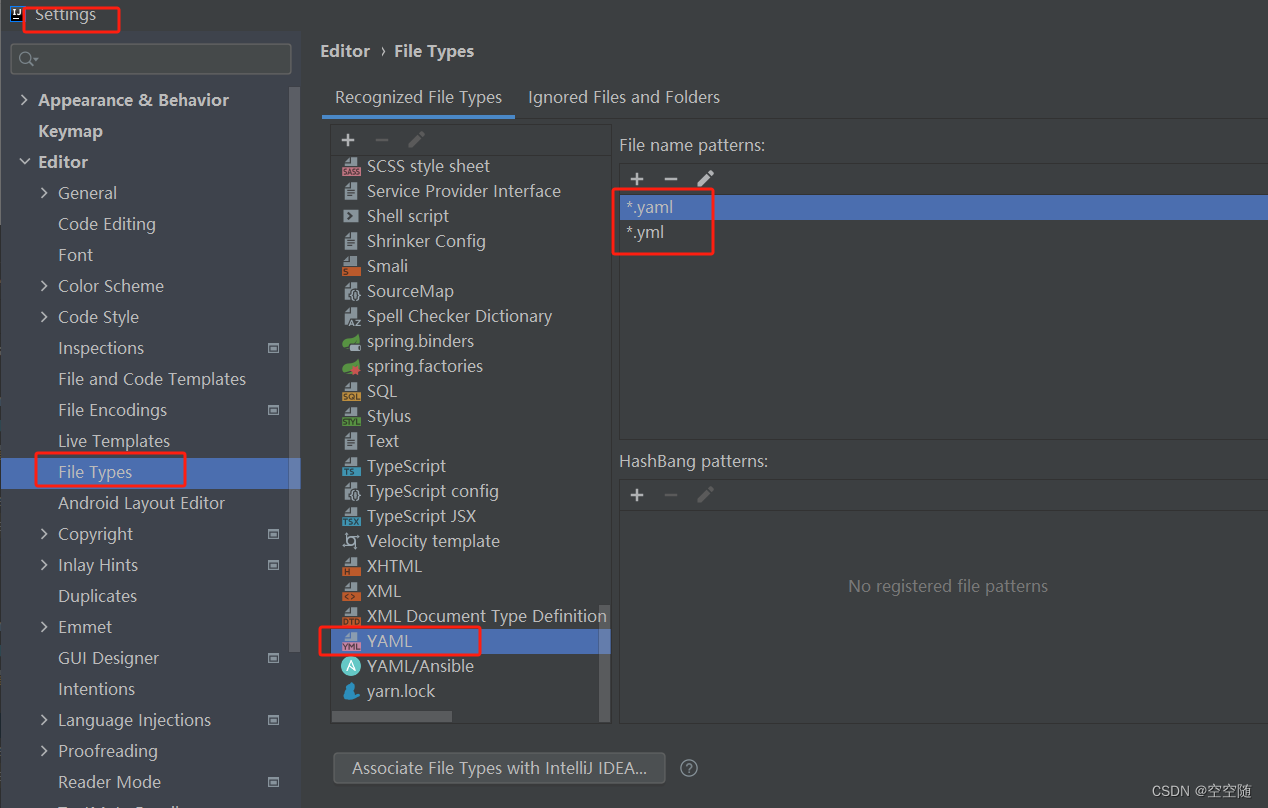
idea中yml文件没有提示解决办法
两步解决yml文件不显示提示,yaml文件显示提示问题
1、在插件中心,先下载下图两个插件 2、在Editor》File Types新增文件类型,文件名匹配规则需要将yaml和yml的都加上,加好之后,重启idea,即刻生效。
《汇编语言:基于linux环境》eatsyscall汇编程序
当阅读此书,作者编写了一个这样的程序,我也想试一下。照着书中的代码写了下,可以使用nasm正常编译,ld也可以正常链接,但是无法正常执行。总是报错。
; nasm -f elf64 -g -F stabs eatsyscall.asm
; ld -o eatsysca…
CTF CRYPTO 密码学-6
题目名称:敲击
题目描述:
方方格格,不断敲击 “wdvtdz qsxdr werdzxc esxcfr uygbn”
解题过程:
step1:根据题目描述敲击,wdvtdz对应的字符为x step2:依此类推r,z,o&…
张维迎《博弈与社会》笔记(4)导论:社会最优与帕累托标准
本节我们将从社会的角度来评判人类行为:一个社会应该采取什么样的标准来判断个人行为?具体地讲,我们需要知道,从社会的角度来评判,什么样的行为是正当的,什么样的行为是不正当的;什么样的行为应…
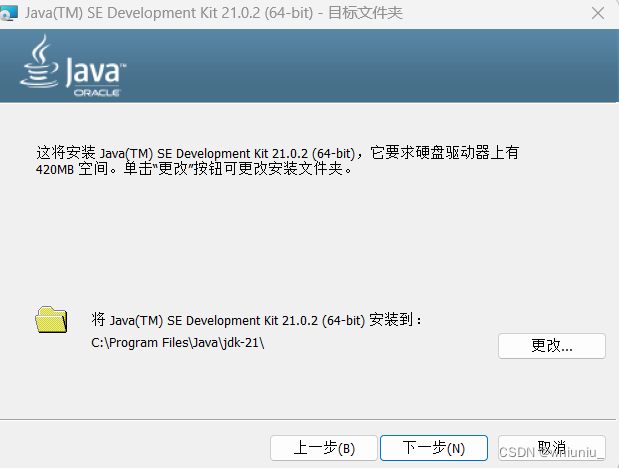
安装 java 的 JDK
前几天重装系统以后想起来要重装 java 的JDK
安装地址 Windows 下的 JDK 数据包有三种可选的下载:Windows x64 Compressed Archive、Windows x64 Installer 和 Windows x64 MSI Installer。其中,前者为 JDK 的免安装版本,后两者均为 JDK 的离…
05-Nacos-配置中心接入
1、pom依赖
<dependency><groupId>com.alibaba.cloud</groupId><artifactId>spring-cloud-starter-alibaba-nacos-config</artifactId></dependency>
2、配置文件
spring:application:name: nacos-config## 当前环境,这个和…
【JS基础】事件对象event、环境对象this、事件的高级操作
文章目录 一、事件对象1.1 事件对象是什么?1.2 使用方法 二、环境对象this以及回调函数2.1 它是什么?2.2 演示示例 三、事件的高级操作3.1 事件流3.2 事件捕获3.3 事件冒泡以及阻止冒泡3.4 事件解绑3.5 mouseover和mouseenter事件的区别3.6 事件委托它是…
架构篇21:高性能负载均衡-算法
文章目录 轮询加权轮询负载最低优先性能最优类Hash 类源地址 HashID Hash小结负载均衡算法数量较多,而且可以根据一些业务特性进行定制开发,抛开细节上的差异,根据算法期望达到的目的,大体上可以分为下面几类。 任务平分类:负载均衡系统将收到的任务平均分配给服务器进行处…