题目

题目链接

分析

读完本题以及结合题目给出的图我们可以很直观的看到，这道题目是让我们求形成凹槽的面积。

我们可以针对每一个数字形成凹槽的面积进行计算，然后相加数组每一个数字形成凹槽的面积即可。

那么问题来了，怎么知道一个数字是否可以形成凹槽，以及计算形成凹槽的面积。

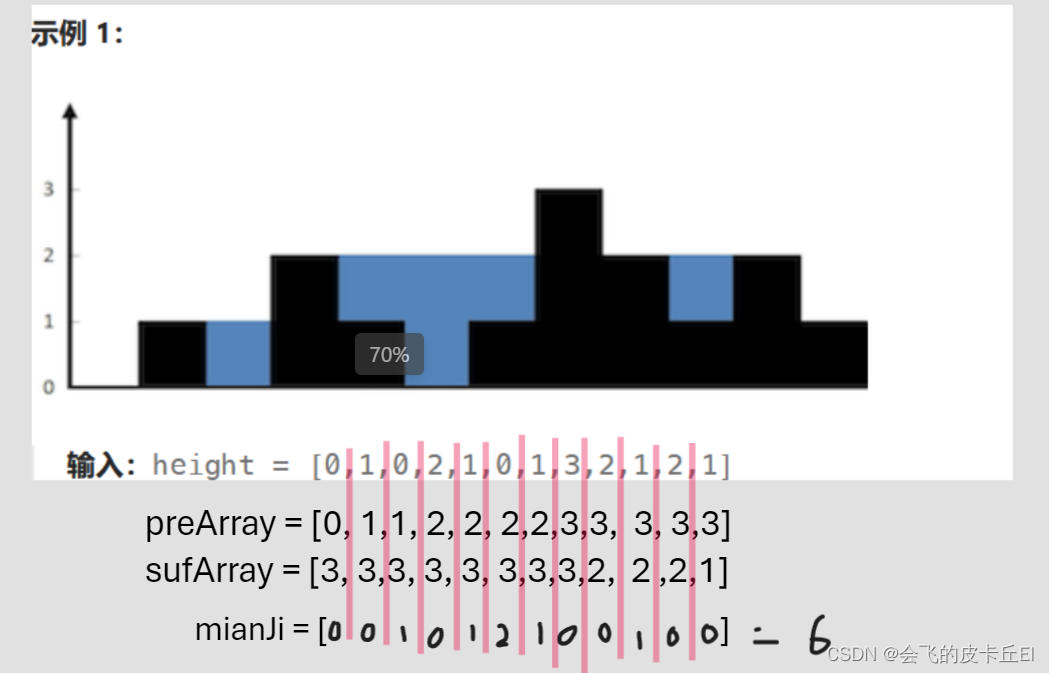
要想形成凹槽，就必须知道左右两边的最大数，如下图中，1 的左边最大值为2，右边最大值为3，那么针对这个1形成的凹槽面积就是 ：min(左边最大值,右边最大值) - height[i]利用上面的规则，我们将会得到一个 preArray 数组 和 sufArray数组，preArray 数组这个数组记录每一个数字的左边的最大值，sufArray数组这个数组记录每一个数字的右边的最大值。
下图我展示了 preArray 和 sufArray 数组，以及每一个元素可以形成凹槽的面积：

代码

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] preArr = new int[n];
        preArr[0] = height[0];
        int[] sufArr = new int[n];
        sufArr[n-1] = height[n-1];
        for(int i = 1;i < n;i ++) {
            preArr[i] = Math.max(preArr[i-1],height[i]);
        }
        for(int i = n - 2;i >= 0;i --) {
            sufArr[i] = Math.max(sufArr[i+1],height[i]);
        }
        int res = 0;
        for(int i = 0;i < n;i ++) {
            res += Math.min(preArr[i],sufArr[i]) - height[i];
        }
        return res;
    }
}

拓展

这道题还可以利用双指针的方法来解答。

定义两个指针 left = 0，right = height.length -1
定义一个前缀最大值 pre_max 和 后缀最大值 suf_max

• 当前缀最大值 < 后缀最大值 时，那么左边木桶的能形成凹槽的面积就是 前缀最大值 - 当前left下标对应的值；然后 left++
• 当前缀最大值 > 后缀最大值 时，那么右边木桶的能形成凹槽的面积就是 后缀最大值 - 当前right下标对应的值；然后 right–
• 当前缀最大值 = 后缀最大值 时，更新left还是right都可以。

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int res = 0;
        int pre_max = 0;
        int suf_max = 0;
        int left = 0;
        int right = n - 1;
        while(left < right) {
            pre_max = Math.max(pre_max,height[left]);
            suf_max = Math.max(suf_max,height[right]);
            if(pre_max < suf_max) {
                res += (pre_max - height[left++]);
            }else {
                res += (suf_max - height[right--]);
            }
        }
        return res;
    }
}