目录
一. 矩阵分解
二. 解方程
三. 例题说明
四. 矩阵的LDU分解
五. 矩阵三角分解的唯一性
一. 矩阵分解
其实我们可以把一个线性系统(Linear System)看成两个三角系统(Triangular Systems),本文章将解释为什么可以这么看待解线性方程组,以及这样理解到底有什么好处。我们知道高斯消元法其实跟矩阵的三角分解有关,如下:
A=LU
其中,A为任意方阵,L为下三角矩阵且对角线处元素均为1,U为上三角矩阵。注意此处的上三角矩阵U的对角线处元素不一定为1.
利用矩阵L和U,可以直接求解Ax=b,该方程也被称之为线性系统。借助矩阵L,也就是正向消元(forward elimination),可以把b变成c。
借助矩阵U,也就是逆向替换(back substitution),可以从c来解x。那么对于任意解方程,我们可以将其标准化为两步,这两部就不需要直接利用A,如下:
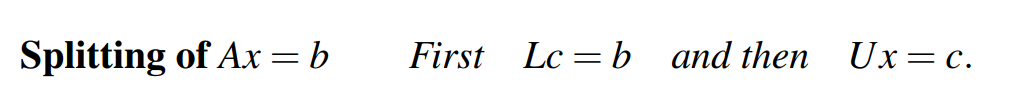
观察第二个方程,两边同时乘以矩阵L,可得:
LUx=Lc
不要忘记A=LU,且Lc=b,也就可得:
Ax=b
说明以上变换是有效的。该方程的思路从理论上是行得通的。
我们都知道三角不等式是很容易解的,相关的elimination code也很容易设计。至于怎么解,我们接着往下看。
二. 解方程
根据以上讨论,我们可以把解方程分成两步。
(1)分解,factor
将矩阵A分解,找到对应的矩阵L与U。
(2)解方程,solve
综合利用L,U和b,确定最终的结果x。
从计算复杂度性的角度来讲,解三角系统的步骤只需要步,因为三角矩阵就只有
个元素,该复杂度性应该比较好理解。
总共有两个三角系统,无论是上三角还是下三角矩阵,复杂性是一样的,只不过解的顺序不同而已。也就是一共步操作即可求解两个三角系统。如果有印象的小伙伴会发现,如果直接从A入手的话,解方程复杂度为:
这也就是通常我们所说的,在不外加任何优化算法的前提下,解线性方程组的计算复杂度为:
三. 例题说明
假定有一个矩阵A,需要解的方程中b=(1,1,1,1),详细的方程如下:
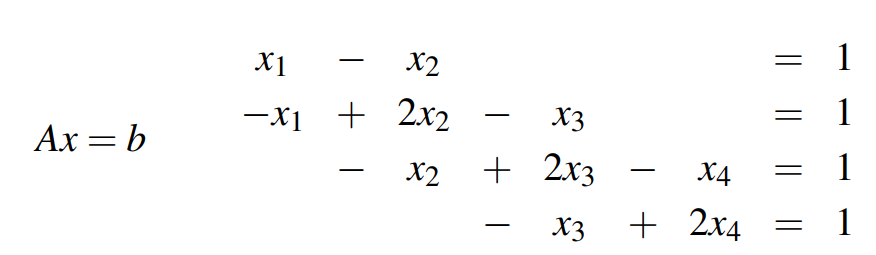
按照以上讨论,我们已知矩阵A和向量b,目标是求解未知向量x。我们的思路是先将其分成Lc=b,接着求解Ux=c。
首先第一步列方程可得:

很容易解该方程,可得对应的c为:
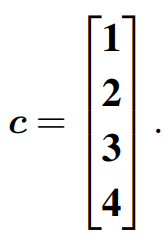
接着列出第二个方程,可得:

求解该方程可得x为:

在这个例子中,系数矩阵中的元素只有1,-1和0,所以解起来会更加简单,之前解方程的复杂度为,那么现在复杂度则只有2n。比如先看第一个方程,Lc=b,我们首先解c1,接着解c2,以此类推,所以这个过程也被称之为正向(forward)求解。
接着解第二个方程Ux=c,是首先解x4,接着解x3,这也就是所谓的逆向求解(backward)。
四. 矩阵的LDU分解
在以上的分析中,其实有一个小问题,我们发现矩阵L和U地位不是均等的。换句话说,矩阵L的对角线处元素均为1,但是矩阵U并不满足此条件。矩阵U对角线处的值均为主元(pivots)。
那么我们能不能让矩阵U的对角线处元素也为1呢?
直接把矩阵U初以主元矩阵D,也就是继续做如下分解:

注意以上是以矩阵每行来理解的,也就是每行均除以对应的di,每个元素都要相应缩减。
当然在我们刚才举的例子中,该矩阵的主元di=1,也就是矩阵D是单位阵:
D=I
但这只是其中的一个例子,在刚才的例题中LU分解与LDU分解的结果是一样的,但仅仅是个例。
一般来讲,矩阵的LU分解与LDU分解往往是不一样的,当然有些地方也会将其称之为LDV分解,只是换个符号而已,本质是一样的。
结合以上,我们可以总结矩阵完整的三角分解(triangular factorization),写做:
A=LDU
该种分解在网路安全等领域很有用,其中矩阵L与U的对角线处元素均为1,D为对角阵也就是矩阵的主元
五. 矩阵三角分解的唯一性
综合以上矩阵的三角分解可以写做LDU或者写做LDV,矩阵U或者叫V的对角线处元素均为1,相当于每行均被主元矩阵D相除。这样的话,矩阵L和U的地位就是一样的。我们来看一个例子。
首先可以将矩阵A进行LU分解,也就是可以得到:
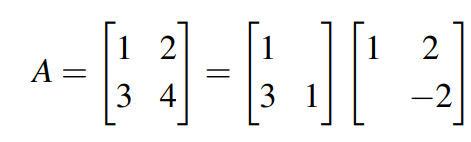
接着可以继续将其LDU分解,可以得到:

很明显可以验证发现矩阵L和U的对角线处元素均为1,矩阵D包含主元1和-2。无论是哪种分解,矩阵L是保持不变的。
很多时候,当我们解释高斯消元法时,都有一定的顺序,但其实这些顺序并不是那么重要,比如就可以利用“Crout algorithm”进行验证。
但是矩阵的LDU分解是唯一的,换句话说:
假定A可以分解成L1D1U1,也就是满足:
同理A可以分解成L2D2U2,也就是满足:
当然以上矩阵L和U均为相应的三角矩阵,且矩阵D 的对角线处元素均不为0,那么可得L,D,U都是对应相等的,也就是:
以上讨论告诉我们无论是LU分解,还是LDU分解,只要矩阵A确定了,那么分解也就确定了。
可以把这种说法,看成一个定理,该定理的证明需要利用逆矩阵,形式比较直接,此处就不啰嗦证明了。