Problem: 208. 实现 Trie (前缀树)

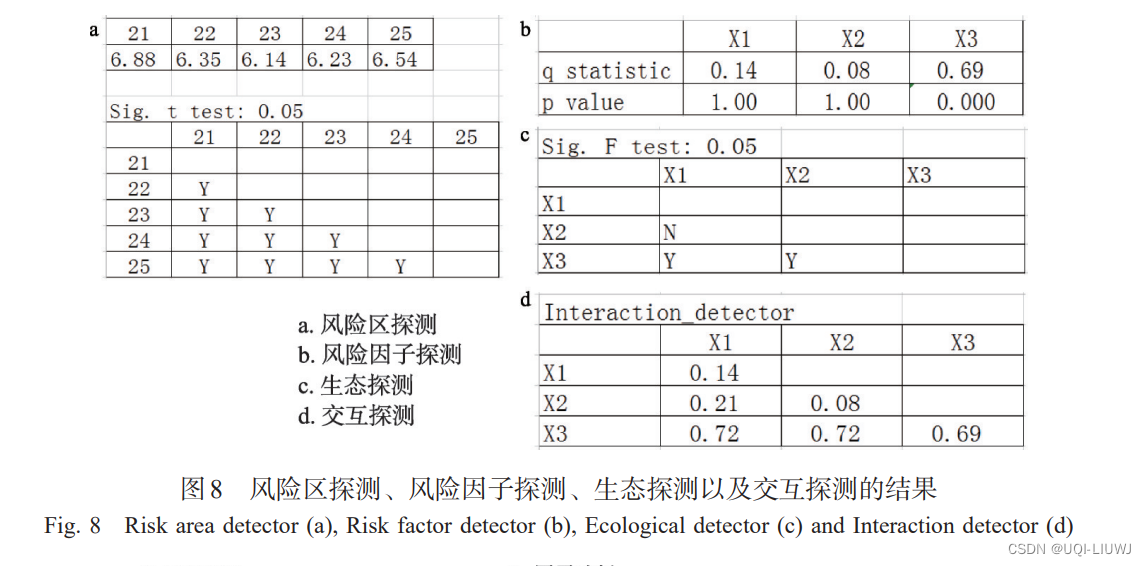
思路

👩‍🏫 宫水三叶

复杂度

💝 TrieNode版

public class Trie
{
	class TrieNode
	{
		boolean end;//标记是否有以当前节点为结尾的字符串
		TrieNode[] ns = new TrieNode[26];
	}

	TrieNode root;

	public Trie()
	{
		root = new TrieNode();
	}

	public void insert(String word)
	{
		TrieNode p = root;
		for (int i = 0; i < word.length(); i++)
		{
			int u = word.charAt(i) - 'a';
//如果正在遍历的该字母在上一个节点的数组坐标中没有记录，就新建一个字母节点在字典树中
			if (p.ns[u] == null)//不存在此节点
				p.ns[u] = new TrieNode();//那就新建节点
			p = p.ns[u];//每一次生成字母都移动指针到下一个字母节点
		}
		p.end = true;// 以当前节点为结尾字符串的个数
	}

	public boolean search(String word)
	{
		TrieNode p = root;
		for (int i = 0; i < word.length(); i++)//枚举所有字符
		{
			int u = word.charAt(i) - 'a';
			if (p.ns[u] == null)//只要有一个字符不存在就 false
				return false;
			p = p.ns[u];
		}
		//最后还要看一下是否以当前字符串结尾
		//例：abcde 路径存在，查 abc，abc存在，但是没有以 c 为结尾的字符串，返回 false
		return p.end;
	}

	public boolean startsWith(String prefix)
	{
		TrieNode p = root;
		for (int i = 0; i < prefix.length(); i++)
		{
			int u = prefix.charAt(i) - 'a';
			if (p.ns[u] == null)
				return false;
			p = p.ns[u];
		}
		//所有字符存在即可，前缀即存在
		return true;
	}
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

💝 二维数组版

//数组版
public class Trie
{
	int N = 100010;
	int[][] trie;
	int[] cnt;
	int idx = 1;

	public Trie()
	{
//		int[i][j] 表示 第 i 行中的 ('a'+j) 是否存在（默认为 0 表示不存在）
		trie = new int[N][26];
		cnt = new int[N];// cnt[i] 记录 格子 i 被标记为结尾的次数
		idx = 1;// 给用到的格子进行编号（从 0 开始避开默认状态）
	}

	public void insert(String word)
	{
		int p = 0;
		for (int i = 0; i < word.length(); i++)
		{
			int u = word.charAt(i) - 'a';
			if (trie[p][u] == 0)
				trie[p][u] = ++idx;
			p = trie[p][u];
		}
		cnt[p]++;
	}

	public boolean search(String word)
	{
		int p = 0;
		for (int i = 0; i < word.length(); i++)
		{
			int u = word.charAt(i) - 'a';
			if (trie[p][u] == 0)
				return false;
			p = trie[p][u];
		}
		return cnt[p] != 0;

	}

	public boolean startsWith(String prefix)
	{
		int p = 0;
		for (int i = 0; i < prefix.length(); i++)
		{
			int u = prefix.charAt(i) - 'a';
			if (trie[p][u] == 0)
				return false;
			p = trie[p][u];
		}
		return true;
	}
}