问题 A: 三五倍数(问题 A: 三五倍数 - BUCTOJ)
思路：这题就暴力，注意一下是小于1000，别取到1000就行。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int sum=0;
for(int i=3;i<1000;i++)
{
if(i%3==0||i%5==0) sum+=i;
}
cout<<sum;
}问题 B: 回文乘积（问题 B: 回文乘积 - BUCTOJ）
思路：我们可以算出所有两个三位数的乘积，然后判回文，再找最大的即可。
#include<bits/stdc++.h>
using namespace std;
int check(int u)
{
vector<int>p;
while(u)
{
p.push_back(u%10);
u/=10;
}
for(int i=0,j=p.size()-1;i<j;i++,j--)
{
if(p[i]!=p[j]) return 0;
}
return 1;
}
int main()
{
vector<int>num;
for(int i=100;i<=999;i++)
{
for(int j=100;j<=999;j++)
{
int mul=i*j;
if(check(mul)) num.push_back(mul);
}
}
sort(num.begin(),num.end());
cout<<num[num.size()-1];
}问题 C: 整除正数（问题 C: 整除正数 - BUCTOJ）
思路：这题我本来想的是暴力，就a,b的最小公倍数就用(a/g)*(b/g)*g（g为最大公因数），但是求模要用乘法逆元，换了好几种写法老是报错，最后发现可以分解质因数。因为质因数可以将每个数凑出来，然后我们对于每个质因数保留次数最高的即可。哦对了，这里质因数我加了一个预处理（线性筛质数）。
#include<bits/stdc++.h>
using namespace std;
bool st[2024]; // st[x]存储x是否被筛掉
vector<int>p;
const int mod=1e9+7;
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) p.push_back(i);
for (auto j:p)
{
if(j>n/i) break;
st[j * i] = true;
if (i % j == 0) break;
}
}
}
map<int,int>mp;
int main()
{
get_primes(2023);
for(int i=2;i<=2023;i++)
{
int t=i;
for(auto j:p)
{
if(t%j==0)
{
int c=0;
while(t%j==0)
{
c++;
t/=j;
}
mp[j]=max(mp[j],c);
}
if(t==1) break;
}
}
int mul=1;
for(auto it:mp)
{
int v=it.first,c=it.second;
for(int i=0;i<c;i++) mul = (long long)mul*v%mod;
}
cout<<mul;
}问题 D: 斐波那契（问题 D: 斐波那契 - BUCTOJ）
思路：这个就递归或者循环都能写，用循环会好一点，递归容易爆栈。
#include<bits/stdc++.h>
using namespace std;
int f[50];
int main()
{
f[1]=f[2]=1;
int n;
scanf("%d",&n);
for(int i=3;i<=n;i++)
{
f[i]=f[i-1]+f[i-2];
}
cout<<f[n]<<endl;
}问题 E: 字串加工（问题 E: 字串加工 - BUCTOJ）
思路：这里显然就是01相邻可以划成一段，连续的0或者连续的1，只能被分进一组，那么找一下字串中有多少符合要求的01位置即可。
#include<bits/stdc++.h>
using namespace std;
int main()
{
string s;
cin>>s;
char c=s[0];
int cnt=0;
for(int i=1;i<s.size();i++)
{
if(c!=s[i])
{
cnt++;
c=s[i+1];//这里要注意一下，因为s[i]相当于已经被划分了
}
else c=s[i];
}
cout<<cnt<<endl;
}问题 F: 有趣的制造（问题 F: 有趣的制造 - BUCTOJ）
思路：这题看似要算一整个区间，但实际上我们可以预处理出来所有符合要求的数，我是用dfs处理的这里一定要预处理到10位数，9位的话1e9是找不到的（是谁因为这里wa了几次我不说）：
void dfs(int u,int fa,int k)
{
if(k>10) return;
int t=fa*10+u;
v.push_back(t);
dfs(3,t,k+1);
dfs(7,t,k+1);
}
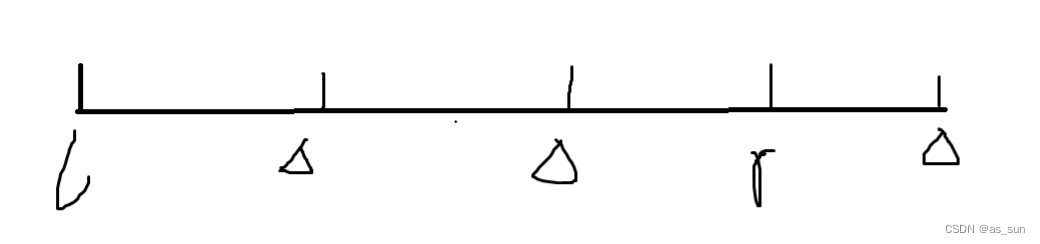
如图，我们可以对预处理出来的数排序，然后找出大于l和大于r的数（如图三角形位置），然后很容易发现每一段区间的结果是同一个值，那么我们可以一个区间一个区间的来算。最后一段注意判断一下，如下：
#include<bits/stdc++.h>
using namespace std;
#define int long long
vector<int>v;
void dfs(int u,int fa,int k)
{
if(k>10) return;
int t=fa*10+u;
v.push_back(t);
dfs(3,t,k+1);
dfs(7,t,k+1);
}
signed main()
{
dfs(0,0,0);
sort(v.begin(),v.end());
v.erase(unique(v.begin(),v.end()),v.end());
//cout<<v.size();
int l,r;
cin>>l>>r;
auto a=lower_bound(v.begin(),v.end(),l);
auto b=lower_bound(v.begin(),v.end(),r);
int ans=0;
for(auto i=a;i<=b;i++)
{
int t=*i;
//cout<<t;
ans+=(min(r,t)-l+1)*(t);//因为r更小的话，区间就只能到r,不能再往后了
l=t+1;//一定要记得更新，因为一段区间算过了后面的值跟前面那段区间就没什么关系了
}
cout<<ans;
}问题 G: 流吧！我的眼泪（问题 G: 流吧！我的眼泪 - BUCTOJ）
思路：这里要找m的最小值，同时要保证所有的杯子都装满，那么就是二分的题。我们很容易去获取m的范围[1,max(a)]，然后结果一定在这个里面，我们就去二分查找即可。
#include<bits/stdc++.h>
using namespace std;
int a[2000010],n,m;
int check(int k)
{
int c=0;
for(int i=1;i<=n;i++)
{
c += ceil(a[i]*1.0/k);
}
if(c<=m) return 1;
else return 0;
}
int main()
{
scanf("%d%d",&n,&m);
int mx=0;
for(int i=1;i<=n;i++) scanf("%d",&a[i]),mx=max(mx,a[i]);
int l=1,r=mx;
while(l<r)
{
int mid=(l+r)/2;
if(check(mid)) r=mid;
else l=mid+1;
}
cout<<l<<endl;
}问题 H: 再会，谢谢所有的鱼（问题 H: 再会，谢谢所有的鱼 - BUCTOJ）
思路：这里如果只有一个区间的话就很简单，就是求给定长度区间的和的最大值，可以用前缀和+暴力枚举，也可以用滑动窗口，但是这里求的是两段区间而且不重合。那么就要再想想了，很明显最关键的地方在于不能重合，而我们暴力每次也只能确定一个端点的值，故而可以暴力枚举出一个区间的左端点，那么右端点在它左边的区间一定可以和它同时被选，所以我们就这样来考虑，对于每个点预处理它左边所有长为k的区间的和的最大值，然后以这个点作为下一个区间的左端点，往后延伸k，求出和，两者相加就是这个点能得到的最大值，将所有的点都考虑一下即可。
另外，这里一定要注意，是有负值的，所以对于要找最大值的地方，赋初值的话一定要小于所有可能的值（我可不说是谁因为初值赋大wa了三四次，哎！）
#include<bits/stdc++.h>
using namespace std;
int a[200010];
long long s[200010],p[200010];
signed main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,k;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),p[i]=-1e18;
s[0]=0ll;
for(int i=1;i<=n;i++) s[i]=s[i-1]+(long long)a[i];
long long mx=-1e18;
for(int i=k;i<=n;i++)//枚举右端点，取等
{
p[i]=max(p[i-1],s[i]-s[i-k]);
}
for(int i=n-k;i>=k;i--)
{
mx=max(mx,s[i+k]-s[i]+p[i]);
}
cout<<mx<<endl;
}
}问题 I: 木头加工（问题 I: 木头加工 - BUCTOJ）
思路：切割方案最小，那么每一段都要尽可能地长，那么就是找所有木头的最大公因数。
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
scanf("%d",&n);
int l=0;
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
l=__gcd(l,x);
}
cout<<l;
}问题 J: 进阶斐波那契（问题 J: 进阶斐波那契 - BUCTOJ）
思路：这道题显然不能再暴力求解了，这里其实是一种类型的题，快速幂+矩阵优化求斐波那契数列。虽然这里要求的是平方和，但是平方和有一个性质：
f1^2+f2^2+...=f[n]*f[n+1]
所以这里我们实际上只用得到f[n-1]和f[n]就可以了，但是n直接干到1e18，有点大了，然后就要引入刚刚说的快速幂+矩阵优化求斐波那契数列。
ps:笔快没墨了，将就看一下。
按照上面的很容易可以发现，我们可以用矩阵乘法求出f[n]和f[n+1],但是这里的话就是是n-1次方了，有点大，所以引入快速幂优化。
快速幂优化实际就是二进制思想：
求3^11=3^8*3^2*3^1将11拆成8+2+1,
实现的话差不多是下面这样：
int k=11
int a=3;
while(k)
{
if(k&1) ans *= a;
a*=a;
k>>=1;
}
所以我们只用把后面n-1次方的部分算出来，然后再跟前面的相乘，就可以得到f[n],f[n+1]了，它们相乘就是结果。
实现如下：
#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
struct jz
{
int a[3][3];
};
jz mul(jz x,jz y)
{
jz res;
res.a[1][1]=((long long)x.a[1][1]*y.a[1][1]%mod+(long long)x.a[1][2]*y.a[2][1]%mod)%mod;
res.a[1][2]=((long long)x.a[1][1]*y.a[1][2]%mod+(long long)x.a[1][2]*y.a[2][2]%mod)%mod;
res.a[2][1]=((long long)x.a[2][1]*y.a[1][1]%mod+(long long)x.a[2][2]*y.a[2][1]%mod)%mod;
res.a[2][2]=((long long)x.a[2][1]*y.a[1][2]%mod+(long long)x.a[2][2]*y.a[2][2]%mod)%mod;
return res;
}
jz base;
jz qmi(jz x,long long n)
{
jz res;
res.a[1][1]=res.a[2][2]=1;
res.a[1][2]=res.a[2][1]=0;
while(n)
{
if(n&1) res=mul(res,x);
x=mul(x,x);
n>>=1;
}
return res;
}
int main()
{
base.a[1][1]=0;
base.a[1][2]=base.a[2][1]=base.a[2][2]=1;
long long n;
scanf("%lld",&n);
jz ans=qmi(base,n-1);
// cout<<ans.a[1][1]<<" "<<ans.a[1][2]<<" "<<ans.a[2][1]<<" "<<ans.a[2][2]<<endl;
jz m;
m.a[1][1]=m.a[1][2]=1;
m.a[2][1]=m.a[2][2]=0;
ans = mul(m,ans);
//cout<<ans.a[1][1]<<" "<<ans.a[1][2]<<" "<<ans.a[2][1]<<" "<<ans.a[2][2]<<endl;
int res=(long long)ans.a[1][1]*ans.a[1][2]%mod;
cout<<res;
}
问题 K: 数轴世界郊游（问题 K: 数轴世界郊游 - BUCTOJ）
思路：这题是贪心题，哎，怎么说呢，我最开始没注意到一个点只能放一个居民，于是算出了查询区间中最多有多少个既定区间（虽然与本题无关，但是还是稍微写一下思路吧，万一下次遇到呢，大致思路就是按照左端从小到大排，左端点相同的，按照右端点从小到大排，对于查询区间[l,r]，找出r左边的左端点数量和l左边的右端点数量，然后相减就解决了）
回到这个题，每个点只能放一个居民，我们把居民喜爱的区间作为它的属性，对于查询区间，只有居民的喜爱区间在这里面才能被计入，但是同一个点的位置可能有很多个居民喜爱，那么我们该把这个点分给哪个居民呢？
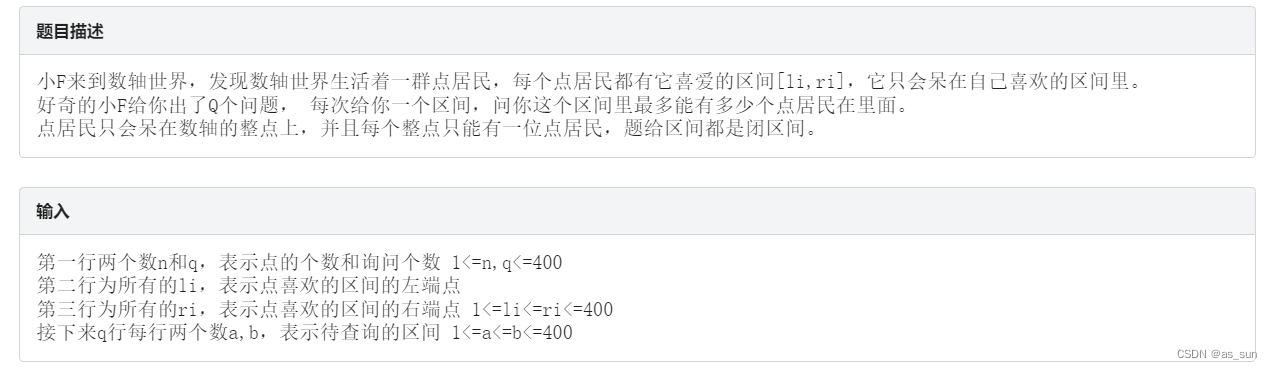
如图，红色区间是查询区间，有两个居民的喜爱区间都有一部分在里面，而且他们第一个点是重叠的，那么这个点分给谁呢，显然是分给右端点小的那个居民比较合适，因为右端点大的还可以放后面。所以局部最优策略就出来了，尽量将点分给右端点小的居民。贪心的核心就是局部最优，同时不被其他的影响，那么我们就来验证下这个策略。将所有的居民区间按照右端点从小到大排序，如果右端点相同，那么按照左端点从小到大排，因为左端大的也是可以被放进后面。然后对于每个查询，我们遍历居民区间，如果在查询区间内部，那么就遍历查询区间找一个点分给它，答案加1，最后输出答案。
#include<bits/stdc++.h>
using namespace std;
int l[1000],r[1000];
struct node
{
int l,r;
}c[1000];
bool cmp(node a,node b)
{
if(a.r!=b.r) return a.r<b.r;
else return a.l>b.l;
}
int st[500];
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) scanf("%d",&c[i].l);
for(int i=1;i<=n;i++) scanf("%d",&c[i].r);
sort(c+1,c+1+n,cmp);
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
int ans=0;
memset(st,0,sizeof st);
for(int i=1;i<=n;i++)
{
if(c[i].r<a||c[i].l>b) continue;
for(int j=a;j<=b;j++)
{
if(st[j]||j<c[i].l||j>c[i].r) continue;
else
{
ans++;
st[j]=1;
break;
}
}
}
cout<<ans<<endl;
}
}ps:这里很重要的一个地方就是，一个点处可能有好几个居民，所以放哪个涉及到选择，选择策略这种要么贪心要么动态规划。这里显然动态规划讨论不方便，贪心就可解决。
问题 L: 超级斐波那契（问题 L: 超级斐波那契 - BUCTOJ）
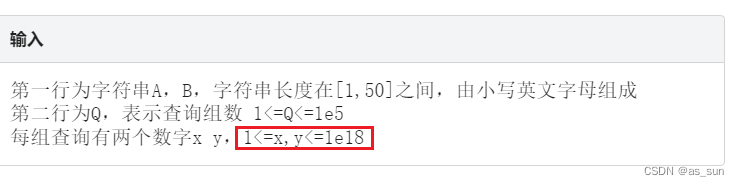
这题看似很麻烦，但有个很关键的点:y<=1e18,所以大于1e18的位就不用看了。
由于斐波那契数列的增长很快，我打表看了下，f[1]=f[2]=1的情况下，f[88]>1e18，所以我们可以在很少的处理下就得到1e18。
这道题肯定是将查询转移到前面给定的A和B中，那么关键就是如何转移：
F[x]=F[x-1]+F[x-2]
所以,如果查询x的第y位，有两种情况：
y<=f[x-1]，那么就是查询x-1的第y位
如果y>f[x-1],那么就是查询x-2的第y-f[x-1]位，
那么递归将待查询的位数转移到第一项或者第二项中即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
int f[1000];
char a[100],b[100];
void dfs(int x,int y)
{
if(x==1)
{
cout<<a[y]<<endl;
return ;
}
if(x==2)
{
cout<<b[y]<<endl;
return;
}
if(y<=f[x-1]) dfs(x-1,y);
else dfs(x-2,y-f[x-1]);
}
signed main()
{
scanf("%s%s",a+1,b+1);
f[1]=strlen(a+1);
f[2]=strlen(b+1);
int idx;
for(int i=3;i<=100;i++)
{
f[i]=f[i-1]+f[i-2];
if(f[i]>1e18)
{
idx=i;
break;
}
}
int q;
scanf("%lld",&q);
while(q--)
{
int x,y;
scanf("%lld%lld",&x,&y);
if(x>idx) dfs(idx,y);
else dfs(x,y);
}
}
问题 M: 数字显示屏仿真（问题 M: 数字显示屏仿真 - BUCTOJ）
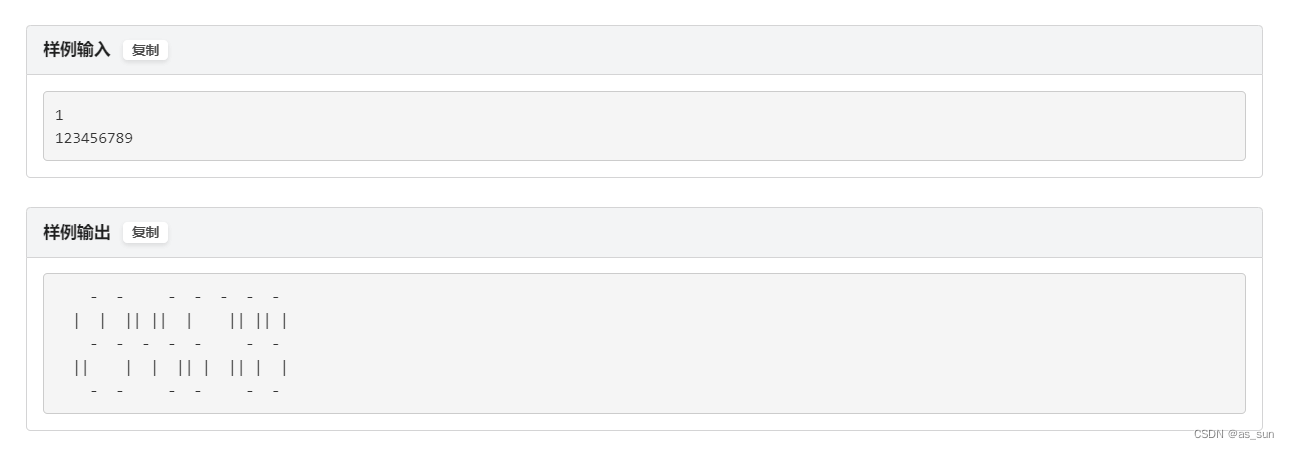
思路：这里我专门把样例贴上，来找规律，很显然结果是由5行构成的：
1，3，5行对于每一个数只有一下两种情况：0-0,000(0表示空格)
2，4行有四种情况：101，100，001，000（0表示空格）
那么我们只要对于每个数，处理出来它每一行的状态，然后根据状态一行一行输出即可。
特别注意！！！要记得清空数组，而且给出的那组样例是不在测试数据中的（我可不说是谁忘记清空wa了两三次）
#include<bits/stdc++.h>
using namespace std;
string v[6];
int main()
{
int k;
scanf("%d",&k);
while(k--)
{
string s;
cin>>s;
int l=s.size();
for(int i=0;i<l;i++)
{
if(s[i]=='0')
{
v[1].push_back('1');
v[2].push_back('1');
v[3].push_back('0');
v[4].push_back('1');
v[5].push_back('1');
}
else if(s[i]=='1')
{
v[1].push_back('0');
v[2].push_back('3');
v[3].push_back('0');
v[4].push_back('3');
v[5].push_back('0');
}
else if(s[i]=='2')
{
v[1].push_back('1');
v[2].push_back('3');
v[3].push_back('1');
v[4].push_back('2');
v[5].push_back('1');
}
else if(s[i]=='3')
{
v[1].push_back('1');
v[2].push_back('3');
v[3].push_back('1');
v[4].push_back('3');
v[5].push_back('1');
}
else if(s[i]=='4')
{
v[1].push_back('0');
v[2].push_back('1');
v[3].push_back('1');
v[4].push_back('3');
v[5].push_back('0');
}
else if(s[i]=='5')
{
v[1].push_back('1');
v[2].push_back('2');
v[3].push_back('1');
v[4].push_back('3');
v[5].push_back('1');
}
else if(s[i]=='6')
{
v[1].push_back('1');
v[2].push_back('2');
v[3].push_back('1');
v[4].push_back('1');
v[5].push_back('1');
}
else if(s[i]=='7')
{
v[1].push_back('1');
v[2].push_back('3');
v[3].push_back('0');
v[4].push_back('3');
v[5].push_back('0');
}
else if(s[i]=='8')
{
v[1].push_back('1');
v[2].push_back('1');
v[3].push_back('1');
v[4].push_back('1');
v[5].push_back('1');
}
else
{
v[1].push_back('1');
v[2].push_back('1');
v[3].push_back('1');
v[4].push_back('3');
v[5].push_back('1');
}
}
for(int i=1;i<=5;i++)
{
if(i%2)
{
for(int j=0;j<l;j++)
{
if(v[i][j]=='1') printf(" - ");
else printf(" ");
}
}
else
{
for(int j=0;j<l;j++)
{
if(v[i][j]=='1') printf("| |");
else if(v[i][j]=='2') printf("| ");
else if(v[i][j]=='3')printf(" |");
else printf(" ");
}
}
printf("\n");
}
for(int i=1;i<=5;i++) v[i].clear();
}
}
