目录

1  53. 最大子数组和

2  56. 合并区间

3  189. 轮转数组

4  238. 除自身以外数组的乘积

5  41. 缺失的第一个正数

---

菜鸟做题第二周，语言是 C++

1  53. 最大子数组和

题眼：“子数组是数组中的一个连续部分。”

遍历数组，问每一个元素 “你愿不愿意和前面那伙人一起干啊”，如果该元素不愿意，那么就让它另起炉灶。那该元素的评判标准是什么呢？当然是评估搭伙和单干哪个更好啦。具体来说，就是评估自己本身的值和求和后的值哪个大。如下图所示：

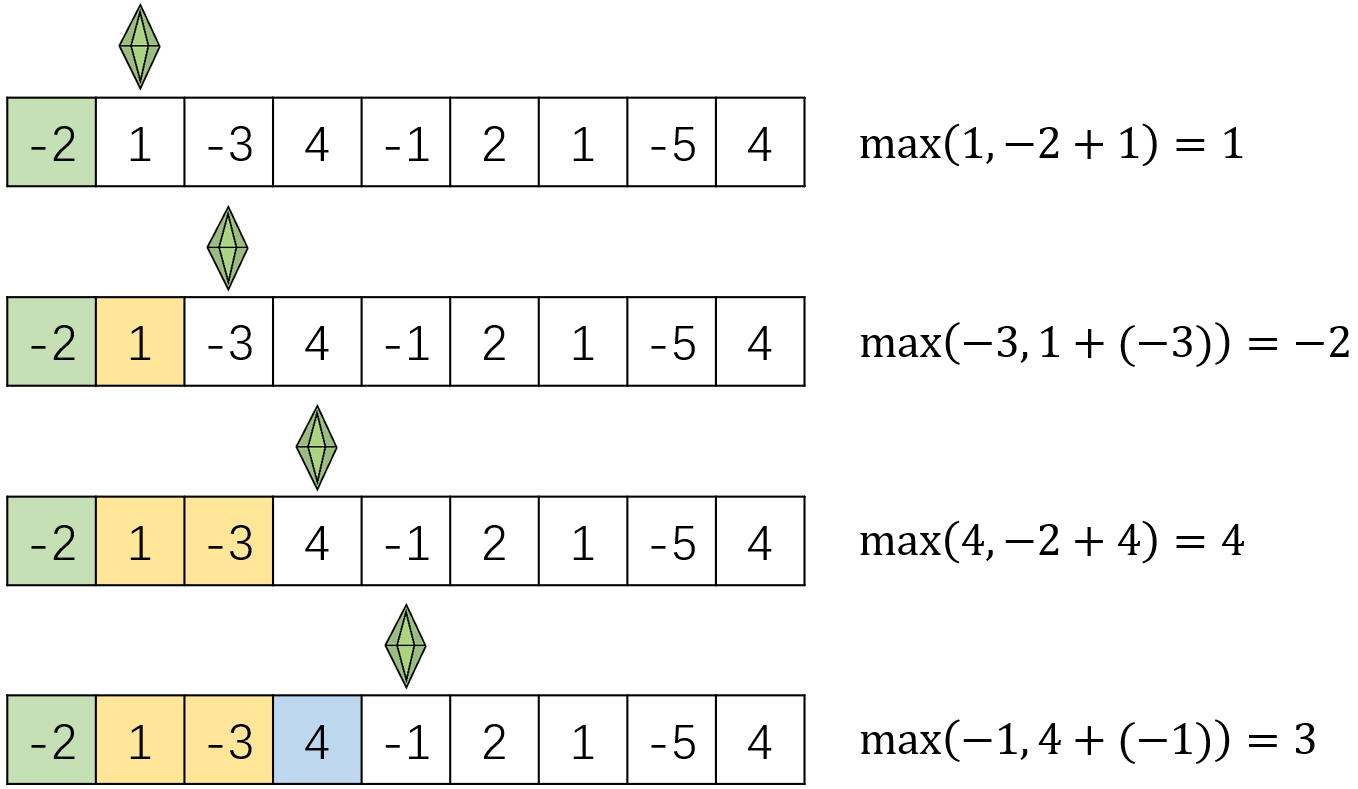
比如：对于元素 1，它自己的值是 1，加上 -2 后是 -1，那它当然更愿意自立门户啦。对于元素 4，它自己的值是 4，加上（1 和 -3）后是 2，那它当然也更愿意自立门户。

解题的关键就在于子数组是连续的，每个元素都只能选择要不要和自己前面的那伙人一起。

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
       int pre = 0, maxAns = nums[0];
        for (const auto &x: nums) {
            pre = max(pre + x, x);
            maxAns = max(maxAns, pre);
        }
        return maxAns;
    }
};

一开始我想学以致用，把子数组的和转换为前缀和的差，但实际上不太行。具体来说，就是我想找最大前缀和来减最小前缀和，认为它们之差对应的子数组的和就是最大的。但问题在于，最大前缀和可能比最小前缀和短，对应于它们之差的子数组是不存在的。

2  56. 合并区间

解题思路：

1. 首先按区间的左端大小为它们排序
2. 定义左指针 left 和右指针 right
3. 固定 left，让 right 从左往右寻找可以合并的区间
4. 当找不到时，存入合并后的区间并移动 left

思路说明图：

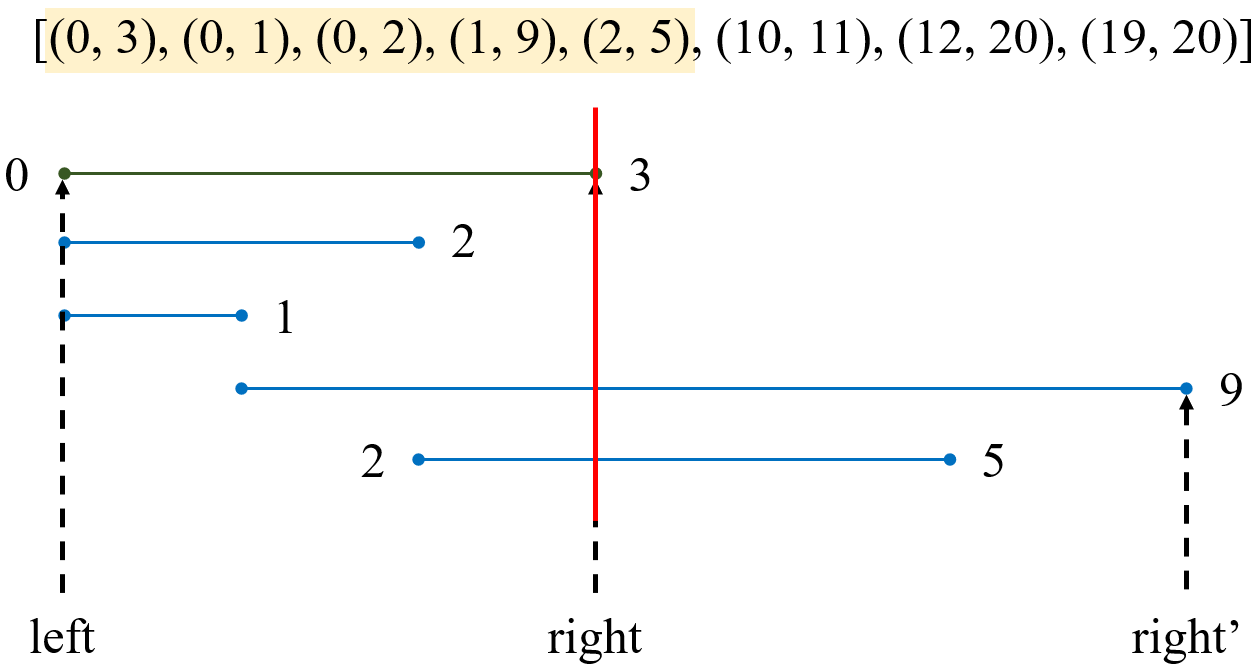
我们以 (0, 3) 开始找能够与它合并的区间。合并的条件是什么呢？答案是：只要其他区间的左值小于 (0, 3) 的右值即可。这些区间又分为两类：一类是被 (0, 3) 包含的，比如 (0, 1)；另一类是没有被包含的，比如 (2, 5)。对于被包含的区间，我们不用理它；对于没有被包含的区间，我们比较它的右值和当前的 right 谁大，取较大值来更新 right 。

由于是扫描到不能合并的区间为止，因此下一轮我们直接从那个区间，即 (10, 11) 开始寻找，而不是从 (0, 3) 的下一个，即 (0, 1) 开始寻找。

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        int n = intervals.size();
        sort(intervals.begin(), intervals.end());
        vector<vector<int>> ans;

        int i = 0, left, right;
        while (i < n) {
            left = intervals[i][0];
            right = intervals[i][1];
            while (i < n && intervals[i][0] <= right) {
                right = max(right, intervals[i][1]);
                ++i;
            }
            ans.push_back({left, right});
        }

        return ans;
    }
};

3  189. 轮转数组

由于没有额外的要求，因此搞个临时数组装好了再替换回去即可：

class Solution {
public:
    void rotate(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> rotate(n);

        for (int i = 0; i < n; ++i) {
            rotate[(i + k) % n] = nums[i];
        }
        nums = rotate;
    }
};

4  238. 除自身以外数组的乘积

解题思路：

1. 从左往右遍历，计算并存储所有的前缀乘积
2. 从右往左遍历，计算并存储所有的后缀乘积
3. 最后对应相乘，即为结果

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> left(n), right(n), ans(n);

        // 从左往右
        int pre = 1;
        left[0] = pre;
        for (int i = 0; i < n - 1; ++i) {
            pre *= nums[i];
            left[i + 1] = pre;
        }

        // 从右往左
        int post = 1;
        right[n - 1] = post;
        for (int i = n - 1; i >= 1; --i) {
            post *= nums[i];
            right[i - 1] = post;
        }

        // 对应相乘
        for (int i = 0; i < n; ++i) {
            ans[i] = left[i] * right[i];
        }
        return ans;
    }
};

5  41. 缺失的第一个正数

解题思路：

1. 把 nums 中的所有数存入集合 set 中
2. 从正整数 1 开始在 set 中查找
3. 找不到的即为缺失的第一个正整数

我觉得我这个逻辑比较清晰，就是执行时间比较长。

class Solution {
public:
    int firstMissingPositive(vector<int>& nums) {
        unordered_set<int> set;
        for (auto &n:nums) {
            set.insert(n);
        }
        int min = 1;
        while (set.find(min) != set.end()) {
            ++min;
        }
        return min;
    }
};