小蓝有一个保险箱，保险箱上共有 n 位数字。

小蓝可以任意调整保险箱上的每个数字，每一次操作可以将其中一位增加 1 或减少 1。

当某位原本为 9 或 0 时可能会向前（左边）进位/退位，当最高位（左边第一位）上的数字变化时向前的进位或退位忽略。

例如:

00000 的第 5 位减 1 变为 99999；

99999 的第 5 位减 1 变为 99998；

00000的第 4 位减 1 变为 99990；

97993 的第 4 位加 1 变为 98003；

99909 的第 3 位加 1 变为 00009。

保险箱上一开始有一个数字 x，小蓝希望把它变成 y，这样才能打开它，问小蓝最少需要操作的次数。

输入格式

输入的第一行包含一个整数 n。

第二行包含一个 n 位整数 x。

第三行包含一个 n 位整数 y。

输出格式

输出一行包含一个整数表示答案。

数据范围

对于 30% 的评测用例，1≤n≤300；
对于 60% 的评测用例，1≤n≤3000；
对于所有评测用例，1≤n≤10^5，x,y中仅包含数字 0 至 9，可能有前导零。

输入样例：

5
12349
54321

输出样例：

11

 思路：

题目要求通过操作将一个 n 位的数字 x 调整为另一个 n 位的数字 y，且调整的操作次数最少。每一次操作可以将数字的某一位增加 1 或减少 1，同时需要考虑进位和退位的情况。

我们可以使用动态规划来解决这个问题。定义一个二维数组 dp，其中 dp[i][j] 表示将 x 的前 i 位调整为 y 的前 i 位时，最少需要的操作次数，且最高位为 j。我们可以从左到右逐位计算 dp 数组。

以下是详细的步骤：

1. 初始化一个二维数组 dp，大小为 (n+1) * 10。其中 dp[i][j] 表示将 x 的前 i 位调整为 y 的前 i 位时，最少需要的操作次数，且最高位为 j。初始化为一个较大的值，比如 INF。

2. 设置初始状态，即 dp[0][j]，表示将空字符串调整为 y 的前 0 位时，最少需要的操作次数。这里只有一种情况，即空字符串调整为空字符串，操作次数为 0。因此 dp[0][j] = 0。

3. 逐位计算 dp 数组。对于每一位 i 和可能的值 j，计算 dp[i][j]。具体计算方式如下：

   • 对于 j = 0 到 9，表示当前位的可能取值。
   • 对于当前位 i，计算从 x[i] 调整到 y[i] 的最小操作次数。假设 x[i] 的值为 xi，y[i] 的值为 yi。
   • 对于每个可能的进位 k，计算从 xi 调整到 yi 的最小操作次数，即 abs(xi + k - yi)。
   • 更新 dp[i][j] 为上述所有情况的最小值。

4. 最终答案为 dp[n][y[0]]，表示将 x 的所有位数调整为 y 的所有位数时，最少需要的操作次数，且最高位为 y[0]。

 

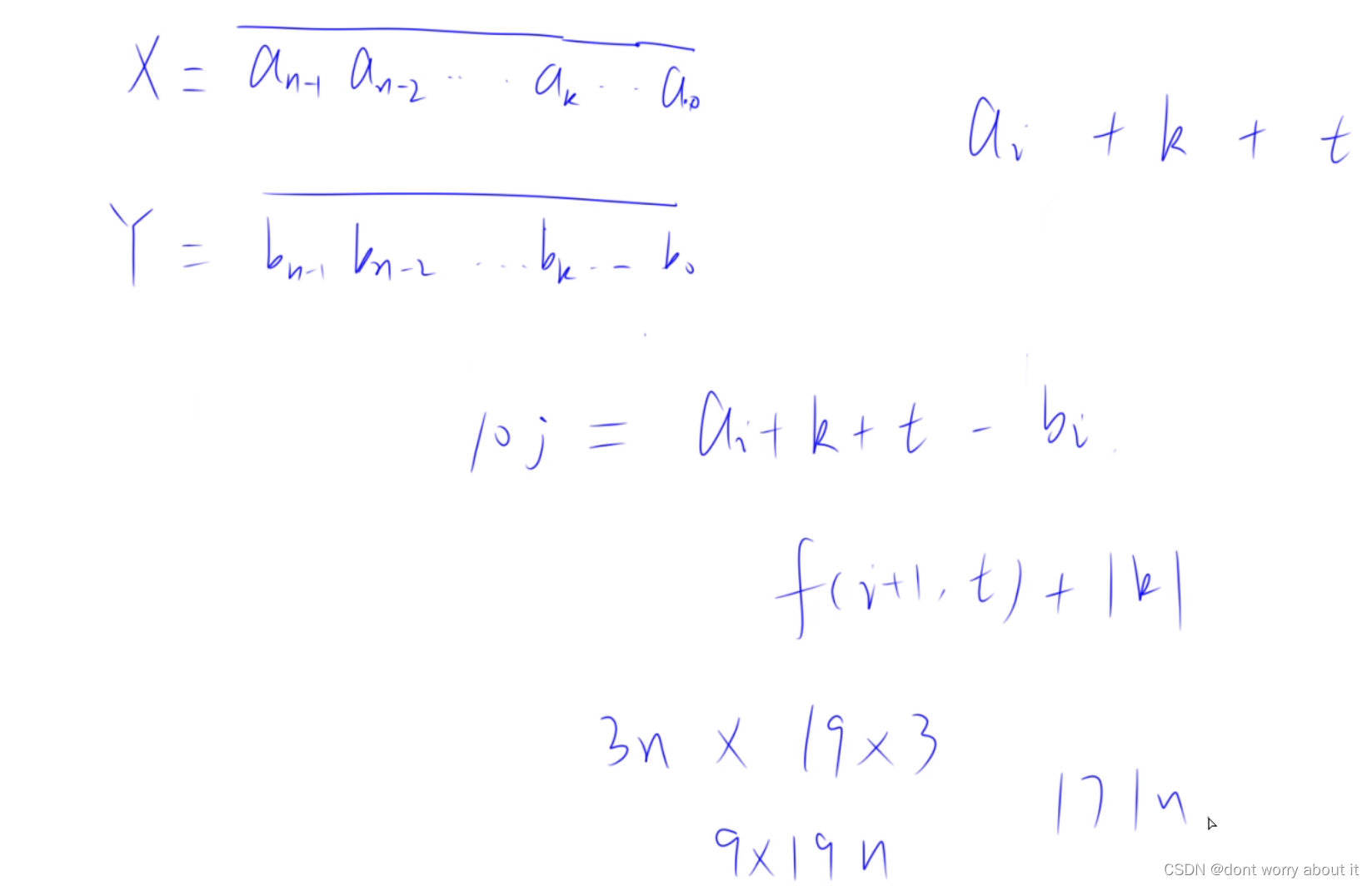
完整代码：

#include <iostream>
using namespace std;
#include <cstring>
#include <algorithm>
const int N=100010;
int n;
char a[N],b[N];
int dp[N][3];

int main(){
    cin>>n>>a>>b;
    memset(&dp,0x3f,sizeof(dp));
    dp[n][1]=0;
    for(int i=n-1;i>=0;i--)
        for(int j=0;j<3;j++)
            for(int k=-9;k<=9;k++)
                for(int t=0;t<3;t++)
                    if(a[i]+k+t-1-b[i]==(j-1)*10)
                    dp[i][j]=min(dp[i][j],dp[i+1][t]+abs(k));
    cout<<min({dp[0][0],dp[0][1],dp[0][2]})<<endl;
}