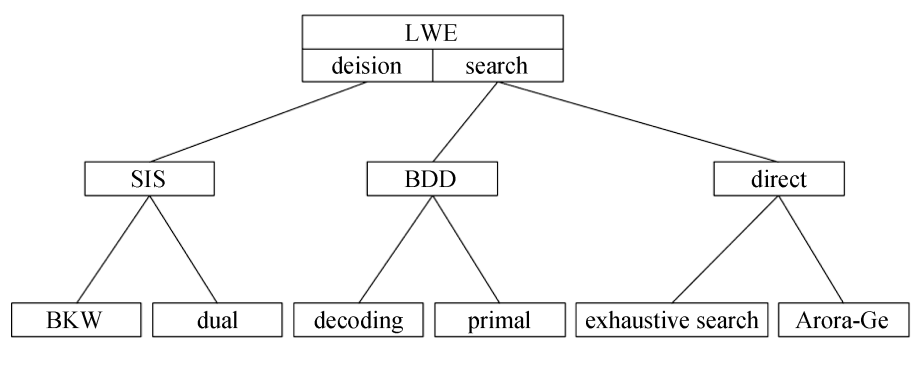
目录
一. 介绍
二. LWE密码方案简单介绍
三. LWE经典归约
四. LWE性质
五. LWE的鲁棒性
一. 介绍
在2005年,Regev基于LWE问题提出了一个新的公钥密码方案。该方案可实现语义安全(semantic security),其中误差率(error rate)为:
其安全性可利用量子算法归约到近似GapSVP和SIVP问题,其中近似因子取:
该方案借鉴了两个工作,一个是1997年Ajtai-Dwork的工作,一个是2003年Regev的工作。但相比之下有两大优点比较突出。
优点1:一般性(generality)
该方案依赖的最坏(worst case)情况是近似GapSVP和近似SIVP问题。在网路安全领域,还有一个问题叫近似unique-SVP问题,有时也简称为uSVP问题。该问题的结构性太强了,不太适合进行归约证明困难性。
优点2:效率更高
有关密码方案的效率,我们关注很多方面,比如公钥尺寸,以前的方案公钥尺寸是,该方案是
。
每次加密一个明文比特,私钥和密文的尺寸是一样的为:
相比以前的方案是:
如果将该方案推广到多用户,情况则变得很有意思。2005年,Ajtai指出可以利用密码方案来实现公共随机性共享,但很遗憾还不能证明其符合最坏情况的安全性。如果此过程能实现的话,那么所有用户共享的随机比特串可设定为:
此时每个用户的公钥尺寸为:
二. LWE密码方案简单介绍
实际上Regev的基于LWE的密码方案和安全性证明都和Ajtai-Dwork的工作很类似,所以此处就简单解释下。
方案的私钥为s,格式如下:
很明显可以说明私钥尺寸为
公钥则是随机选取一些LWE样本,当然这些样本对应的秘密s是一样的,如下:
假定样本个数近似n个,那么很容易计算公钥尺寸为:
加密时,选择加密一个比特。从刚才的公钥LWE样本中选择一部分子集,然后相加,最后把消息比特隐藏于结果的最后一位,很容易计算密文的尺寸为:
那么怎么解密呢?
密文要么很接近垂直于(-s,1)的子空间,要么很远。拥有私钥的人,则可以区分,也就可以解密出比特0或者比特1
当然密码学中,要想说明语义安全是需要设定严格的安全性证明试验。在敌手看来,根据LWE问题的困难性,是无法区分真随机分布和LWE分布的。

而且在这种设计的密钥下加密,是loosy的,也就是密文和明文信息比特是统计独立的,那么敌手区分加密0和加密1的优势则是可忽略的。
详细的密码方案在“格密码专栏”中,后续会不断更新。
在2005年,Regev提出LWE之后,有关其额外的困难性定理就不断涌现出来,比如基于经典归约的,基于leaky密钥的,更小的误差,更小的模等等,接下来本文章将解释几个比较重要的提高和扩展。
三. LWE经典归约
Regev利用量子算法实现了最坏情况归约,在2009年Peikert去量子化(dequantized),利用经典算法也实现了归约。其格公钥密码也依赖于一般格(genaral lattice),该格的结构性没有那么强(相比unique shortest vectors)。设定LWE问题的错误率为,其困难性可以归约到最坏情况的近似GapSVP问题,其中近似因子为:
量子归约到GapSVP和SIVP问题上,但目前经典归约只能到GapSVP问题。
经典归约要求模数得指数大小,也就是在LWE问题中q的范围满足:
量子归约只需要多项式尺寸大小的模数,也就是:
当然其实经典归约也可以到q=poly(n)的尺寸,但是这时对应的不是标准的GapSVP问题类型。
为啥我们对模数q的大小这么关注呢?

大的模数意味着在表示LWE样本时,需要更多的比特,导致密钥的尺寸变大,密码系统的效率则降低。
虽然经典归约还有许多限制,但是并不妨碍利用LWE问题来构建有效的密码学方案。
四. LWE性质
在2009年,Pei和Lyubashevsky-Micciancio分别在两篇论文中证明了,利用经典归约已经近似因子等于poly(n)时,以下几个问题是等效的:
GapSVP,uSVP,BDD
这也就意味着,虽然说Ajtai-Dwork的密码系统最开始是依赖uSVP问题的,但其实也可以依赖于GapSVP问题。
在2013年,Brakerski等人认为需要平衡LWE问题的维度与模数。他们认为,在固定错误率的前提下,LWE问题的困难性可以用nlogq来衡量,也就是跟n和q都有关系。举个例子来解释为什么这个结论很有用。

比如说,Peikert认为LWE可归约到n维格上的GapSVP问题,此时模数q满足:
如果我们将维度提升到,那么模数就只需要q=poly(n)即可。
此方案的证明过程使用到了全同态(fully homomorphic encryption)中的密钥切换(key switching)和模归约(modulus reduction)。当然只是借鉴这些技术,实际上会更加复杂,因为需要产生对应的LWE样本,而不是单纯的拥有小误差的样本。
五. LWE的鲁棒性
robustness,通常翻译成鲁棒性。
已有的研究表明,及时敌手学习到了关于秘密和错误的一些额外信息,LWE问题依旧是困难的。