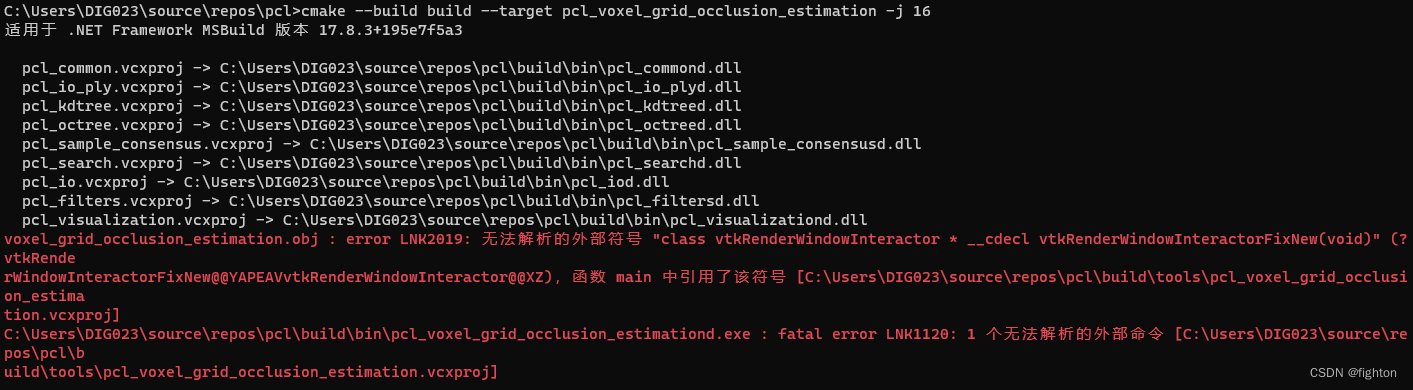
问题描述

什么是拓扑序列

• 若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x 在 A 中都出现在 y 之前，则称 A 是该图的一个拓扑序列。
• 图中不能有环
• 图中至少存在一个点的入度为0

如何求拓扑序列？

• 计算出每个节点的入度
• 遍历每个节点，将入度为0的节点存入队列中
• 每次从队头中取出一个元素，遍历当前元素指向的下一个节点，将下一个节点的入度减1，如果入度为0，那么将下一个节点插入队尾中
• 直到队列中没有元素
• 如果有n个节点插入过队列中，那么这个图存在拓扑序列，入队顺序就是拓扑序列

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 10;

int n, m;
int h[N], ne[N], e[N], idx;
int in[N];	// 存储当前节点的入度
int q[N];	// 数组模拟队列

void add(int a, int b)
{
	e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void bfs()
{
	int hh = 0, tt = -1;	// 队列头、尾指针
	for(int i = 1; i <= n; i++)	// 将入度为0的节点插入队尾中
	{
		if(in[i] == 0) q[++tt] = i;
	}
	while(hh <= tt)
	{
		int t = q[hh++];	// 弹出队头元素
		for(int i = h[t]; i != -1; i = ne[i])	// 队头元素指向的下一个节点
		{
			int j = e[i];
			in[j]--;	// 入度减1
			if(in[j] == 0) q[++tt] = j;	// 入度为0，插入队尾中
		}
	}
	if(tt == n - 1)	// 如果队列中插入了n个节点（所有节点都入过队列），那么这个图有拓扑序列
	{
		for(int i = 0; i <= tt; i++) cout << q[i] << " ";
	}
	else cout << -1 << endl;
}

int main()
{
	cin >> n >> m;
	memset(h, -1, sizeof h);
	for(int i = 0; i < m; i++)
	{
		int a, b;
		cin >> a >> b;
		in[b]++;	// 将节点b入度+1
		add(a, b);
	}
	
	bfs();
	
	return 0;
}