KDE图是什么?
核密度估计(Kernel Density Estimate,KDE)是一种非参数统计方法,用于估计未知随机变量的概率分布。它通过在每个数据点附近放置一个核函数,并将这些核函数加总起来,得到对概率分布的估计。
KDE的主要思想是通过在每个数据点附近放置一个核函数来估计概率分布。核函数可以是各种形式,常用的有高斯核、均匀核等。核函数在数据点附近产生一个非负的函数值,表示该点附近的概率密度。然后,将所有核函数的值加总起来,得到整个数据集的概率密度函数。
KDE图可以理解为是对直方图的加窗平滑。KDE图解决了一个基本的数据平滑问题,即根据有限的数据样本对总体进行推断。通过KDE分布图,可以查看并对训练数据集和测试数据集中特征变量的分布情况。
KDE图定义
设 (x1,x2,...,xn) 是从某个单变量分布中抽取的独立同分布样本,在任何给定点 x 具有未知密度 f 。我们有兴趣估计这个函数 f 的形状。它的核密度估计量是:

其中 K 是内核——一个非负函数——h > 0 是一个称为带宽的平滑参数。下标为 h 的内核称为缩放内核,定义为 Kh(x) = 1/h K(x/h)。直觉上,人们希望选择数据允许的尽可能小的 h;然而,估计量的偏差与其方差之间总是存在权衡。
通常使用一系列核函数:uniform、triangular、biweight、triweight、Epanechnikov、normal 等。Epanechnikov 内核在均方误差意义上是最优的,尽管前面列出的内核的效率损失很小。 由于其方便的数学性质,常使用正态核,即 K(x) = ϕ(x),其中 ϕ 是标准正态密度函数。核密度估计的构建在密度估计之外的领域找到了解释。 例如,在热力学中,这相当于将热核(热方程的基本解)放置在每个数据点位置 xi 时产生的热量。类似的方法用于在点云上构建离散拉普拉斯算子以进行流形学习(例如扩散图)。
例子
核密度估计与直方图密切相关,但可以通过使用合适的核赋予平滑度或连续性等属性。下图基于这 6 个数据点说明了这种关系:
| 样品 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 值 | -2.1 | -1.3 | -0.4 | 1.9 | 5.1 | 6.2 |
对于直方图,首先,水平轴被划分为覆盖数据范围的子区间或区间:在这种情况下,每个区间有 6 个宽度为 2 的区间。每当一个数据点落在该区间内时,一个高度为 1 的区间/12 放在那里。如果不止一个数据点落在同一个箱子里,这些箱子就会堆叠在一起。对于核密度估计,将方差为 2.25 的正态核(由红色虚线表示)放置在每个数据点 xi 上。对内核求和以进行内核密度估计(蓝色实线)。核密度估计的平滑性(与直方图的离散性相比)说明了核密度估计如何更快地收敛到连续随机变量的真实基础密度。
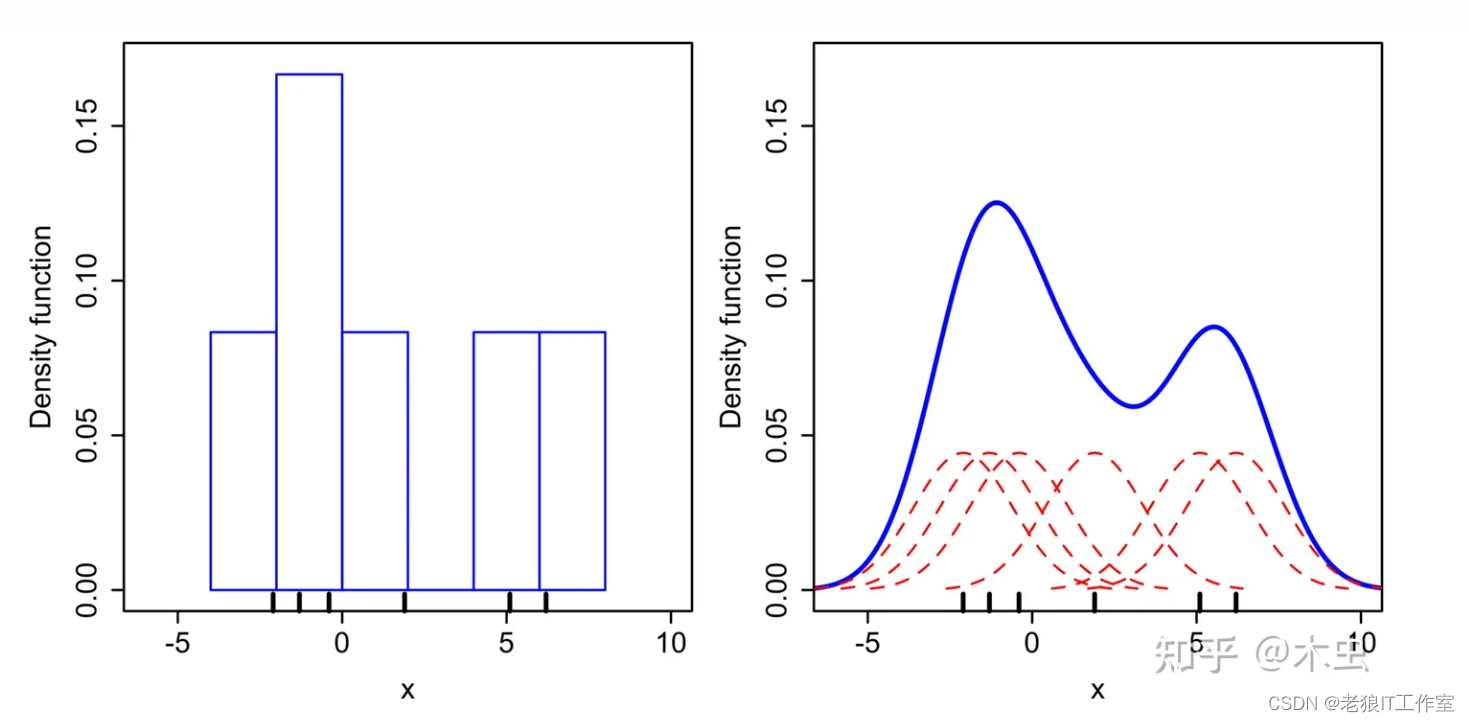
使用相同数据构建的直方图(左)和核密度估计(右)的比较。 六个单独的内核是红色虚线,内核密度估计蓝色曲线。 数据点是横轴上的地毯图。
如上图的右图所示,我理解的红色曲线就是基函数,类似于傅里叶函数的基函数叠加形成上面的蓝色曲线。
KDE图使用场景
KDE可以用于多种场景,其中一些案例包括:
-
数据可视化:KDE可以用来绘制密度图,可以清晰地展示数据分布的形态。例如,在金融领域,可以使用KDE绘制股票收益率的密度图,以帮助理解收益率的分布情况。
-
数据挖掘:KDE可以用于异常检测。通过估计数据的概率密度分布,可以确定哪些数据点的概率较低,从而识别出异常点。例如,在网络安全领域,可以使用KDE来检测网络流量中的异常活动。
-
信号处理:KDE可以用于信号处理中的噪声估计。通过估计信号的概率密度分布,可以确定噪声的分布情况,进而进行噪声滤波等操作。
KDE图使用案例
在这个例子中,我们导入了tips数据集,并使用sns.kdeplot()函数绘制了total_bill变量的KDE图和直方图。可以使用title()和xlabel()函数设置图表标题和轴标签。最后,使用plt.show()函数显示图表。
import matplotlib.pyplot as plt
import seaborn as sns
# 导入数据集
tips = sns.load_dataset('tips')
tips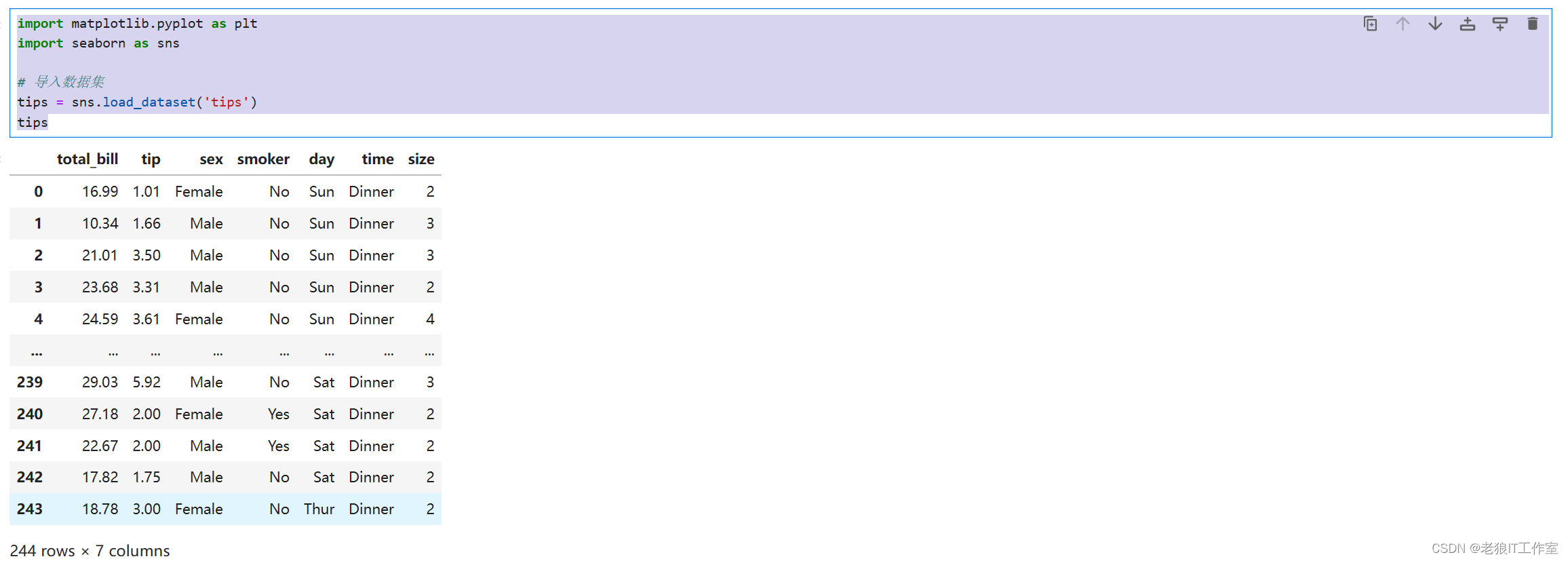
# 绘制KDE图
sns.kdeplot(data=tips, x='total_bill')
# 设置图表标题和轴标签
plt.title('KDE Plot of Total Bill')
plt.xlabel('Total Bill')
# 显示图表
plt.show()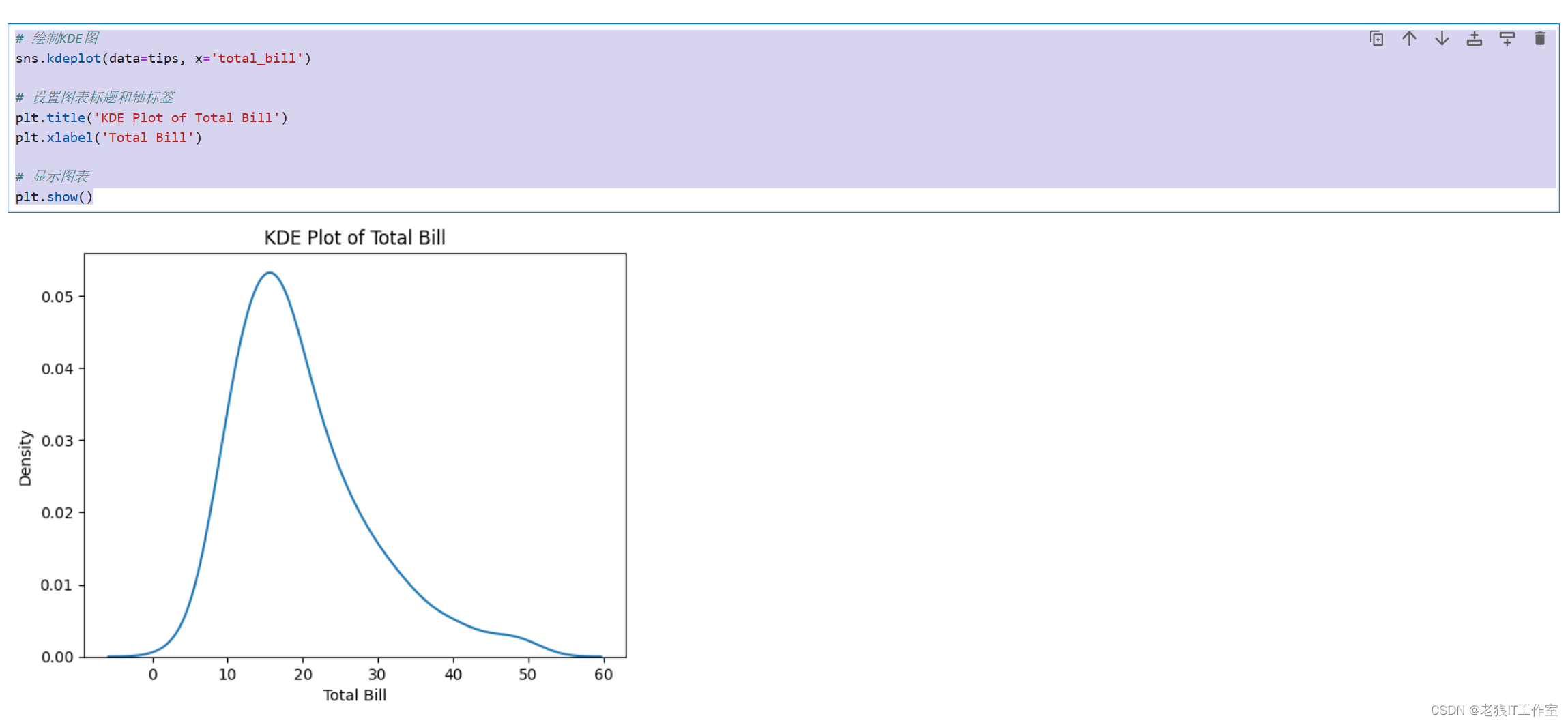
# 绘制直方图
sns.histplot(data=tips, x='total_bill')
# 设置图表标题和轴标签
plt.title('Hist Plot of Total Bill')
plt.xlabel('Total Bill')
# 显示图表
plt.show()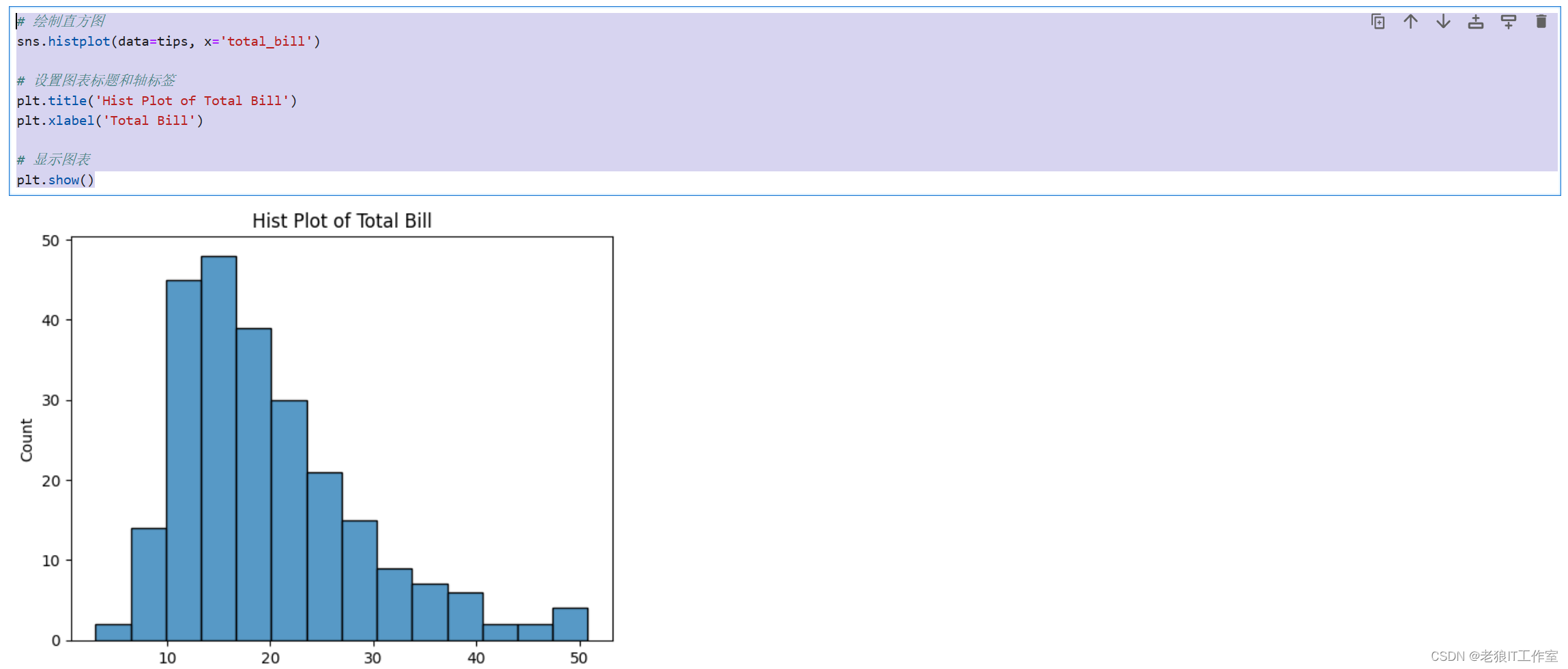
结论
总之,KDE是一种非参数统计方法,可以用于估计未知随机变量的概率分布。它在数据可视化、数据挖掘和信号处理等领域都有广泛的应用。
参考资料
KDE: Kernel density estimation 核密度估计