哈夫曼树(Huffman)

news2024/9/29 3:22:32

哈夫曼树

Huffman 编码问题

问题引入

什么是编码？

简单说就是建立【字符】到【数字】的对应关系，如下面大家熟知的 ASC II 编码表，例如，可以查表得知字符【a】对应的数字是十六进制数【0x61】

\	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
0000	00	01	02	03	04	05	06	07	08	09	0a	0b	0c	0d	0e	0f
0010	10	11	12	13	14	15	16	17	18	19	1a	1b	1c	1d	1e	1f
0020	20	!	"	#	$	%	&	’	(	)	*	+	,	-	.	/
0030	0	1	2	3	4	5	6	7	8	9	:	;	<	=	>	?
0040	@	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O
0050	P	Q	R	S	T	U	V	W	X	Y	Z	[	\	]	^	_
0060	`	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o
0070	p	q	r	s	t	u	v	w	x	y	z	{	\|	}	~	7f

注：一些直接以十六进制数字标识的是那些不可打印字符

传输时的编码

java 中每个 char 对应的数字会占用固定长度 2 个字节
如果在传输中仍采用上述规则，传递 abbccccccc 这 10 个字符
- 实际的字节为 0061006200620063006300630063006300630063（16进制表示）
- 总共 20 个字节，不经济

现在希望找到一种最节省字节的传输方式，怎么办？

假设传输的字符中只包含 a，b，c 这 3 个字符，有同学重新设计一张二进制编码表，见下图

0 表示 a
1 表示 b
10 表示 c

现在还是传递 abbccccccc 这 10 个字符

实际的字节为 01110101010101010 （二进制表示）
总共需要 17 bits，也就是 2 个字节多一点，行不行？

不行，因为解码会出现问题，因为 10 会被错误的解码成 ba，而不是 c

解码后结果为 abbbababababababa，是错误的

怎么解决？必须保证编码后的二进制数字，要能区分它们的前缀（prefix-free）

用满二叉树结构编码，可以确保前缀不重复

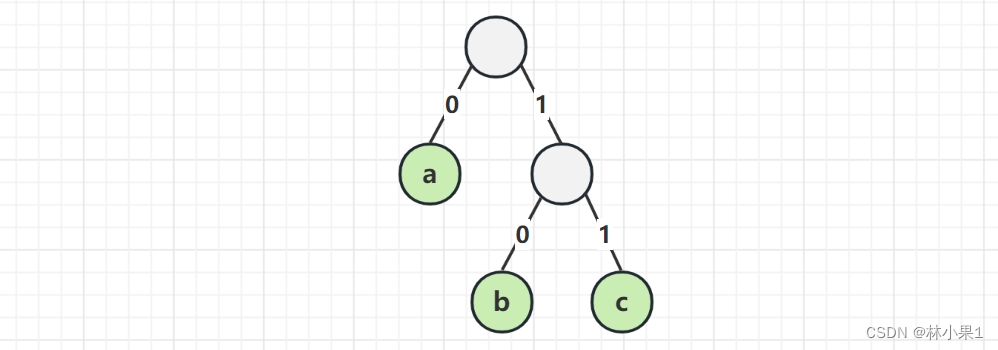
请添加图片描述

向左走 0，向右走 1
走到叶子字符，累计起来的 0 和 1 就是该字符的二进制编码

再来试一遍

a 的编码 0
b 的编码 10
c 的编码 11

现在还是传递 abbccccccc 这 10 个字符

实际的字节为 0101011111111111111（二进制表示）
总共需要 19 bits，也是 2 个字节多一点，并且解码没有问题了，行不行？

这回解码没问题了，但并非最少字节，因为 c 的出现频率高（7 次）a 的出现频率低（1 次），因此出现频率高的字符编码成短数字更经济

考察下面的树

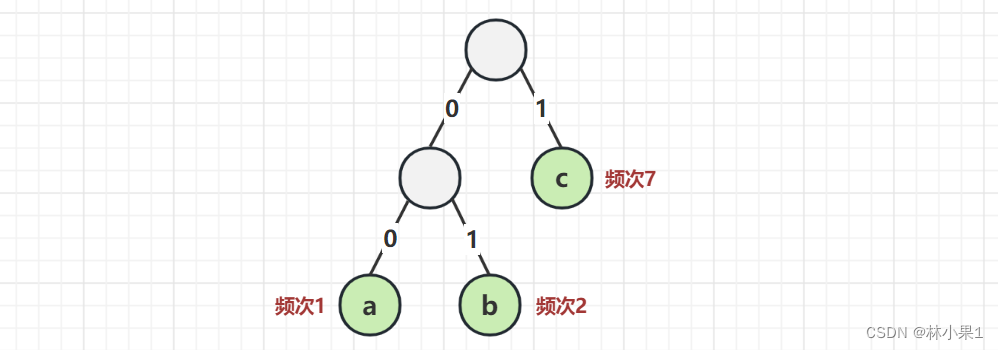
请添加图片描述

00 表示 a
01 表示 b
1 表示 c

现在还是传递 abbccccccc 这 10 个字符

实际的字节为 000101 1111111 （二进制表示）
总共需要 13 bits，这棵树就称之为 Huffman 树
根据 Huffman 树对字符和数字进行编解码，就是 Huffman 编解码

Huffman 树

public class HuffmanTree {

    Node root;
    String code;
    private static class Node{
        char ch;
        int freq;
        String code;
        Node left;
        Node right;

        public Node(char ch) {
            this.ch = ch;
        }

        public Node(char ch, int freq) {
            this.ch = ch;
            this.freq = freq;
        }

        public Node(int freq, Node left, Node right) {
            this.freq = freq;
            this.left = left;
            this.right = right;
        }

        public boolean isLeaf(){
            return this.left == null && this.right == null;
        }
    }

    public HuffmanTree(String s){
        char[] charArray = s.toCharArray();
        Map<String,Integer> map = new HashMap();
        for (char c : charArray) {
            Integer i = map.getOrDefault(String.valueOf(c),0);
            map.put(String.valueOf(c),i+1);
        }
        PriorityQueue<Node> queue = new PriorityQueue<>(Comparator.comparingInt(v -> v.freq));
        for (String string : map.keySet()) {
            Node node = new Node(string.charAt(0), map.get(string));
            queue.add(node);
        }
        while(queue.size() > 1){
            Node n1 = queue.poll();
            Node n2 = queue.poll();
            Node node = new Node(n1.freq + n2.freq, n1, n2);
            queue.add(node);
        }
        root = queue.peek();
        s = doEncode(root,new StringBuilder(),s);
        code = s;
    }
}

Huffman 编解码

补充两个方法，注意为了简单期间用了编解码都用字符串演示，实际应该按 bits 编解码

public class HuffmanTree {
    // ...

    // 编码
    private String doEncode(Node node,StringBuilder sb,String s){
        if(!node.isLeaf()){
            s = doEncode(node.left,sb.append(0),s);
            sb.deleteCharAt(sb.length()-1);
            s = doEncode(node.right,sb.append(1),s);
            sb.deleteCharAt(sb.length()-1);
        }else{
            node.code = sb.toString();
            while(s.contains(String.valueOf(node.ch))){
                s = s.replace(String.valueOf(node.ch), node.code);
            }
        }
        return s;
    }

    public String encode(){
        return code;
    }

    public String decode(String code){
        Node node = root;
        StringBuilder sb = new StringBuilder();
        char[] charArray = code.toCharArray();
        for (int i = 0; i < charArray.length; i++) {
            if(charArray[i] == '0'){
                node = node.left;
            }else {
                node = node.right;
            }
            if(node.isLeaf()){
                sb.append(node.ch);
                node = root;
            }
        }
        return sb.toString();
    }

    public static void main(String[] args) {
        HuffmanTree tree = new HuffmanTree("aabcccccc");
        String encode = tree.encode();
        System.out.println(encode);
        String decode = tree.decode(encode);
        System.out.println(decode);
    }
}