算法：

首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

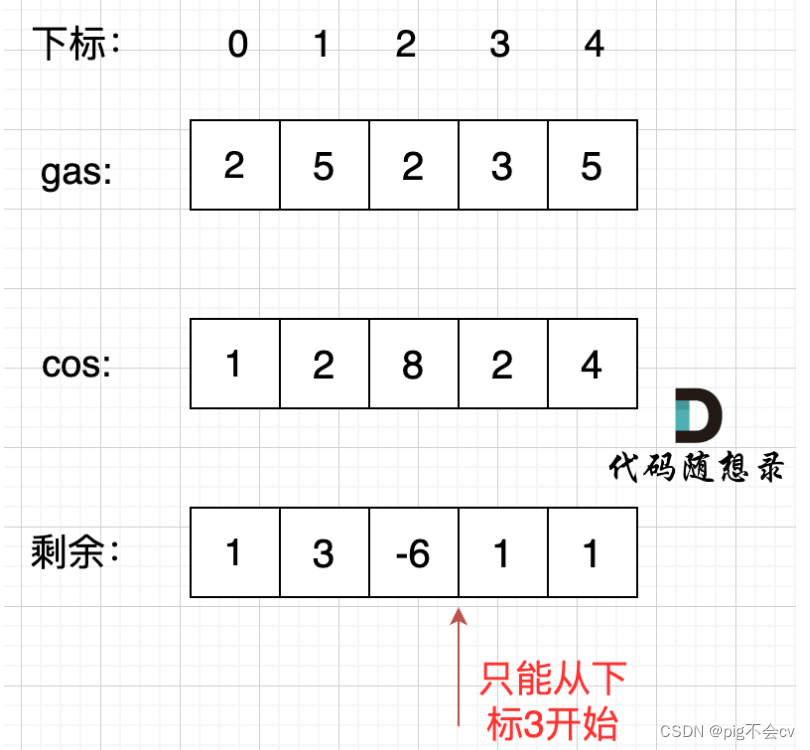
i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，

因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

局部最优：

当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。

全局最优：

找到可以跑一圈的起始位置。

那么为什么一旦[0，i] 区间和为负数，起始位置就可以是i+1呢，i+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新i，那么起始位置又变成新的i+1了。

正确代码：

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int cursum = 0;
        int totalsum = 0;
        int index = 0;
        for (int i = 0; i<gas.length; i++){
            cursum += gas[i] - cost[i];
            totalsum += gas[i] - cost[i];
//一旦[0，i] 区间和为负数，起始位置就是i+1
            if (cursum < 0){
                index = i+1;
                cursum = 0;
            }
        }
        if (totalsum < 0) return -1;
        return index;

    }
}

时间空间复杂度：

• 时间复杂度：O(n)。for循环遍历了整个数组，数组长度为n。
• 空间复杂度：O(1)