EfficientNet系列的模型在我们前面开发识别类项目或者是检测类项目都是比较少去使用的,一方面是技术本身迭代发展的速度是比较快的,可能新的东西还没学习更新的东西就出来了,另一方面是EfficientNet本身实际业务使用度并不高,可能真正项目开发落地过程中还需要解决额外的问题。
最近正好项目中在做一些识别相关的内容,我也陆陆续续写了一些实验性质的博文用于对自己使用过的模型进行真实数据的评测对比分析,感兴趣的话可以自行移步阅读即可:
《移动端轻量级模型开发谁更胜一筹,efficientnet、mobilenetv2、mobilenetv3、ghostnet、mnasnet、shufflenetv2驾驶危险行为识别模型对比开发测试》
《图像识别模型哪家强?19款经典CNN模型实践出真知【以眼疾识别数据为基准,对比MobileNet系列/EfficientNet系列/VGG系列/ResNet系列/i、xception系列】》
《基于轻量级卷积神经网络模型实践Fruits360果蔬识别——自主构建CNN模型、轻量化改造设计lenet、alexnet、vgg16、vgg19和mobilenet共六种CNN模型实验对比分析》
《基于轻量级模型GHoshNet开发构建眼球眼疾识别分析系统,构建全方位多层次参数对比分析实验》
本文的主要目的是想要以基准数据集【中草药图像数据集】为例,开发构建EfficientNet全系列不同参数量级的模型,之后在同样的测试数据集上进行评测对比分析。
数据集中共包含23种类别数据,清单如下:
aiye
baibiandou
baibu
baidoukou
baihe
cangzhu
cansha
dangshen
ezhu
foshou
gancao
gouqi
honghua
hongteng
huaihua
jiangcan
jingjie
jinyinhua
mudanpi
niubangzi
zhuling
zhuru
zhuye
zicao
简单看下部分数据实例:




EfficientNet是由谷歌研究团队提出的一种高效的卷积神经网络(CNN)架构,其构建原理基于网络深度、网络宽度和分辨率缩放的均衡策略:
1、网络深度:EfficientNet采用了复合系数(compound scaling)的思想,通过增加网络深度来提高其表达能力。复合系数是一个复合的缩放因子,将网络的深度、宽度和分辨率进行关联调整,以实现更好的性能。增加网络深度可以提高模型的表示能力,帮助模型更好地学习复杂的特征和模式。
2、网络宽度:在网络宽度方面,EfficientNet采用了通道缩放(channel scaling)的方法,通过调整每个卷积层的通道数来提高模型的表达能力。通道缩放可以在不增加过多参数的情况下提高模型的性能,使其更有效地利用计算资源。
3、分辨率缩放:EfficientNet通过分辨率缩放来调整输入图像的分辨率,以改善模型对不同尺度下的特征的学习能力。将输入图像的分辨率调整为适当的大小,可以使模型更好地适应不同尺度的特征,并提高在输入图像分辨率较高时的性能。
在构建EfficientNet时,研究团队通过对网络深度、宽度和分辨率的均衡性进行优化,提出了一种更高效的神经网络模型。经过复合系数的调整,EfficientNet在提高性能的同时也考虑了模型的计算效率,使其在训练速度和推断速度方面都表现出了很好的性能。总的来说,EfficientNet的构建原理可以概括为通过复合系数调整网络深度、宽度和分辨率,以实现在提高性能的同时保持计算效率。这种均衡策略使EfficientNet成为一种高效的深度学习模型,在图像识别等任务中取得了优秀的表现。
EfficientNet系列模型共构建了从B0到B7八个不同参数量级的模型,开源社区里面也有很多优秀的实现可以根据自己的实际需求选择即可,下面是我自己使用的keras实现的版本,如下所示:
def EfficientNet(
input_shape,
block_args_list: List[BlockArgs],
width_coefficient: float,
depth_coefficient: float,
include_top=True,
weights=None,
input_tensor=None,
pooling=None,
classes=1000,
dropout_rate=0.0,
drop_connect_rate=0.0,
batch_norm_momentum=0.99,
batch_norm_epsilon=1e-3,
depth_divisor=8,
min_depth=None,
data_format=None,
default_size=None,
**kwargs
):
if data_format is None:
data_format = K.image_data_format()
if data_format == "channels_first":
channel_axis = 1
else:
channel_axis = -1
if default_size is None:
default_size = 224
if block_args_list is None:
block_args_list = get_default_block_list()
stride_count = 1
for block_args in block_args_list:
if block_args.strides is not None and block_args.strides[0] > 1:
stride_count += 1
min_size = int(2**stride_count)
input_shape = _obtain_input_shape(
input_shape,
default_size=default_size,
min_size=min_size,
data_format=data_format,
require_flatten=include_top,
weights=weights,
)
if input_tensor is None:
inputs = layers.Input(shape=input_shape)
else:
if not K.is_keras_tensor(input_tensor):
inputs = layers.Input(tensor=input_tensor, shape=input_shape)
else:
inputs = input_tensor
x = inputs
x = layers.Conv2D(
filters=round_filters(32, width_coefficient, depth_divisor, min_depth),
kernel_size=[3, 3],
strides=[2, 2],
kernel_initializer=EfficientNetConvInitializer(),
padding="same",
use_bias=False,
)(x)
x = layers.BatchNormalization(
axis=channel_axis, momentum=batch_norm_momentum, epsilon=batch_norm_epsilon
)(x)
x = Swish()(x)
num_blocks = sum([block_args.num_repeat for block_args in block_args_list])
drop_connect_rate_per_block = drop_connect_rate / float(num_blocks)
for block_idx, block_args in enumerate(block_args_list):
assert block_args.num_repeat > 0
block_args.input_filters = round_filters(
block_args.input_filters, width_coefficient, depth_divisor, min_depth
)
block_args.output_filters = round_filters(
block_args.output_filters, width_coefficient, depth_divisor, min_depth
)
block_args.num_repeat = round_repeats(block_args.num_repeat, depth_coefficient)
x = MBConvBlock(
block_args.input_filters,
block_args.output_filters,
block_args.kernel_size,
block_args.strides,
block_args.expand_ratio,
block_args.se_ratio,
block_args.identity_skip,
drop_connect_rate_per_block * block_idx,
batch_norm_momentum,
batch_norm_epsilon,
data_format,
)(x)
if block_args.num_repeat > 1:
block_args.input_filters = block_args.output_filters
block_args.strides = [1, 1]
for _ in range(block_args.num_repeat - 1):
x = MBConvBlock(
block_args.input_filters,
block_args.output_filters,
block_args.kernel_size,
block_args.strides,
block_args.expand_ratio,
block_args.se_ratio,
block_args.identity_skip,
drop_connect_rate_per_block * block_idx,
batch_norm_momentum,
batch_norm_epsilon,
data_format,
)(x)
x = layers.Conv2D(
filters=round_filters(1280, width_coefficient, depth_coefficient, min_depth),
kernel_size=[1, 1],
strides=[1, 1],
kernel_initializer=EfficientNetConvInitializer(),
padding="same",
use_bias=False,
)(x)
x = layers.BatchNormalization(
axis=channel_axis, momentum=batch_norm_momentum, epsilon=batch_norm_epsilon
)(x)
x = Swish()(x)
if include_top:
x = layers.GlobalAveragePooling2D(data_format=data_format)(x)
if dropout_rate > 0:
x = layers.Dropout(dropout_rate)(x)
x = layers.Dense(classes, kernel_initializer=EfficientNetDenseInitializer())(x)
x = layers.Activation("softmax")(x)
else:
if pooling == "avg":
x = layers.GlobalAveragePooling2D()(x)
elif pooling == "max":
x = layers.GlobalMaxPooling2D()(x)
outputs = x
if input_tensor is not None:
inputs = get_source_inputs(input_tensor)
model = Model(inputs, outputs)
return model
训练集占比75%,测试集占比25%,所有模型按照相同的数据集配比进行实验对比分析,计算准确率、精确率、召回率和F1值四种指标。结果详情如下所示:
{
"EfficientNetB0": {
"accuracy": 0.7323568575233023,
"precision": 0.7342840951689299,
"recall": 0.7401447749844765,
"f1": 0.721134606264584
},
"EfficientNetB1": {
"accuracy": 0.6711051930758988,
"precision": 0.674815403573669,
"recall": 0.6814607103125642,
"f1": 0.654513293295677
},
"EfficientNetB2": {
"accuracy": 0.6804260985352862,
"precision": 0.6887820209389782,
"recall": 0.693270915541022,
"f1": 0.6667803713033284
},
"EfficientNetB3": {
"accuracy": 0.6577896138482025,
"precision": 0.6575815350378532,
"recall": 0.6697388006766206,
"f1": 0.6394242217002369
},
"EfficientNetB4": {
"accuracy": 0.607190412782956,
"precision": 0.6009338789436689,
"recall": 0.6201496013702704,
"f1": 0.575676812729165
},
"EfficientNetB5": {
"accuracy": 0.3754993342210386,
"precision": 0.4126647746126044,
"recall": 0.3840962856358272,
"f1": 0.33776556111562969
},
"EfficientNetB6": {
"accuracy": 0.29427430093209058,
"precision": 0.3007763995135063,
"recall": 0.3057837376695735,
"f1": 0.23015536725242517
},
"EfficientNetB7": {
"accuracy": 0.19573901464713715,
"precision": 0.1291924114976619,
"recall": 0.1938956570492365,
"f1": 0.10902900005697842
}
}简单介绍下上述使用的四种指标:
准确率(Accuracy):即分类器正确分类的样本数占总样本数的比例,通常用于评估分类模型的整体预测能力。计算公式为:准确率 = (TP + TN) / (TP + TN + FP + FN),其中 TP 表示真正例(分类器将正例正确分类的样本数)、TN 表示真负例(分类器将负例正确分类的样本数)、FP 表示假正例(分类器将负例错误分类为正例的样本数)、FN 表示假负例(分类器将正例错误分类为负例的样本数)。
精确率(Precision):即分类器预测为正例中实际为正例的样本数占预测为正例的样本数的比例。精确率评估分类器在预测为正例时的准确程度,可以避免过多地预测假正例。计算公式为:精确率 = TP / (TP + FP)。
召回率(Recall):即分类器正确预测为正例的样本数占实际为正例的样本数的比例。召回率评估分类器在实际为正例时的识别能力,可以避免漏掉过多的真正例。计算公式为:召回率 = TP / (TP + FN)。
F1 值(F1-score):综合考虑精确率和召回率,是精确率和召回率的调和平均数。F1 值在评估分类器综合表现时很有用,因为它同时关注了分类器的预测准确性和识别能力。计算公式为:F1 值 = 2 * (精确率 * 召回率) / (精确率 + 召回率)。 F1 值的取值范围在 0 到 1 之间,值越大表示分类器的综合表现越好。
为了能够直观清晰地对比不同模型的评测结果,这里对其进行可视化分析,如下所示:
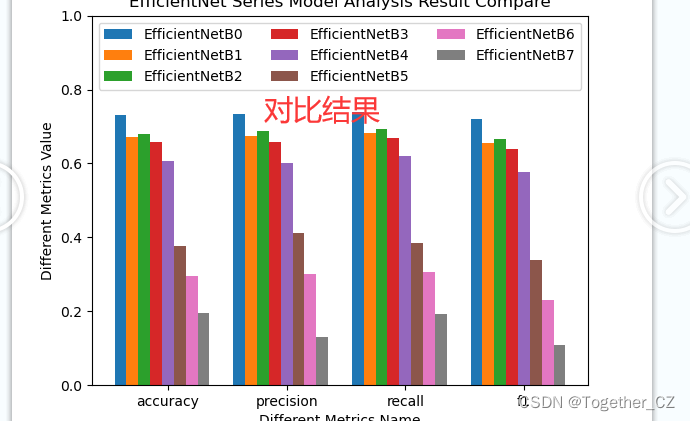
这个结果着实是没有预想到的,参数量更大的B7模型反而得到的效果是最差的,这个可能也跟我的显存太小跑B7的时候调小了很多Batch_size,但是感觉这个也不应该会差这么多,总之就是结果反映出来的问题很奇怪,后面有时间选择别的数据集再去尝试一下看看是不是都是这个情况。