Pytorch线性代数

news2024/11/17 1:53:27

1、加法运算

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
A, A + B

# tensor([[ 0.,  1.,  2.,  3.],
#          [ 4.,  5.,  6.,  7.],
#          [ 8.,  9., 10., 11.],
#          [12., 13., 14., 15.],
#          [16., 17., 18., 19.]]),

#  tensor([[ 0.,  2.,  4.,  6.],
#          [ 8., 10., 12., 14.],
#          [16., 18., 20., 22.],
#          [24., 26., 28., 30.],
#          [32., 34., 36., 38.]])

2、乘法运算

A * B
# tensor([[  0.,   1.,   4.,   9.],
#         [ 16.,  25.,  36.,  49.],
#         [ 64.,  81., 100., 121.],
#         [144., 169., 196., 225.],
#         [256., 289., 324., 361.]])

将张量乘以或加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。

import torch

a = 2
X = torch.arange(24).reshape(2, 3, 4)
print(X)
# tensor([[[ 0,  1,  2,  3],
#          [ 4,  5,  6,  7],
#          [ 8,  9, 10, 11]],

#         [[12, 13, 14, 15],
#          [16, 17, 18, 19],
#          [20, 21, 22, 23]]])

print((a + X).shape)
# torch.Size([2, 3, 4])

print(a + X)
# tensor([[[ 2,  3,  4,  5],
#          [ 6,  7,  8,  9],
#          [10, 11, 12, 13]],

#         [[14, 15, 16, 17],
#          [18, 19, 20, 21],
#          [22, 23, 24, 25]]])

3、降维

可以计算任意形状张量的元素和。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

print(A.sum())
# tensor(190.)

指定张量沿哪一个轴来通过求和降低维度。

为了通过求和所有行的元素来降维（轴0），可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量，因此输入轴0的维数在输出形状中消失。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

A_sum_axis0 = A.sum(axis=0)
print(A_sum_axis0)
# tensor([40., 45., 50., 55.])

A_sum_axis0 = A.sum(axis=1)
print(A_sum_axis0)
# tensor([ 6., 22., 38., 54., 70.])

沿着行和列对矩阵求和，等价于对矩阵的所有元素进行求和。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

print(A.sum(axis=[0, 1]))
# tensor(190.)

平均值通过将总和除以元素总数来计算平均值。 

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

print(A.mean())
# tensor(9.5000)

print(A.sum() / A.numel())
# tensor(9.5000)

计算平均值的函数也可以沿指定轴降低张量的维度。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

print(A.mean(axis=0))
# tensor([ 8.,  9., 10., 11.])

print(A.sum(axis=0) / A.shape[0])
# tensor([ 8.,  9., 10., 11.])

4、非降维求和

有时在调用函数来计算总和或均值时保持轴数不变会很有用。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

sum_A = A.sum(axis=1, keepdims=True)

print(sum_A)
# tensor([[ 6.],
#         [22.],
#         [38.],
#         [54.],
#         [70.]])

由于sum_A在对每行进行求和后仍保持两个轴，可以通过广播将A除以sum_A。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

sum_A = A.sum(axis=1, keepdims=True)
# tensor([[ 6.],
#         [22.],
#         [38.],
#         [54.],
#         [70.]])

print(A / sum_A)
# tensor([[0.0000, 0.1667, 0.3333, 0.5000],
#         [0.1818, 0.2273, 0.2727, 0.3182],
#         [0.2105, 0.2368, 0.2632, 0.2895],
#         [0.2222, 0.2407, 0.2593, 0.2778],
#         [0.2286, 0.2429, 0.2571, 0.2714]])

沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

print(A.cumsum(axis=0))
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  6.,  8., 10.],
#         [12., 15., 18., 21.],
#         [24., 28., 32., 36.],
#         [40., 45., 50., 55.]])

5、点积

torch.dot(x,y) 点积是两个向量相同位置的按元素乘积的和。

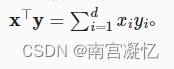
import torch

x = torch.arange(4, dtype=torch.float32)
print(x)
# tensor([0., 1., 2., 3.])

y = torch.ones(4, dtype = torch.float32)
print(y)
# tensor([1., 1., 1., 1.])

print(torch.dot(x, y))
# tensor(6.)

也可以通过执行按元素乘法，然后进行求和来表示两个向量的点积。

import torch

x = torch.arange(4, dtype=torch.float32)
print(x)
# tensor([0., 1., 2., 3.])

y = torch.ones(4, dtype = torch.float32)
print(y)
# tensor([1., 1., 1., 1.])

print(torch.sum(x * y))
# tensor(6.)

6、矩阵-向量积

将矩阵A用它的行向量表示

每个ai⊤都是行向量，表示矩阵的第i行。

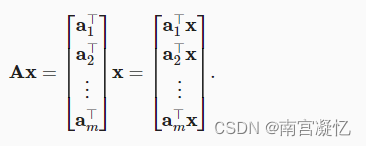
import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

x = torch.arange(4, dtype=torch.float32)
print(x)
# tensor([0., 1., 2., 3.])

print(torch.mv(A, x))
# tensor([ 14.,  38.,  62.,  86., 110.])

7、矩阵-矩阵乘法

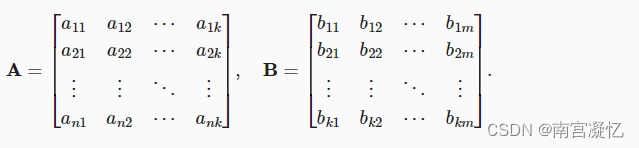
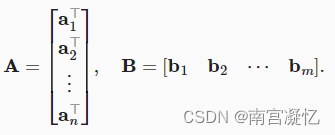ai行向量， bj列向量。

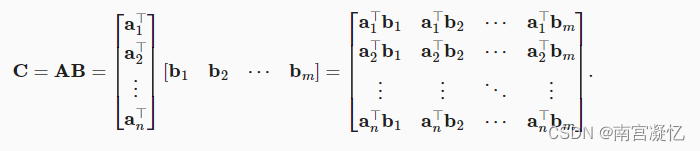
import torch

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
print(A)
# tensor([[ 0.,  1.,  2.,  3.],
#         [ 4.,  5.,  6.,  7.],
#         [ 8.,  9., 10., 11.],
#         [12., 13., 14., 15.],
#         [16., 17., 18., 19.]])

B = torch.ones(4, 3)
print(B)
# tensor([[1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.]])

print(torch.mm(A, B))
# tensor([[ 6.,  6.,  6.],
#         [22., 22., 22.],
#         [38., 38., 38.],
#         [54., 54., 54.],
#         [70., 70., 70.]])

8、范数

向量的范数是表示一个向量有多大。这里考虑的大小（size）概念不涉及维度，而是分量的大小。

向量范数是将向量映射到标量的函数f。

给定任意向量X，向量范数要满足一些属性。

第一个性质是：如果我们按常数因子a缩放向量的所有元素， 其范数也会按相同常数因子的绝对值缩放：

第二个性质是熟悉的三角不等式:

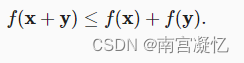
第三个性质简单地说范数必须是非负的:

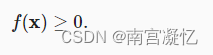
L2范数是向量元素平方和的平方根（向量）

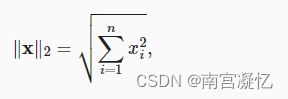
import torch

u = torch.tensor([3.0, -4.0])
print(torch.norm(u))
# tensor(5.)

L1范数是向量元素的绝对值

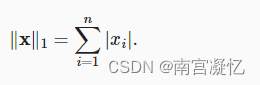
import torch

u = torch.tensor([3.0, -4.0])
print(torch.abs(u).sum())
# tensor(7.)

Lp一般范数

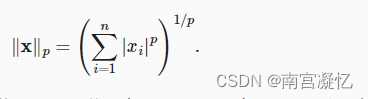
Frobenius范数是矩阵元素平方和的平方根（矩阵的L2范数）

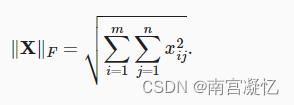
import torch

z = torch.ones((4, 9))
# tensor([[1., 1., 1., 1., 1., 1., 1., 1., 1.],
#         [1., 1., 1., 1., 1., 1., 1., 1., 1.],
#         [1., 1., 1., 1., 1., 1., 1., 1., 1.],
#         [1., 1., 1., 1., 1., 1., 1., 1., 1.]])

print(torch.norm(z))
# tensor(6.)
# (9*4)^(1/2)

范数和目标

在深度学习中，我们经常试图解决优化问题： 

  • 最大化分配给观测数据的概率; 
  • 最小化预测和真实观测之间的距离。

用向量表示物品（如单词、产品或新闻文章），以便最小化相似项目之间的距离，最大化不同项目之间的距离。

目标是深度学习算法最重要的组成部分（除了数据），通常被表达为范数。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1407780.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【裁员潮】技术变革下的职业危机，程序员会有多大影响，又应该如何面对

【裁员潮】技术变革下的职业危机，程序员会有多大影响，又应该如何面对

大家好，我是全栈小5，欢迎阅读文章！ 此篇是【话题达人】序列文章，这一次的话题是《技术变革下的裁员潮》 文章将以博主的角度进行讲述，理解和水平有限，不足之处，望指正。 目录 背景硬实力职业危机…
阅读更多...
Python环境的安装和Pycharm的安装

Python环境的安装和Pycharm的安装

Python环境的安装 英文版官网：Welcome to Python.org， 因为是外网，加载可能会很慢 首先呢，我们先去官网查找：Python中文网 官网，这个官网是中文版的，点进去之后是这个页面 然后点击下载&#…
阅读更多...
【nowcoder】链表的回文结构

【nowcoder】链表的回文结构

牛客题目链接 链表的回文结构 /* struct ListNode {int val;struct ListNode *next;ListNode(int x) : val(x), next(NULL) {} };*/ #include <cstdlib> // 建议大伙自己对照我的代码画下图&#xff0c;假设A链表是&#xff1a;1 2 3 2 1 class PalindromeList { publi…
阅读更多...
消息队列RabbitMQ.02.交换机的讲解与使用

消息队列RabbitMQ.02.交换机的讲解与使用

目录 RabbitMQ中交换机的基本概念与作用解析 交换机的作用&#xff1a; 交换机的类型&#xff1a; 直连交换机&#xff08;Direct Exchange&#xff09;&#xff1a; 将消息路由到与消息中的路由键&#xff08;Routing Key&#xff09;完全匹配的队列。 主题交换机&#x…
阅读更多...
【计算机网络】UDP协议与TCP协议

【计算机网络】UDP协议与TCP协议

文章目录 一、端口号1.什么是端口号2.端口号范围划分3.认识知名端口号(Well-Know Port Number)4.netstat5.pidof 二、UDP协议1.UDP协议端格式2.UDP的特点3.面向数据报4.UDP的缓冲区5.UDP使用注意事项6.基于UDP的应用层协议 三、TCP协议1.TCP协议段格式1.1理解封装解包和分用1.2…
阅读更多...
数据结构（C语言版）代码实现（三）——单链表部分代码实现

数据结构（C语言版）代码实现（三）——单链表部分代码实现

目录 格式 头文件 宏定义 线性表的单链表存储结构 按位查找 插入元素 删除元素 头插法建立单链表 合并非递减单链表 其他基本操作 完整版 测试代码&#xff08;主函数&#xff09; 测试结果 格式 参考 2.3节 线性表的链式表示和实现 头文件 宏定义 #pragma onc…
阅读更多...
安卓移动设备使用DS file文件管理工具远程访问本地群晖NAS文件

安卓移动设备使用DS file文件管理工具远程访问本地群晖NAS文件

文章目录 1. 群晖安装Cpolar2. 创建TCP公网地址3. 远程访问群晖文件4. 固定TCP公网地址5. 固定TCP地址连接6. 结语 DS file 是一个由群晖公司开发的文件管理应用程序&#xff0c;主要用于浏览、访问和管理存储在群晖NAS&#xff08;网络附加存储&#xff09;中的文件。这个应用…
阅读更多...
小模型也能COT

小模型也能COT

前两章我们分别介绍了COT的多种使用方法以及COT的影响因素。这一章更多面向应用&#xff0c;既现实场景中考虑成本和推理延时&#xff0c;大家还是希望能用6B的模型就不用100B的大模型。但是在思维链基础和进阶玩法中反复提到不论是few-shot还是zero-shot的思维链能力似乎都是1…
阅读更多...
‘cnpm‘ 不是内部或外部命令,也不是可运行的程序

‘cnpm‘ 不是内部或外部命令,也不是可运行的程序

一、问题 昨天用npm 安装环境&#xff0c;实在太慢了&#xff0c;就想用cnpm&#xff0c;然后发现提示‘cnpm 不是内部或外部命令,也不是可运行的程序。 看了很多方法&#xff0c;选择了下面这个&#xff0c;运气好到爆棚&#xff0c;就直接可以用了。其他的方法暂未去了解。先…
阅读更多...
【极数系列】Flink 初相识（01）

【极数系列】Flink 初相识（01）

# 【极数系列】Flink 初相识&#xff08;01&#xff09; 引言 Flink官网&#xff1a;https://flink.apache.org/ Flink版本&#xff1a;https://flink.apache.org/blog/ Flink文档&#xff1a;https://ci.apache.org/projects/flink/flink-docs-release-1.12/ Flink代码库…
阅读更多...
shell脚本-条件测试、

shell脚本-条件测试、

一.条件测试 1.&#xff08; &#xff09; 和 { } &#xff08;&#xff09;会进/data ,开启子shell { } 直接切过去了&#xff0c;不开子shell 小案例&#xff1a; 2. test 命令 测试特定的表达式是否成立&#xff0c;当条件成立&#xff0c;测试语句的返回值为0&#xff…
阅读更多...
[BUG] Authentication Error

[BUG] Authentication Error

前言 给服务器安装了一个todesk&#xff0c;但是远程一直就是&#xff0c;点击用户&#xff0c;进入输入密码界面&#xff0c;还没等输入就自动返回了 解决 服务器是无桌面版本&#xff0c;或者桌面程序死掉了&#xff0c;重新安装就好 sudo apt install xorg sudo apt inst…
阅读更多...
PIL笔记：通道+模式+坐标系统+基本图像操作

PIL笔记：通道+模式+坐标系统+基本图像操作

PIL Python Imaging Library&#xff0c;Python的图像处理核心库 通道bands 灰度图片是单通道组成 彩色图片是三通道RGB组成 真彩色图片是四通道RGBA组成 模式 RGB RGBA … 坐标系统 左上角为原点(0, 0) 图像操作 显示图像 show 创建图像 open()打开图像new()创建I…
阅读更多...
嵌入式学习-C++-Day1

嵌入式学习-C++-Day1

嵌入式学习-CDay1 一、思维导图 二、作业 1.提示并输入一个字符串&#xff0c;统计该字符中大写、小写字母个数、数字个数、空格个数以及其他字符个数&#xff08;要求使用C风格字符串完成&#xff09; #include <iostream> #include <string.h>using namespace…
阅读更多...
shopee母婴选品：Shopee平台上进行母婴类目的选品

shopee母婴选品：Shopee平台上进行母婴类目的选品

在Shopee平台上进行母婴类目的选品时&#xff0c;卖家可以通过一些策略来提高产品的市场竞争力和销售业绩。下面将详细介绍这些策略。 先给大家推荐一款shopee知虾数据运营工具知虾免费体验地址&#xff08;复制浏览器打开&#xff09;&#xff1a;D。dDqbt。Com/JU5o知虾是Sh…
阅读更多...
考研C语言刷题基础篇之分支循环结构基础（二）

考研C语言刷题基础篇之分支循环结构基础（二）

目录 第一题分数求和 第二题&#xff1a;求10 个整数中最大值 第三题&#xff1a;在屏幕上输出9*9乘法口诀表 第四题&#xff1a;写一个代码&#xff1a;打印100~200之间的素数 第五题&#xff1a;求斐波那契数的第N个数 斐波那契数的概念&#xff1a;前两个数相加等于第三…
阅读更多...
3.Eureka注册中心

3.Eureka注册中心

3.Eureka注册中心 假如我们的服务提供者user-service部署了多个实例&#xff0c;如图&#xff1a; 大家思考几个问题&#xff1a; order-service在发起远程调用的时候&#xff0c;该如何得知user-service实例的ip地址和端口&#xff1f;有多个user-service实例地址&#xff0…
阅读更多...
git clone报错 fatal: unable to fork

git clone报错 fatal: unable to fork

1. 问题 git clone gitgithub.com:url-kaist/Quatro.git Cloning into Quatro... fatal: unable to fork 在使用Docker clone 代码时报错 2. 解决方法 查看是否安装openssh&#xff0c; 用以下命令查看系统是否已安装OpenSSH&#xff0c;如果有openssh-client和openssh-serve…
阅读更多...
Oracle、MySQL数据库常规命令语法-简易记录（非常规持续更新）

Oracle、MySQL数据库常规命令语法-简易记录（非常规持续更新）

前言：呈现的是非常基础必备命令以及常规关联语法，因涉及到不同数据库其表达都会有所区别，此篇纯属做个仓库记录更非常规持续更新，专业人士可忽略，且看且珍惜… MySQL: 关系型数据库、重点开源、支持大型规模、标准SQL数据语言、多平台多架构、高可用集群、可定制开发等…
阅读更多...
php基础学习之变量

php基础学习之变量

php使用变量的必要性 PHP 是一种动态网站开发的脚本语言&#xff0c;动态语言特点是交互性&#xff0c;会有数据的传递&#xff0c;而 PHP作为“中间人”&#xff0c;需要进行数据的传递&#xff0c;传递的前提就是 PHP 能自己存储数据(临时存储) php变量的命名规则 必须以do…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023