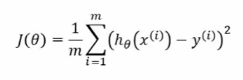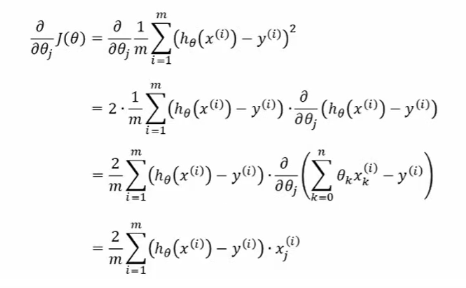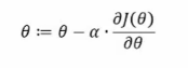文章目录
- 🧡🧡实验内容🧡🧡
- 🧡🧡数据预处理🧡🧡
- 代码
- 缺失值处理
- 特征探索
- 相关性分析
- 文本数据标签编码
- 数值型数据标准化
- 划分数据集
- 🧡🧡线性回归🧡🧡
- 闭合形式参数求解原理
- 梯度下降参数求解原理
- 代码
- 运行结果
- 🧡🧡总结🧡🧡
🧡🧡实验内容🧡🧡
基于California Housing Prices数据集,完成关于房价预测的线性回归模型训练、测试与评估。
🧡🧡数据预处理🧡🧡
代码
"""
数据预处理
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
df=pd.read_csv("data/housing.csv")
df.info()
### =====================填充缺失值=====================
print(df.isna().sum())
median_bedrooms = df['total_bedrooms'].median()
df['total_bedrooms'].fillna(median_bedrooms, inplace=True)
### =====================特征探索=====================
df.hist(bins=50,figsize=(20,15),edgecolor="black")
plt.show()
### =====================相关性分析=====================
corr_matrix=df.corr()
corr_matrix['median_house_value'].sort_values(ascending=False)
### =====================组合特征=====================
df['population_per_household']=df['population']/df['households'] # 每家有几个人
df['rooms_per_household']=df['total_rooms']/df['households'] # 每家有几个房屋
df['bedrooms_per_room']=df['total_bedrooms']/df['total_rooms'] # 每个房屋有几个卧室
# corr_matrix=df.corr()
# corr_matrix['median_house_value'].sort_values(ascending=False)
df.drop(["population","households","total_rooms","total_bedrooms"],axis=1,inplace=True)
### =====================文本型数据:独热编码=====================
df = pd.get_dummies(df, columns=['ocean_proximity'])
### =====================连续型数据:标准化=====================
df['income_copy']=df['median_income'] # 留着后面分层抽样
con_cols=['longitude','latitude','housing_median_age','median_income',
'population_per_household','rooms_per_household','bedrooms_per_room','median_house_value']
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
df[con_cols] = scaler.fit_transform(df[con_cols])
df
"""
划分数据集
"""
### =====================划分数据集:分层抽样=====================
# 将median_income这个连续数据映射分级,放到新属性income_cat中
df['income_cat'] = pd.cut(df['income_copy'],
bins=[0, 1.5, 3.0, 4.5, 6, np.inf],
labels=["1", "2", "3", "4", "5"])
df["income_cat"].hist(edgecolor="black", bins=11, grid=False)
# 分层抽样——按照income_cat属性中比例分层(它最接近符合正态分布)
from sklearn.model_selection import StratifiedShuffleSplit
ss=StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_idx, test_idx in ss.split(df, df['income_cat']):
train_strat=df.loc[train_idx]
test_strat=df.loc[test_idx]
print(f"train_len: {len(train_strat)}, test_len: {len(test_strat)}")
print("train 和 test 中 income_cat 比例: \n", train_strat["income_cat"].value_counts()/len(train_strat))
# 删除无用特征
df.drop(['latitude','longitude','median_house_value','income_copy','income_cat'],axis=1,inplace=True)
train_strat.drop(['income_cat','income_copy','latitude','longitude'],axis=1,inplace=True)
test_strat.drop(['income_cat','income_copy','latitude','longitude'],axis=1,inplace=True)
# 划分train和test
y_train=train_strat['median_house_value'].values # .values转array
x_train=train_strat.drop('median_house_value',axis=1).values
y_test=test_strat['median_house_value'].values
x_test=test_strat.drop('median_house_value',axis=1).values
缺失值处理
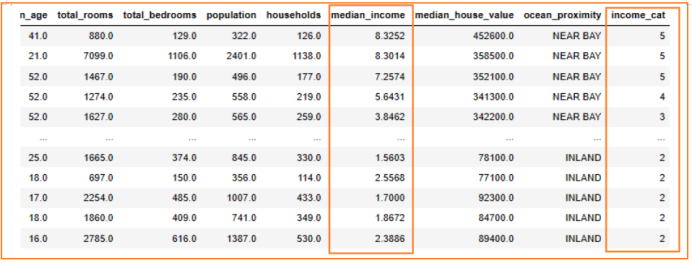
如下图,统计出total_bedrooms出现207个空值,而总样本数为20640个,大约占1%,因此可以考虑直接剔除,也可以替代,这里这个特征属于连续型变量,采用中位数替代。
特征探索
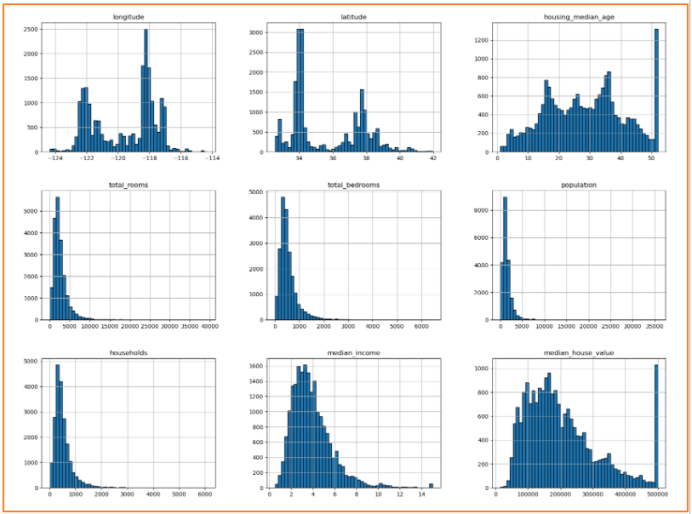
对数据集中的连续型特征绘制其直方图,总结出一些处理建议:
- 前两幅图为房地的经纬度,因此数值比较分散,不呈正态分布,情有可原
- total_rooms、total_bedrooms、population、households这几幅图很类似,同时考虑到其表达的含义比较相似,可以对它们考虑进行特征组合(后述)。另外,它们都呈现较偏左边的正态分布,右半部分比较空缺,可以考虑通过采样优化其分布(后述)。
- median_income比较接近理想的正态分布,在划分数据集时,可以考虑以它为基准进行分层抽样,这样也能保证total_rooms等特征分布呈较为合理的正态分布。
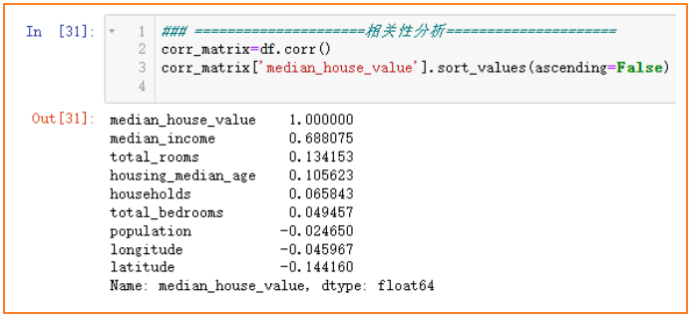
相关性分析
各个特征与房价median_house_value的相关性分析如下图,越接近1和-1越相关,0表示没有线性关系。可以看出收入median_income与房价呈很强的正相关关系,househols、total_bedrooms、popultion这几个特征对于房价来说相关性很小,结合前面特征探索中,可以将其组合出新的特征。例如
- 对于地区家庭数目households和总房屋数目total_rooms,组合成“每个家庭的房屋数量”更具有代表性。
- 对于地区卧室总数目total_bedrooms和总房屋总数目total_rooms,显然单知道两者数目比较空泛,现实生活中更看重“房间卧室的占比”,是一个衡量房价的重要指标
- 对于地区总人口和总家庭数目,可以尝试组合成“每个家庭有多少人”,可能可以从侧面反应出房间大小,进而体现房价。
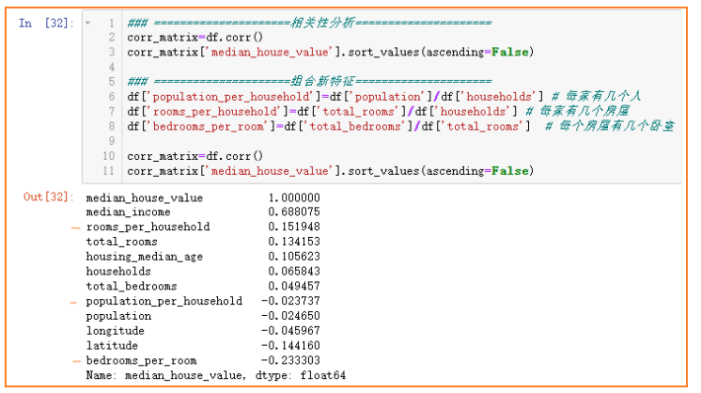
组合新特征出如下图,可以看到,新组合出的特征rooms_per_households和bedrooms_per_rom比原特征对于房价的相关性要更大,显然房间卧室的占比越小,房价越贵,符合事实。
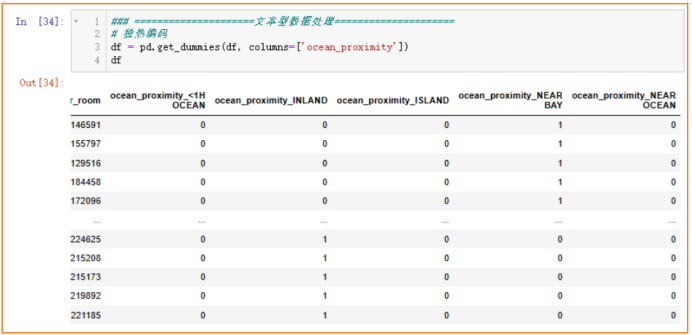
文本数据标签编码
对于地区举例海洋的距离ocean_proximity这个特征,虽然印象里认为“离海越近房价越高”(毕竟海景房更招人喜欢),考虑使用标签编码是不错的选择,但是这个特征值表示的仅是与海的距离分级,离海越接近不一定代表有更多客户青睐(毕竟能稍微远一点也能看到海景,还不用担心极端天气海边发生突发状况)。综合以上可能存在的不确定的主观因素,以及对于现实情况还不够太了解,我选择独热编码,让机器自行训练自行分辨。
数值型数据标准化
采用z-score标准化,对于每一列特征,均处理成(X-均值) / 方差。
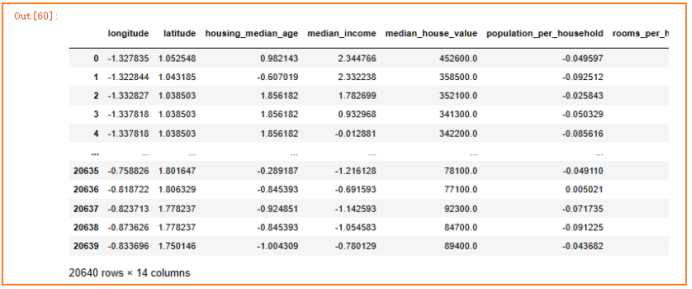
划分数据集
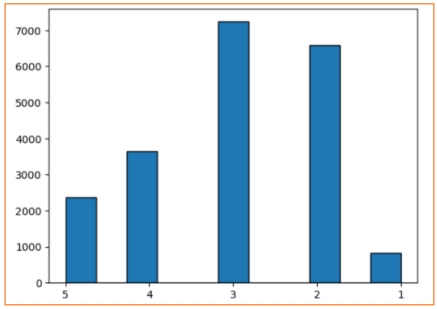
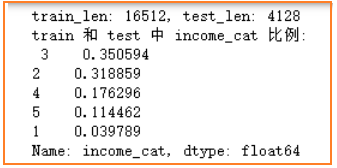
前面特征探索流程中,观察得出收入median_income最接近合理的正态分布,并且它与房价的相关性程度最大,因此依据不同收入median_income的等级比例来进行分层抽样。首先将连续型的收入median_income依据大小映射成不同的收入等级income_cat,并统计不同等级比例,然后依据这个等级比例分层抽样划分出训练集和测试集(即不管是在训练集和测试集中,数据比例满足收入等级对应的比例)。
🧡🧡线性回归🧡🧡
闭合形式参数求解原理
主要是通过最小化残差平方和来找到最优的回归系数
- 设要求的函数为
- 其中X为样本,θ为参数向量
- 代价函数表示为最小化残差平方和(预测值和真实值的误差):
- 对代价函数求导:
- 令导数为0:
得到如上线性回归模型的闭合形式解,能够直接计算出最优的回归系数,然而其中(XT*X)-1有时很难求解。
梯度下降参数求解原理
通过迭代优化,逐步调整回归系数以最小化损失函数,从而得到较优值对应的回归系数。
- 确定损失函数
- 计算梯度
- 梯度下降(负梯度方向)
其中α为下降的步幅(学习率),需提前设定。
重复计算梯度并且更新系数,直到达到预先设定的迭代次数或者损失函数收敛至某个阈值,本实验中通过设定每两次迭代中损失函数变化不超过1e-8,则认为损失函数收敛至某个阈值。
代码
### =====================指标评估函数=====================
def mean_absolute_error(y_true, y_pred):
return np.mean(np.abs(y_pred - y_true))
def mean_squared_error(y_true, y_pred):
return np.mean((y_pred - y_true) ** 2)
def root_mean_squared_error(y_true, y_pred):
return np.sqrt(mean_squared_error(y_true, y_pred))
def r_squared(y_true, y_pred):
y_mean = np.mean(y_true)
ss_total = np.sum((y_true - y_mean) ** 2)
ss_residual = np.sum((y_true - y_pred) ** 2)
r2 = 1 - (ss_residual / ss_total)
return r2
def goodness_of_fit(y_true, y_pred):
return np.sqrt(r_squared(y_true, y_pred))
### =====================求解=====================
import time
## 闭合式求解法
def close_solve(X,Y):
# np.linalg.inv求矩阵的逆, .T求矩阵的转置
theta=np.linalg.inv(X.T.dot(X)).dot(X.T).dot(Y)
return theta
start_time = time.time() # 记录程序开始时间
print("============闭合式求解:==========")
theta=close_solve(x_train, y_train)
print(f"theta: {theta}")
y_pred=np.dot(x_test,theta)
print("MAE:", mean_absolute_error(y_test, y_pred)) # 平均绝对误差
print("MSE:", mean_squared_error(y_test, y_pred)) # 均方误差
print("RMSE:", root_mean_squared_error(y_test, y_pred)) # 均方根误差
print("R方:", r_squared(y_test, y_pred)) # R方
print("拟合优度:", goodness_of_fit(y_test, y_pred)) # 拟合优度
print(f"===运行时间===:{time.time()-start_time} 秒\n")
## 梯度下降法求解
# 定义损失函数
def loss_func(y_true, y_pred):
return (1/2)*mean_squared_error(y_true,y_pred) # 1/2 MSE
def gradient_descent(x_train, y_train, lr):
n,m=x_train.shape # 样本数目
theta=np.zeros(m)
while True:
# 计算误差error和损失loss
y_pred=np.dot(x_train, theta)
error=y_pred - y_train
loss=loss_func(y_train, y_pred)
# 计算梯度、更新参数
gradient= 2 * np.dot(x_train.T, error) / n
theta-=lr*gradient
if len(loss_histroy)!=0 and abs( loss - loss_histroy[-1]) < 1e-8: #结束条件
break
loss_histroy.append(loss)
return theta
start_time = time.time() # 记录程序开始时间
loss_histroy=[]
print("============梯度下降法求解:============")
theta=gradient_descent(x_train, y_train, lr=0.01)
print(f"theta: {theta}")
y_pred=np.dot(x_test,theta)
print("MAE:", mean_absolute_error(y_test, y_pred)) # 平均绝对误差
print("MSE:", mean_squared_error(y_test, y_pred)) # 均方误差
print("RMSE:", root_mean_squared_error(y_test, y_pred)) # 均方根误差
print("R方:", r_squared(y_test, y_pred)) # R方
print("拟合优度:", goodness_of_fit(y_test, y_pred)) # 拟合优度
print(f"===运行时间===:{time.time()-start_time} 秒\n")
plt.plot(loss_histroy)
plt.xlabel("iter")
plt.ylabel("loss")
## print特征对应的参数
for f,t in zip(df.columns,theta):
print(f"{f}\t{t}")
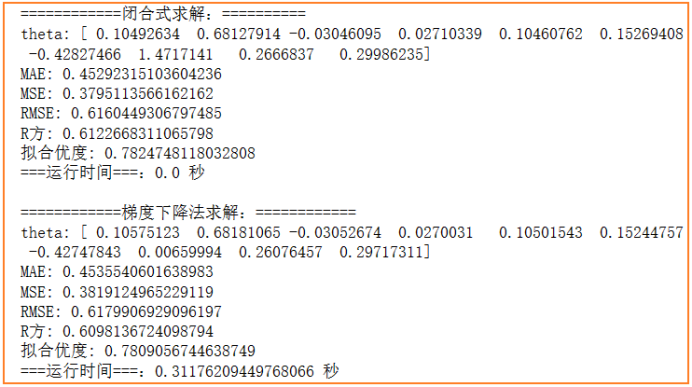
运行结果
通过闭合式求解和梯度下降法求解,并用MAE、MSE、RMSE、R方、拟合优度等来比较两种求解方式的求解效果如下
可以看见,两种方法得出的结果差别不大,总体来看,闭合式求解的误差(MAE、MSE、RMSE)相对小,拟合效果(R方、拟合优度)相对大,因此在本次实验中闭合式求解的效果整体优于梯度下降法。
另外,能明显从运行时间看出两者的计算速度差异,闭合式由于只需计算结果公式(XT*X)-1X^TY,而梯度下降法中需要不断迭代更新theta很多次才能得到较优解,所以一般来说闭合式会快得多;但本实验中特征维度还算不多,闭合式会比较快,如若特征维度增多,闭合式的求解效率会变得很艰难,而梯度下降法在高纬度中仍然能以很快的速度求解出较优值。
总结来说:
- 闭合式求解法在可解的情况下,一定能求解出全局最优解,但计算速度受维度影响大,当维度较大时,可能出现不可解的情况。
- 梯度下降法不一定能求解出最优解,但在高维度时计算速度仍然有可观的效果。
🧡🧡总结🧡🧡
讨论实验结果,分析各个特征与目标预测值的正负相关性
- 呈负相关性的特征:
对于population_per_household,实验结果表明平均家庭人口越少,可能意味着住房拥挤,家庭成员较多时,每个人的居住空间和私密性可能会减少,进而可能会间接降低该地区的房价,但相关性很小,只有0.03,接近0,因此可以认为这个特征实际上对于房价影响不大,改进实验时应该不再组合这个新特征。
对于ocean_proximity_INLAND,实验结果表明靠近内陆的地区房价会越低,且相关性程度达0.42,结合实际,内陆地区由于缺乏海洋景观等吸引力因素,房价则相对较低。
- 呈正相关性的特征:
相关性程度较大的主要是收入median_income,高达0.68,结合实际考虑,高收入人群通常更愿意支付更高的房价,因此高收入区域的房价往往更高。其次主要是与海洋远近的特征,结合实际考虑,靠近海湾和靠近海洋的地区往往景色优美、气候宜人,因此房价会相应较高。
剩余特征如房龄housing_median_age、卧室占比bedrooms_per_room等等,对房价的影响程度较小。