数据结构与算法——队列原理及C语言底层实现

news2024/10/6 8:40:01

数据结构与算法——队列原理及C语言底层实现

  • 队列概念
  • 顺序队列
    • 1. 顺序队列原理
    • 2. 队列的创建
    • 3. 入队与出队
    • 4. 判断满队与空队
    • 5. 清空队列与释放空间
    • 6. 主流程测试
  • 链式队列
    • 1. 链式队列的创建
    • 2. 链式队列入队
    • 3. 链式队列出队
    • 4. 判断是否为空队
    • 5. 清空队列与释放空间
    • 6. 主流程测试
  • 栈与队列综合应用——球钟问题

参考博文：【数据结构与算法】程序内功篇五–队列

队列概念

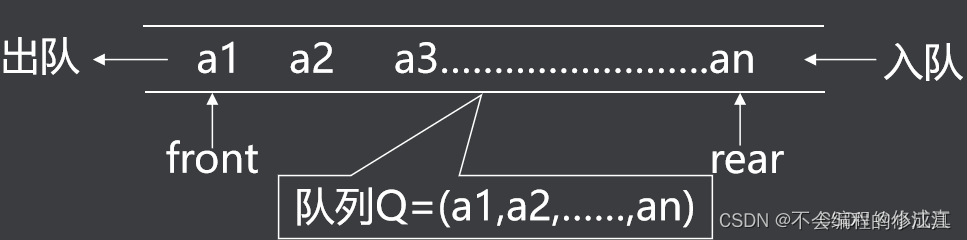
  • 队列是限制在两端进行插入操作和删除操作的线性表
  • 允许进行插入操作的一端称为“队尾”
  • 允许进行删除操作的一端称为“队头”
  • 当线性表中没有元素时，称为“空队”
  • 特点 ：先进先出（FIFO）

在这里插入图片描述

顺序队列

1. 顺序队列原理

  • 规定： front指向对头元素的位置，rear指向队尾元素的下一个位置
  • 在队列操作过程中，为了提高效率，以调整指针代替队列元素的移动，并将数组作为循环队列的操作空间。
  • 为区别空队和满队，满队元素个数比数组元素个数少一个。
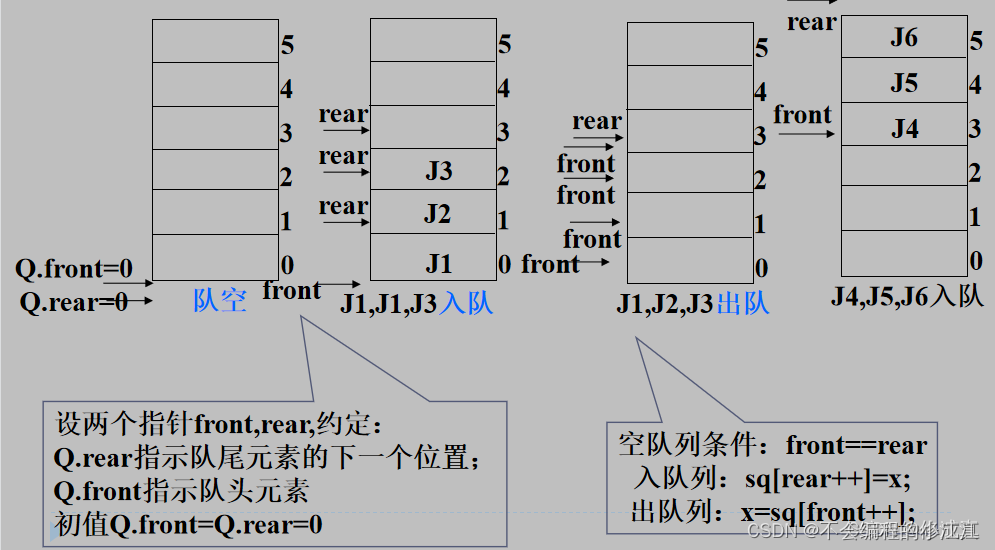
    在这里插入图片描述

因此顺序队列的结构体定义为：

typedef int data_t;		//定义栈中数据元素类型
#define N 64			//定义队列容量
//队列的定义
typedef struct{
	data_t  data[N];	//用数组作为队列的存储空间
	int front,rear;		//指示队头和队尾位置的指针
}sequeue_t;				//顺序队列类型定义

2. 队列的创建

①申请队列内存空间
②初始化数据
③设置队列头等于队列尾

//创建队列
sequeue* queue_create()
{
	sequeue *sq;
	
	//申请内存空间
	sq = (sequeue *)malloc(sizeof(sequeue));
	if(sq == NULL){
		printf("malloc sequeue failed\n");
		return NULL;
	}
	
	//初始化数据
	memset(sq->data, 0, sizeof(sq->data));
	
	//定义队列头尾为0
	sq->front = 0;
	sq->rear  = 0;
	
	return sq;
}

3. 入队与出队

3.1 入队
①参数检查与判断是否为满队
②队尾插入元素
③队尾指针偏移

//入队列 -1: 入队失败 	0 : 入队成功
int enqueue(sequeue *sq, data_t value)
{
	//入口参数检查
	if(sq == NULL){
		printf("sequeue is NULL\n");
		return -1;
	}
	
	//判断队列是否为满队列
	if((sq->rear+1) % N == sq->front){
		printf("sequeue is full\n");
		return -1;
	}
	
	//队尾存入元素
	sq->data[sq->rear] = value;
	sq->rear = (sq->rear + 1) % N;
	
	return 0;
}

3.2 出队
①参数检查与判断是否为空队
②获取队头元素
③队头指针偏移

//出队
data_t dequeue(sequeue *sq)
{
	//入口参数检查
	if(sq == NULL){
		printf("sequeue is NULL\n");
		return -1;
	}
	
	//空队
	if(sq->front == sq->rear){
		return -1;
	}
	
	//获取队头数据
	data_t ret;
	ret = sq->data[sq->front];			//队头数据
	sq->front = (sq->front + 1) % N;	//队头指针偏移
	return ret;
}

4. 判断满队与空队

4.1 判断是否为空队 ，空队：队头指针 = 队尾指针

//判断队列是否为空队列
// 1: 空队   0: 非空队  -1:参数异常
int queue_empty(sequeue *sq)
{
	//入口参数检查
	if(sq == NULL){
		printf("sequeue is NULL\n");
		return -1;
	}
	
	if(sq->front == sq->rear)
		return 1;
	else
		return 0;
}

4.2 判断是否为满队，满队：队头指针 = 队尾指针+1

//判断队列是否为满队列
// 1: 满队   0: 非满队  -1:参数异常
int queue_full(sequeue *sq)
{
	//入口参数检查
	if(sq == NULL){
		printf("sequeue is NULL\n");
		return -1;
	}
	
	//满队
	if((sq->rear + 1) % N == sq->front)
		return 1;
	else	
		return 0;
}

5. 清空队列与释放空间

5.1 清空队列

//清空队列
int queue_clear(sequeue *sq)		
{
	//入口参数检查
	if(sq == NULL){
		printf("sequeue is NULL\n");
		return -1;
	}
	
	sq->front = sq->rear = 0;
	return 0;
}

5.2 释放队列空间

//释放队列空间
sequeue* queue_free(sequeue *sq)	
{
	//入口参数检查
	if(sq == NULL){
		printf("sequeue is NULL\n");
		return NULL;
	}
	free(sq);
	sq = NULL;
}

6. 主流程测试

int main()
{
	sequeue *sq;
	sq = queue_create();
	if(sq == NULL)
		return -1;
	
	//入队
	enqueue(sq,1);
	enqueue(sq,2);
	enqueue(sq,3);
	enqueue(sq,4);

	while(!queue_empty(sq))				//队列不为空
	{
		printf("dequeue: %d\n",dequeue(sq));	//出队
	}
	queue_free(sq);			//释放队列
	return 0;
}

链式队列

  链式队列相当于就是在队尾插入，队头删除的链式结构，由队头指针和队尾指针控制队列的操作。
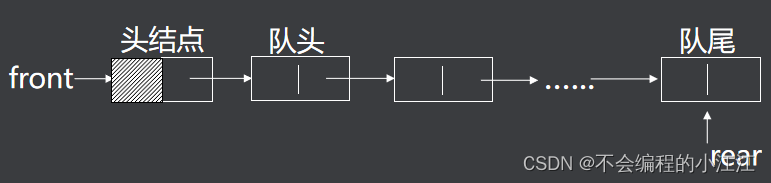
在这里插入图片描述

1. 链式队列的创建

①申请队列内存空间
②申请头尾节点空间
③节点数据赋值

//创建队列
linkqueue* queue_create()
{
    linkqueue *lq;

    //申请内存空间
    lq = (linkqueue *)malloc(sizeof(linkqueue));
    if(lq == NULL){
        printf("malloc linkqueue failed\n");
        return NULL;
    }

	//队列头尾指针申请内存空间
	linkqueue->front = linkqueue->rear = (listNode*)malloc(sizeof(listNode));
	if(linkqueue->front == NULL){
		printf("malloc listNode failed\n");
		return NULL;
	}

	//节点数据与指针赋值
	lq->front->data = 0;
	lq->front->next = NULL;

    return lq;
}

2. 链式队列入队

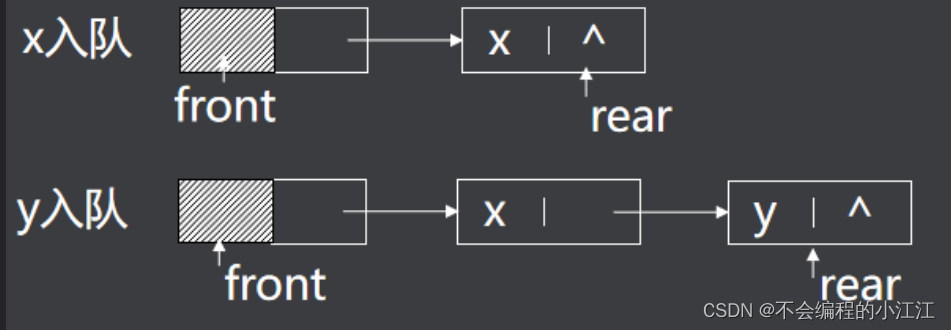
①封装孤立节点p
②队尾插入节点p
③更新队尾指针rear

//入队列 -1: 入队失败   0 : 入队成功
int enqueue(linkqueue *lq, data_t value)
{
    //入口参数检查
    if(lq == NULL){
        printf("linkqueue is NULL\n");
        return -1;
    }
	
	//1.封装孤立节点p
	listNode* p = (listNode*)malloc(sizeof(listNode));
	if(p == NULL){
		printf("malloc listNode failed\n");
		return -1;
    }
	p->data = value;
	p->next = NULL;

	//2.队尾插入节点p
	lq->rear->next = p;
	
	//3.更新队尾指针rear
	lq->rear = p;
	
    return 0;
}

3. 链式队列出队

①判断入口参数及是否为空队
②暂存待删除节点
③队头指针偏移
④释放空间

//出队
data_t dequeue(linkqueue *lq)
{
    //入口参数检查
    if(lq == NULL){
        printf("linkqueue is NULL\n");
        return -1;
    }

    //空队
    if(lq->front == lq->rear){
        return -1;
    }
	
	//暂存待删除节点并释放节点空间
	listNode* temp = lq->front;		//暂存队头节点
    lq->front = temp->next;   		//队头指针偏移
	free(temp);						//释放队头空间
	temp = NULL;
	
    return lq->front->data;
}

4. 判断是否为空队

空队：队头指针 = 队尾指针

//判断队列是否为空队列
// 1: 空队   0: 非空队  -1:参数异常
int queue_empty(linkqueue *lq)
{
    //入口参数检查
    if(lq == NULL){
        printf("linkqueue is NULL\n");
        return -1;
    }

    if(lq->front == lq->rear)
        return 1;
    else
        return 0;
}

5. 清空队列与释放空间

清空队列数据：

//清空队列
// -1: 函数失败，0: 函数成功
int queue_clear(linkqueue *lq)
{
    //入口参数检查
    if(lq == NULL){
        printf("linkqueue is NULL\n");
        return -1;
    }
	
	//判断队列是否为空队列
	if(lq->front == lq->rear){
		printf("linkqueue is empty\n");
		return -1;
	}
	
	//遍历链表，将数据初始化为0
	while(lq->front != NULL)
	{
		lq->front->data = 0;
		lq->front = lq->front->next;
	}
	
    return 0;
}

释放队列空间

//释放队列空间
int queue_free(linkqueue *lq)
{
    //入口参数检查
    if(lq == NULL){
        printf("linkqueue is NULL\n");
        return -1;
    }
	listNode * p;
	//循环释放节点
	while(lq->front)
	{
		p = lq->front;			//暂存节点
		lq->front = p->next;	//偏移队列头下标
		printf("free: %d\n",p->data);
		free(p);				//释放暂存节点
	}
	p = NULL; 
}

6. 主流程测试

int main()
{
	
    linkqueue *lq;
    lq = queue_create();
    if(lq == NULL)
        return -1;

    //入队
    enqueue(lq,1);
    enqueue(lq,2);
    enqueue(lq,3);
    enqueue(lq,4);
	
    while(!queue_empty(lq)) //队列不为空
    {
        printf("dequeue: %d\n",dequeue(lq));    //出队
    }
	
    queue_free(lq);         //释放队列

    return 0;
}

栈与队列综合应用——球钟问题

1、球钟简介
  球钟是一个利用球的移动来记录时间的简单装置，它有三个可以容纳若干个球的指示器：分钟指示器，五分钟指示器，小时指示器。若分钟指示器中有2个球，五分钟指示器中有6个球，小时指示器中有5个球，则时间为5:32

2、球钟工作原理

  • 每过一分钟，球钟就会从球队列的队首取出一个球放入分钟指示器，分钟指示器最多可容纳4个球。
  • 当放入第五个球时，在分钟指示器的4个球就会按照他们被放入时的相反顺序加入球队列的队尾。而第五个球就会进入五分钟指示器。
  • 按此类推，五分钟指示器最多可放11个球，小时指示器最多可放11个球。

3、问题阐述
  当小时指示器放入第12个球时，原来的11个球按照他们被放入时的相反顺序加入球队列的队尾，然后第12个球也回到队尾。这时，三个指示器均为空，回到初始状态，从而形成一个循环。因此，该球钟表示时间的范围是从0：00到11：59。
问题：
  现设初始时球队列的球数为27，球钟的三个指示器初态均为空。要经过多久，球队列才能恢复到原来的顺序？

4. 程序设计

#include <stdio.h>
#include "linkqueue.h"
#include "sqstack.h"

//检查队列是否升序
int check(linkqueue *lq);

int main()
{
	linkqueue* lq;		//队列名称
	int i;				//时钟球编号
	sqStack * stack_hour;	//定义三个栈容器
	sqStack * stack_five;
	sqStack * stack_min;
	int min = 0;		//分钟计时器
	int value;			//保存出队的值
	
	//创建链式队列
	lq = queue_create();   
	if(lq == NULL){
		printf("lq create failed\n");
		return -1;
	}
	//27个球顺序入队
	for(i = 1; i <= 27; i++)
		enqueue(lq, i);		

	//创建栈
	stack_hour = stack_create(11);
	stack_five = stack_create(11);
	stack_min  = stack_create(4);
	if(stack_hour == NULL || stack_five == NULL || stack_min == NULL){
		printf("create stack failed\n");
		return -1;
	}
	
	while(1)
	{
		min++;					//每过1分钟
		if(!queue_empty(lq))	//队不空
		{
			value = dequeue(lq);//出队
			
			//分钟计时器不满，放分钟计时器
			if(!stack_full(stack_min))
			{
				stack_push(stack_min,value);	//入分钟栈
			}
			else	//分钟计时器满
			{
				//栈不空 出栈入队列
				while(!stack_empty(stack_min))	
				{
					enqueue(lq, stack_pop(stack_min));
				}
				
				//5分钟计时器未满
				if(!stack_full(stack_five))
				{
					stack_push(stack_five, value);
				}
				else	//5分钟计时器满了 例如0:59
				{
					while(!stack_empty(stack_five))	//清空5分钟计时器
					{
						enqueue(lq, stack_pop(stack_five));	//出栈入队列
					}
					
					//小时计时器未满 小时计时器存入数据
					if(!stack_full(stack_hour))
					{
						stack_push(stack_hour, value);
					}
					else	//小时计时器也满了 11:59
					{
						while(!stack_empty(stack_hour))	//清空小时计时器
						{
							enqueue(lq, stack_pop(stack_hour));	//出栈入队列
						}
						enqueue(lq,value);		//栈全满，球放回队列
						//0:00
						if(check(lq) == 1)	//检查队列是否升序
						{
							break;
						}
					}
				}
			}		
		}
	}
	printf("total: %d\n",min);
	
	//队列不空 出队
	printf("dequeue: ");
	while(!queue_empty(lq))
	{
		printf("%d ",dequeue(lq));
	}
	printf("\n");
	
	return 0;
}


//检查队列是否升序
//1: 升序  0：无序
int check(linkqueue *lq)
{
	if(lq == NULL)
	{
		printf("lq is NULL\n");
		return 0;
	}
	
	listNode* p = lq->front->next;	//遍历队列
	while(p != NULL && p->next != NULL)
	{
		if(p->data < p->next->data)
			p = p->next;
		else	
			return 0;
	}
	return 1;
}

运行结果：

total: 33120
dequeue: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1406391.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

后端开发_单元测试

后端开发_单元测试

后端开发_单元测试 1. 简介2. JUnit 4使用方法2.1 jar包引入2.2 测试用例1. 简介 2. JUnit 4使用方法 2.1 jar包引入 1. 本地依赖引入方式 Junit4.jar包 2. maven方式引入jar <dep
阅读更多...
基于SSM的影视创作论坛（有报告）。Javaee项目。ssm项目。

基于SSM的影视创作论坛（有报告）。Javaee项目。ssm项目。

演示视频&#xff1a; 基于SSM的影视创作论坛&#xff08;有报告&#xff09;。Javaee项目。ssm项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系结构&#xff0c;通过Spring Spri…
阅读更多...
Sentinel 新版本发布，提升配置灵活性以及可观测配套

Sentinel 新版本发布，提升配置灵活性以及可观测配套

作者&#xff1a;屿山 基本介绍 Sentinel 是阿里巴巴集团开源的&#xff0c;面向分布式、多语言异构化服务架构的流量治理组件&#xff0c;承接了阿里巴巴近 15 年的双十一大促流量的核心场景&#xff0c;例如秒杀、冷启动、消息削峰填谷、集群流量控制、实时熔断下游不可用服…
阅读更多...
docker安装Rabbitmq教程（详细图文）

docker安装Rabbitmq教程（详细图文）

目录 1.下载Rabbitmq的镜像 2.创建并运行rabbitmq容器 3.启动web客户端 4.访问rabbitmq的微博客户端 5.遇到的问题 问题描述&#xff1a;在rabbitmq的web客户端发现界面会弹出如下提示框Stats in management UI are disabled on this node 解决方法 &#xff08;1&#…
阅读更多...
线程的同步和互斥学习笔记

线程的同步和互斥学习笔记

目录 互斥锁的概念和使用 线程通信-互斥 互斥锁的创建和销毁 申请锁-pthread_mutex_lock 释放锁-pthread_mutex_unlock 读写锁的概念和使用 死锁的避免 互斥锁的概念和使用 线程通信-互斥 临界资源 一次只允许一个任务&#xff08;进程、线程&#xff09;访问的共享资…
阅读更多...
Kubeadm安装单master多node节点K8S集群

Kubeadm安装单master多node节点K8S集群

kubeadm安装k8s1.25版本集群步骤 环境说明实验环境规划集群搭建规划 初始化安装k8s集群的实验环境安装虚拟机更新yum源和操作系统配置机器主机名配置主机hosts文件&#xff0c;相互之间通过主机名互相访问配置主机之间无密码登录关闭交换分区swap&#xff0c;提升性能修改机器内…
阅读更多...
漏洞补丁修复之openssl版本从1.1.1q升级到1.1.1t以及python版本默认2.7.5升级到2.7.18新版本和Nginx版本升级到1.24.0

漏洞补丁修复之openssl版本从1.1.1q升级到1.1.1t以及python版本默认2.7.5升级到2.7.18新版本和Nginx版本升级到1.24.0

​ 一、Openssl升级 1、查看Openssl安装的版本 openssl version 2、查看Openssl路径 which openssl 3、上传openssl安装包到服务器：openssl-1.1.1t.tar.gz，并且解压，安装： mv /usr/local/openssl /usr/local/backup_openssl_1.1.1q_20240120 mkdir /usr/local/openssl tar…
阅读更多...
LeetCode.2765. 最长交替子数组

LeetCode.2765. 最长交替子数组

题目 2765. 最长交替子数组 分析 为了得到数组 nums 中的最长交替子数组的长度&#xff0c;需要分别计算以每个下标结尾的最长交替子数组的长度。为了方便处理&#xff0c;计算过程中需要考虑长度等于 1 的最长交替子数组&#xff0c;再返回结果时判断最长交替子数组的长度…
阅读更多...
【AI视野·今日Robot 机器人论文速览 第七十五期】Thu, 11 Jan 2024

【AI视野·今日Robot 机器人论文速览 第七十五期】Thu, 11 Jan 2024

AI视野今日CS.Robotics 机器人学论文速览 Thu, 11 Jan 2024 Totally 16 papers &#x1f449;上期速览✈更多精彩请移步主页 Daily Robotics Papers Analytical Model and Experimental Testing of the SoftFoot: an Adaptive Robot Foot for Walking over Obstacles and Irre…
阅读更多...
MMagic调试（训练）dreambooth

MMagic调试（训练）dreambooth

时间&#xff1a;2024.1.23 1.dreambooth配置文件 dreambooth在mmagic中的路径&#xff1a; configs/dreambooth本文以dreambooth.py 为例 configs/dreambooth/dreambooth.py2.下载数据集 下载数据集并保存至data/dreambooth/&#xff0c;数据集&#xff1a; https://dri…
阅读更多...
[BUUCTF]-PWN:babyfengshui_33c3_2016解析

[BUUCTF]-PWN:babyfengshui_33c3_2016解析

又是一道堆题&#xff0c;先看保护 关键信息是32位&#xff0c;没开pie 直接看ida 大致是alloc创建堆块&#xff0c;free释放堆块&#xff0c;show查看堆块内容&#xff0c;fill填充堆块内容 其他的都没啥关键的要讲&#xff0c;但alloc那里非常需要解析一下 解释如上图 再具…
阅读更多...
npm install运行报错npm ERR! gyp ERR! not ok问题解决

npm install运行报错npm ERR! gyp ERR! not ok问题解决

执行npm install的时候报错&#xff1a; npm ERR! path D:..\node_modules\\**node-sass** npm ERR! command failed ...npm ERR! gyp ERR! node -v v20.11.0 npm ERR! gyp ERR! node-gyp -v v3.8.0 npm ERR! gyp ERR! not ok根据报错信息&#xff0c;看出时node-sass运行出现…
阅读更多...
基于taro搭建小程序多项目框架

基于taro搭建小程序多项目框架

前言 为什么需要这样一个框架&#xff0c;以及这个框架带来的好处是什么&#xff1f; 从字面意思上理解&#xff1a;该框架可以用来同时管理多个小程序&#xff0c;并且可以抽离公用组件或业务逻辑供各个小程序使用。当你工作中面临这种同时维护多个小程序的业务场景时&#xf…
阅读更多...
前端面试题-(浏览器内核，CSS选择器优先级，盒子模型，CSS硬件加速，CSS扩展）

前端面试题-(浏览器内核，CSS选择器优先级，盒子模型，CSS硬件加速，CSS扩展）

前端面试题-(浏览器内核&#xff0c;CSS选择器优先级&#xff0c;盒子模型&#xff0c;CSS硬件加速&#xff0c;CSS扩展&#xff09; 常见的浏览器内核CSS选择器优先级盒子模型CSS硬件加速CSS扩展 常见的浏览器内核 内核描述Trident(IE内核)主要用在window系统中的IE浏览器中&…
阅读更多...
【论文阅读|2024 WACV 多目标跟踪Deep-EloU】

【论文阅读|2024 WACV 多目标跟踪Deep-EloU】

论文阅读|2024 WACV 多目标跟踪Deep-EloU 摘要1 引言&#xff08;Introduction&#xff09;2 相关工作&#xff08;Related Work&#xff09;2.1 基于卡尔曼滤波器的多目标跟踪算法&#xff08;Multi-Object Tracking using Kalman Filter&#xff09;2.2 基于定位的多目标跟踪…
阅读更多...
Elasticsearch：Simulate ingest API

Elasticsearch：Simulate ingest API

Ingest pipeline 为我们摄入数据提供了极大的方便。在我之前的文章中&#xff0c;有非常多的有关 ingest pipeline 的文章。请详细阅读文章 “Elastic&#xff1a;开发者上手指南”。针对一组提供的文档执行摄取管道&#xff0c;可以选择使用替代管道定义。 Simulate ingest AP…
阅读更多...
如何查找SpringBoot应用中的请求路径（不使用idea）

如何查找SpringBoot应用中的请求路径（不使用idea）

背景 昨天有个同事向我咨询某个接口的物理表是哪个&#xff0c;由于公司业务较多、这块业务的确不是我负责的&#xff0c;也没有使用idea不能全局搜索(eclipse搜不到jar内的字符串)&#xff0c;也就回复了不清楚。 除了自己写代码输出servlet的路径和类外&#xff0c;发现了一…
阅读更多...
【C++】list容器功能模拟实现

【C++】list容器功能模拟实现

介绍 上一次介绍了list队容器的迭代器模拟&#xff0c;这次模拟实现list的简单功能&#xff0c;尤其要注意构造函数、析构函数、以及赋值运算符重载的实现。 list容器需要接纳所有类型的数据&#xff0c;因此&#xff0c;结构设置与迭代器设置同理&#xff0c;需要引入结点&…
阅读更多...
邮件服务支持Exchange协议，资产历史账号支持设置保留数量，JumpServer堡垒机v3.10.2 LTS版本发布

邮件服务支持Exchange协议，资产历史账号支持设置保留数量，JumpServer堡垒机v3.10.2 LTS版本发布

2024年1月22日&#xff0c;JumpServer开源堡垒机正式发布v3.10.2 LTS版本。JumpServer开源项目组将对v3.10 LTS版本提供长期的支持和维护&#xff0c;并定期迭代发布小版本。欢迎广大社区用户升级至v3.10 LTS版本&#xff0c;以获得更佳的使用体验。 在v3.10.2 LTS版本中&…
阅读更多...
LeetCode203 移除链表元素

LeetCode203 移除链表元素

203. 移除链表元素 给你一个链表的头节点 head 和一个整数 val &#xff0c;请你删除链表中所有满足 Node.val val 的节点&#xff0c;并返回 新的头节点 。 示例 1&#xff1a; 输入&#xff1a;head [1,2,6,3,4,5,6], val 6 输出&#xff1a;[1,2,3,4,5] 示例 2&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023