王有志，一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群：共同富裕的Java人

上一篇我们学习了平衡二分搜索树的理论知识，并学习了AVL树是如何保持二分搜索树的平衡的，今天我们一起来实现AVL树。
Tips：

• AVL树和数据结构：二分搜索树中的二分搜索树非常相似；
• 分别使用Java和Python实现AVL树，Python版本仅供大家批评。

记录节点高度

首先对二分搜索树的节点进行改造，使它可以记录自身的高度：

public class TreeNode<E extends Comparable<E>> {
	private E element;
	private TreeNode<E> left;
	private TreeNode<E> right;
	private int height;
	public TreeNode(E element) {
		this.element = element;
		this.height = 1;
	}
}

Python版本：

class TreeNode(object):
	def __init__(self, element, left=None, right=None):
		self.element = element
		self.left = left
		self.right = right
		self.height = 1

接着在AVL树中提供辅助函数，用来获取节点的高度，要针对null（None）的情况进行处理：

public class AVLTree<E extends Comparable<E>> extends BinarySearchTree<E> {
	private int getHeight(TreeNode<E> node) {
		return node == null ? 0 : node.getHeight();
	}
}

Python版本：

class AVLTree(object):
	def __init__(self):
		self.root = None
	def getHeight(self, node):
		if node is None:
			return 0
		else:
			return node.height

Tips：为了简便Python版本中的element为数字类型。

计算平衡因子

记录高度之后，就可以计算节点的平衡因子了，而AVL树正是根据平衡因子来决定是否通过旋转来维持平衡。
添加获取平衡因子的辅助函数，逻辑非常简单，计算左右子树高度差即可：

private int getBalanceFactor(TreeNode<E> node) {
	if(node == null) {
		return 0;
	}
	return getHeight(node.getLeft()) - getHeight(node.getRight());
}

Python版本：

def _getBalanceFactor(self, node):
	if node is None:
		return 0
	return self._getHeight(node.left) - self._getHeight(node.right)

好了，到目前为止，准备工作已经差不多了，接下来我们要开始修改改变树结构的的添加方法。
Tips：

• 可以利用二分搜索树和平衡二分搜索树的特性，添加检查是否为平衡二分搜索树的辅助功能；
• 删除方法的原理相同，文章中不再展示代码展示，可以查看后文的代码仓库。

修改添加方法

AVL树中节点的高度并不是一成不变的，它会随着结构的变化而变化，当添加或者删除节点后，树的结构都会发生变化。
当结构发生变化时，我们需要维护节点的高度，并计算平衡因子，以决定是否需要进行旋转维持平衡。递归的实现中维护节点的高度非常容易，只需要获取左右子树的最大高度后加1即可，而计算平衡因子可以通过之前的辅助函数完成：

@Override  
public void add(E element) {
	this.root = add(this.root, element);
}

private TreeNode<E> add(TreeNode<E> node, E element) {
	if (node == null) {
		this.size++;
		return new TreeNode<>(element);
	}
	if (element.compareTo(node.getElement()) > 0) {
		node.setRight(add(node.getRight(), element));
	} else {
		node.setLeft(add(node.getLeft(), element));
	}

	// 上面的逻辑和二分搜索树相同
	// 维护当前节点的高度
	node.setHeight(Math.max(getHeight(node.getRight()), getHeight(node.getLeft())) + 1);
	// 计算平衡因子
	int balanceFactor = getBalanceFactor(node);
}

Python版本：

def add(self, element):
	self.root = self._add(self.root, element)
def _add(self, node, element):
	if node is None:
		self.size = self.size + 1
		return TreeNode(element)
	if element > node.elment:
		node.right = self._add(node.right, element)
	else:
		node.left = self._add(node.left, element)

	# 维护当前节点的高度
	node.height = max(self._getHeight(node.right), self._getHeight(node.left)) + 1
	# 计算平衡因子
	balanceFactor = self._getBalanceFactor(node)

旋转维护平衡

当不平衡发生时，即balanceFactor > 1，可能存在多种情况：

• 当左子节点的平衡因子大于0，可以通过右旋转恢复平衡；
• 当右子节点的平衡因子大于0，可以通过左旋转恢复平衡。

Tips：

• 如果忘记了树旋转的原理可以回顾下数据结构：平衡二分搜索树；
• 这里将恢复LL失衡的LL旋转称为右旋转。

单旋（LL旋转）

为了方便理解，我们把数据结构：平衡二分搜索树的LL旋转图示拿过来。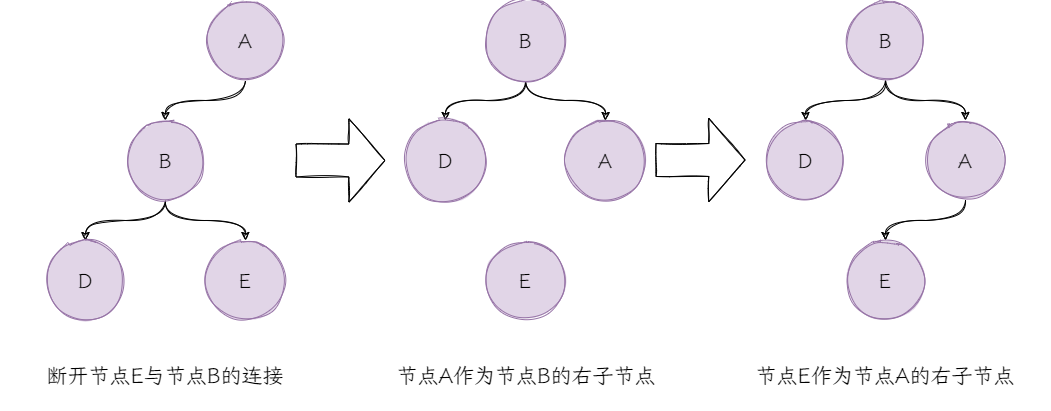

来看图翻译代码：

private TreeNode<E> rightRotate(TreeNode<E> node) {

	// 暂存节点B
	TreeNode<E> leftChild = node.getLeft();

	// 暂存节点E，A的左孩子的右孩子
	TreeNode<E> leftChildRightChild = leftChild.getRight();

	// 右旋转
	// 节点A作为节点B的右孩子
	leftChild.setRight(node);

	// 节点E作为节点A的左孩子
	node.setLeft(leftChildRightChild);

	// 更新节点的Height，只有节点A和节点B的高度发生了变化
	node.setHeight(Math.max(getHeight(node.getRight()), getHeight(node.getLeft())+ 1));
	leftChild.setHeight(Math.max(getHeight(leftChild.getRight()), getHeight(leftChild.getLeft())+ 1));


	// 返回节点B，新的根节点
	return leftChild;
}

Python版本：

def _rightRotate(self, node):
	leftChild = node.left
	leftChildRightChild = leftChild.getRight
	leftChild.right = node
	node.left = leftChildRightChild
	node.height = max(self._getHeight(node.right), self._getHeight(node.left)) + 1
	leftChild.height = max(self._getHeight(leftChild.right), self._getHeight(leftChild.left)) + 1
	return leftChild

看图翻译代码是不是简单很多？这也就是我为什么会在和王有志一起学习数据结构和算法中建议大家画数据结构。

双旋（LR旋转）

回顾下上一篇文章，在应对LR失衡的场景中，我们先对R失衡的部分进行RR旋转，使整体称为LL失衡，接着进行LL旋转恢复平衡。那么代码是不是就非常容易了？

node.setLeft(leftRotate(node.getLeft()));
return rightRotate(node);

Python版本：

node.left = self._leftRotate(node.left)
return self._rightRotate(node)

是不是想复杂了？以为我们要写leftRightRotate方法？其实我们结合一下就可以完成看似复杂的LR旋转或者RL旋转。

完善添加方法

回顾头来看add方法，目前我们还剩最后一个疑问，如何判断产生了哪种失衡场景？
我们先来看“左重右轻”的场景，即LL失衡和LR失衡。此时一定有getBalanceFactor(node) > 1，即左边高于右边。那么它们的差别就在于node.getLeft()了。在LL失衡的场景中，一定有getBalanceFactor(node.getLeft()) >= 0，而在LR失衡的场景中，则是getBalanceFactor(node.getLeft()) < 0。
至于“右重左轻”的场景，只需要反过来即可。那么我们在添加方法计算balanceFactor后添加如下旋转场景：

// LL失衡
if(balanceFactor > 1 && getBalanceFactor(node.getLeft()) >= 0) {
	return rightRotate(node);  
}

// RR失衡
if(balanceFactor < -1 && getBalanceFactor(node.getRight()) <= 0) {
	return leftRotate(node);  
}

// LR失衡
if(balanceFactor > 1 && getBalanceFactor(node.getLeft()) < 0) {
	node.setLeft(leftRotate(node.getLeft()));
	return rightRotate(node);  
}

// RL失衡
if(balanceFactor < -1 && getBalanceFactor(node.getRight()) > 0) {
	node.setRight(rightRotate(node.getRight()));
	return leftRotate(node);
}

Python版本：

# RR失衡
if balanceFactor > 1 and self._getBalanceFactor(node.left) >= 0:
	return self._rightRotate(node)

# LR失衡
if balanceFactor < -1 and self._getBalanceFactor(node.right) <= 0:
	return self._leftRotate(node)

# LR失衡
if balanceFactor > 1 and self._getBalanceFactor(node.left) < 0:
	node.left = self._leftRotate(node.left)
	return self._rightRotate(node)

# RL失衡
if balanceFactor < -1 and self._getBalanceFactor(node.right) > 0:
	node.right = self._rightRotate(node.right)
	return self._leftRotate(node)

结语

今天的内容还是比较简单的，类似于小学的看图写作，只不过我们这次是将图示的过程翻译成的代码。
大家可以重点理解下各种旋转的过程（实际上还是上一篇的内容），至于叫法，大家就不用太纠结。
下一篇呢，会和大家分享另一棵平衡二分搜索树–大名鼎鼎的红黑树。

练习

• 实现AVL树的leftRotate方法
• 实现AVL树的删除方法
• 比较AVL树二分搜索树在性能上的提升

---

如果本文对你有帮助的话，还请多多点赞支持。如果文章中出现任何错误，还请批评指正。最后欢迎大家关注分享硬核Java技术的金融摸鱼侠王有志，我们下次再见！