目录
1 什么是回归分析
1.1 什么是线性回归
1.2非线性回归
2 数据和判断方法
2.1 原始数据
2.2 判断方法:最小二乘法
3 关于线性回归的实测
3.1 用直线模拟
3.2 怎么判断哪个线性模拟拟合更好呢?
3.2.1 判断标准
3.2.2 最小二乘法
3.2.3 高维度数据
3.3 用python来算下?(暂缺,用plot画图?)
4 关于误差和 E(θ)=1/2*(f(xi)-yi)^2 这个函数本身
4.0 注意新手错误
4.1 E(θ)这个函数本身
4.2 E(θ) 是否有最小值?
4.3 但是如何获得这个最小值呢?
4.3.1 方法1,直接求导数
4.3.2 如果找到E(θ)的最小值,就能找到对应的参数
5 用最速下降方法找到一个函数的最小值
5.1 最速下降法
5.2 假设 f(x) 如下,且从图像上看是有最小值的
5.3 最速下降方法的详细计算过程
5.3.0 最速下降方法公式
5.3.2 先分析函数f(x) 和其导函数 f(x)'
5.3.3 最速下降方法的迭代过程
5.3.4 可以看到2个结论
1 什么是回归分析
- 从时序数据来看,从过去数据去分析,生成1个模拟曲线。
- 然后用这个模拟曲线去,用新的 x 去预测新的数据
1.1 什么是线性回归
- 线性,就是指直线
- 从线性代数的角度来看,就是这些向量是否线性相关,如果线性无关就是共线。
- 线性回归,就是回归分析的模拟曲线是直线
1.2非线性回归
- 如果用曲线模拟,也就是用非一次函数/非直线去模拟
- 这样就是非线性回归了把
- 等会儿试试
2 数据和判断方法
2.1 原始数据
- 构造的原始数据
- 故意构造了一个类二维曲线数据,这样用直线去模拟就一定有较大的误差
- ROUND(0.5*C10^1.8+0.5*C10+2,0)


2.2 判断方法:最小二乘法
- 均方误差 MSE=1/n*(f(xi)-yi)^2
- 误差和:E(θ)1/2*(f(xi)-yi)^2 ,类似MSE
3 关于线性回归的实测
3.1 用直线模拟
做了3个线性模拟
- f(x)=1+2x
- f(x)=1+3x
- f(x)=1+2.8x
3.2 怎么判断哪个线性模拟拟合更好呢?
3.2.1 判断标准
- E(θ)=1/2*(f(xi)-yi)^2
- 判断标准就是用 E(θ),哪个E(θ)更小,哪个的拟合效果更好。
- 配合图形上曲线的对比,也可以看到这个结论
3.2.2 最小二乘法
- 用E(θ)的大小可以判断不同的拟合曲线的优劣
- 理论上E(θ)趋近于0,就可以找出拟合最好的曲线
3.2.3 高维度数据
实际上即使不是二维数据,不能用图形化的形式直观的看到。
仍然还是可以用E(θ)=1/2*(f(xi)-yi)^2来判断,比较,模拟曲线的拟合程度
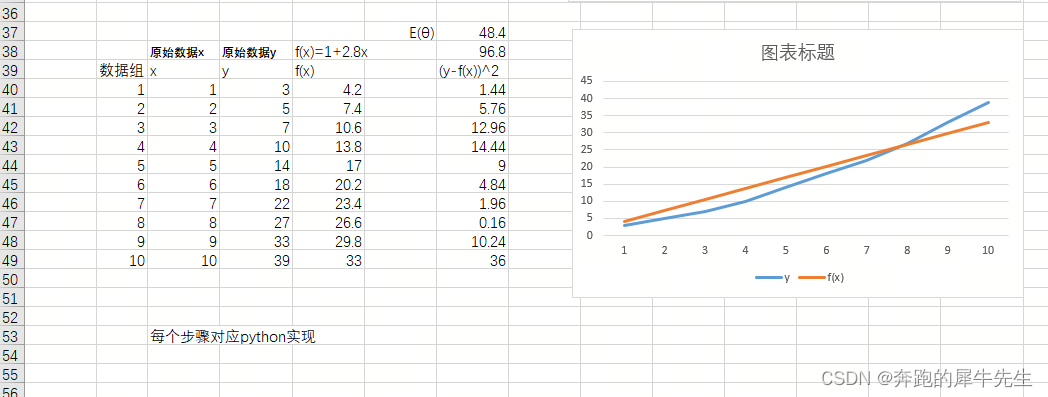
- 上帝视角的 y=ROUND(0.5*C10^1.8+0.5*C10+2,0)
- f(x)=1+2x , E(θ)=352
- f(x)=1+3x, E(θ)=60.5
- f(x)=1+2.8x,E(θ)=48.4
- 从图形看,f(x)=1+2.8x , E(θ)=48.4 ,这个直线模拟的效果也确实相对更好

3.3 用python来算下?(暂缺,用plot画图?)
4 关于误差和 E(θ)=1/2*(f(xi)-yi)^2 这个函数本身
4.0 注意新手错误
- 要分析得是 E(θ) 是否有最小值,从而找到误差最小得模拟曲线--以及模拟曲线的参数。
- 而不是分析f(x) 这个模拟函数是否有最小值!!
4.1 E(θ)这个函数本身
- 一般来说是多元函数曲线
- 这样很可能就有最小值

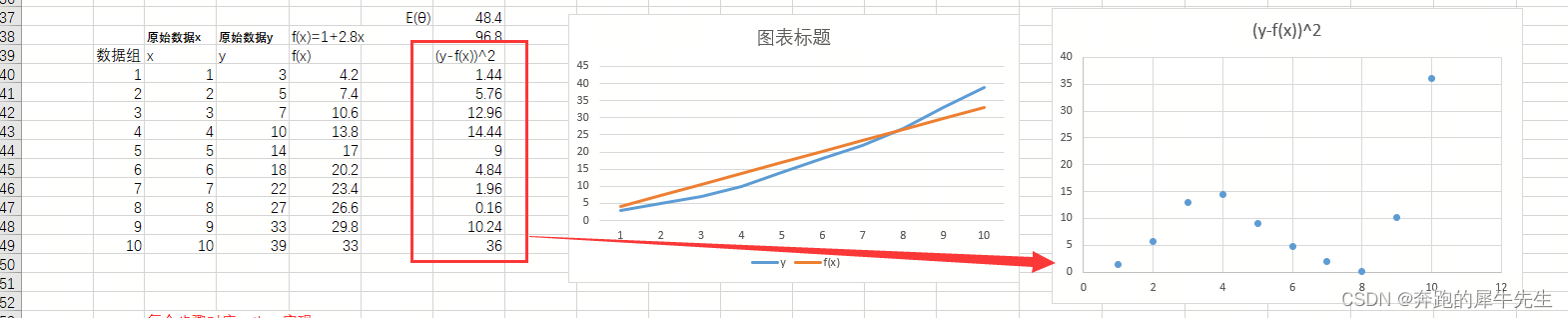
4.2 E(θ) 是否有最小值?
- 首先说明
- 如果E(θ)=1/2*(f(xi)-yi)^2 这个函数本身 是直线,哪是无法找到最小值的
- 如果E(θ)是一个开头向下,向上凹的曲线,也是没有最小值的
- 只有E(θ)是一个开头向上,向下凹的曲线,即使有多个波段,也应该是有最小值的
例子:如果E(θ)=1/2*(f(xi)-yi)^2 这个函数本身 是直线,哪是无法找到最小值的

4.3 但是如何获得这个最小值呢?
- 方法1,直接求导数
- 方法2,用最速下降法来逐步达到最小值
4.3.1 方法1,直接求导数
- 知道函数形式后,求导函数
- 但是后面的函数可能很复杂,导函数不好求

4.3.2 如果找到E(θ)的最小值,就能找到对应的参数
- 后面说明怎么求这样E(θ)函数的最小值
- 只有E(θ)是一个开头向上,向下凹的曲线,即使有多个波段,也应该是有最小值的
- 求E(θ)的最小值的目的,就是为了判断这个模拟曲线的拟合程度最好
- 而前提是,曲线足够通用,
- 比如 E(θ)=θ0+θ1x+θ2x^2+....
- 函数是通用形式,哪剩下的就是去用 求E(θ)的最小值得过程,去找到合适得 参数(θ0,θ1,θ2...)
5 用最速下降方法找到一个函数的最小值
5.1 最速下降法
- 最速下降方法:x=x-rate*f(x)'
- 用学习率找到 f(x)取最小值时的x
- 学习率一般要取小点,比如0.1,0.01 等等
- 学习率太大可能无法收敛
- 学习率太小收敛速度会慢
5.2 假设 f(x) 如下,且从图像上看是有最小值的

5.3 最速下降方法的详细计算过程
5.3.0 最速下降方法公式
- 最速下降方法:x=x-rate*f(x)'
- 用学习率找到 f(x)取最小值时的x
5.3.2 先分析函数f(x) 和其导函数 f(x)'
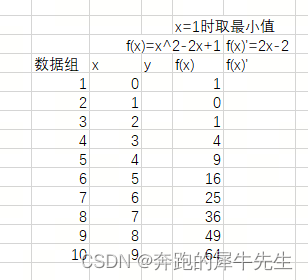
- x=1时取最小值
- 函数 f(x)=x^2-2x+1
- 导函数 f(x)'=2x-2 (那么x=1时,f(x)'=0就是f(x)取到最小值)
5.3.3 最速下降方法的迭代过程(不断迭代取新的x)
- 比如取 x=0为初始,rate=0.1
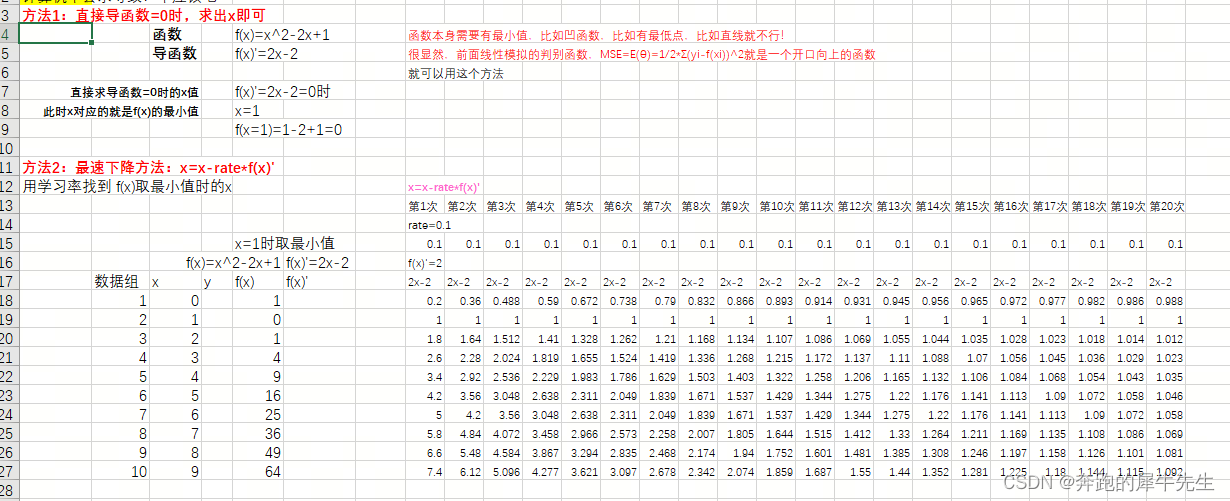
- 第1轮:new x= x-rate*f(x)' =0-0.1*(2*0-2)=0-0.1*(-2)=0.2,新增了0.2
- 第2轮:new x= x-rate*f(x)' =0.2-0.1*(2*0.2-2)=0.2-0.1*(-1.6)=0.2+0.16=0.36,新增了0.16
- 第2轮:new x= x-rate*f(x)' =0.36-0.1*(2*0.36-2)=0.36-0.1*(-1.28)=0.36+0.128=0.488,新增了0.128
5.3.4 可以看到几个结论
- 1)通过x=x-rate*f(x)' 公式迭代算出来的新的x, 每次增加的幅度再减小:0.2→0.16→0.128
- 2)只有增加值逐渐减小,这样计算多次后,x会收敛。
- 3)收敛在x=1与x的初始值无关,
- 可以看到无论x的初始值取多少,比如初始x=0 或者x=5,经过这个算法,计算20次后,都趋近了x=1这个值。
- 4)EXCEL里计算的数列是符合的,x=0时,这1行新x数据0.2 0.36 0.488 0.5904 0.67232 0.737856
5.3.5如果学习率rate=1 取值过大,导致永远无法收敛。见下图