目录
堆的定义:
堆的实现:
堆的元素插入:
堆元素删除:
堆初始化与销毁:
堆排序:
堆的定义:
堆是一种完全二叉树,完全二叉树定义如下:
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
堆分为两类:小堆和大堆。小堆是指堆中任意一个节点都值小于它的孩子节点值。同理,大推指任意一个节点的值都大于它孩子节点的值。
堆的结构:
事实上,堆在逻辑结构上可以看作是一种完全二叉树,但在内存中是以数组的方式存储的。堆内节点的下标可以在计算机内如此计算出来:
左孩子节点的下标 = 父节点的下标*2+1
右孩子节点的下标 = 父节点的下标*2+2
父节点的下标 = (子节点下标 - 1)/2

我们可以很容易看出来,堆数据的插入在逻辑上是一层一层地插入,这一层存满后再到下一层存储。
堆的实现:
Typedef 数据类型 DataType
struct heap {
DataType* t;//堆数组内数据类型,指向第一个元素的指针
int size; //堆内元素个数
int capacity; //堆内元素容量
}hp;堆的元素插入:
由于堆的结构特性,即小堆的双亲节点比它的子节点都要大,大堆的父节点比他的子节点都要小。因此每在数组后插入一个数据都要将这个数据调整到它应该存储的位置,这种调整在逻辑结构中是从下至上的顺序,因此也称为向上调整。
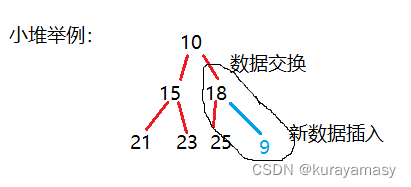
每次都与自己的双亲节点对比,在小堆中,如果双亲节点的数据大于插入的新数据,那么两节点作数据交换,依次作交换直到双亲节点数据小于该新插入的数据为止。
首先我们实现一个向上调整的代码:
void AdjustUp(HpType* a, int child)
{
int parent = (child - 1)/2;//先计算出当前插入数据节点的父节点下标
while(child > 0)
{
if(a[child] < a[parent])
{
HpType tmp = a[child];
a[child] = a[parent];
a[parent] = tmp; //交换两节点数据
parent = child;
child = (parent - 1)/2; //更新父子节点的值,使其指向下一组父子节点
}
else
{
break;
}
}
}实现完调整堆的代码后,我们可以实现插入数据:
void HeapPush(hp* php,HpDataType x)
{
assert(hp);
int newCapacity = php->Capacity == 0?4:2*Capacity;
HpDataType* tmp = (HpDataType*)realloc(php->a, newCapacity*sizeof(HpDataType);
if(tmp == null) //扩容失败的情况
{
perror("realloc failed");
}
php->t[php->size] = x;
php->size++;
AdjustUp(php->t,php->size - 1];//插入后调整堆
}堆元素删除:
堆元素删除是将堆首元素删除的算法。对于堆元素删除,通过上面的逻辑,像数组一样单纯将该数据从数组中移除并将后面的数据向前移动是不可行的,因为会导致堆结构的破坏,父节点和子节点不会形成一致的大小关系,因此我们要实现一个算法实现数据删除后对整个堆进行调整的。
堆元素删除的算法思想是,将堆末尾元素与首元素进行交换,并将末尾元素删除,此时要删除的元素已经被移出。然后将变换后堆的首元素进行向下调整,调整到它应在的位置。
void AdjustDown(HpDataType* a, int parent,int size)
{
int child = parent*2 + 1;
while(child < size)
{
if( child+1 < size && a[parent*2 + 1] > a[parent*2 + 2])
{
child++;
}
if(a[parent] > a[child])
{ swap(&a[parent],&a[child];
parent = child;
child = parent*2 + 1;
}
else
{
break;
}
}
}实现完向下调整算法后即可实现堆删除顶部元素算法:
void HeapPop(ph* php)
{
assert(php);
assert(!HeapEmpty(php));
swap(php->t[0],php->[size-1]); //将首尾元素进行交换
php->size--;
AdjustDown(ph,php->t[0],php->size); //向下调整元素
}堆初始化与销毁:
void HeapInit(hp* php)
{
assert(php);
php->t = null;
php->size = 0;
php->Capacity = 0;
}
void HeapDestroy(hp* php)
{
assert(php);
free(php);
}堆排序:
堆排序是很重要的一种排序,从堆的增删查改操作衍生而来,由于其较低的时间复杂度运用较为广泛。
堆排序算法运用到堆的向下调整和,首先传入一个未排序的数组,此时对该数组进行建堆操作。如果我们新建一个堆,再把数组内数据传入堆内会浪费较大的空间。有没有方法可以对数组本身进行建堆操作呢?
我们可以想象,对数组本身进行建堆操作,把数组看作是从第一个数开始一直插入n - 1个数形成。那么我们就可以将后面n - 1个数进行插入然后向上调整建堆。
void HeapSort(int* a,n)
{
for(int i = 1;i < n;i++)
{ AdjustUp(a,i);
}
}