文章目录
- 正则化
- 欠拟合和过拟合
- 正则化参数
正则化
机器学习中的正则化是在损失函数里面加惩罚项,增加建模的模糊性,从而把捕捉到的趋势从局部细微趋势,调整到整体大概趋势。虽然一定程度上地放宽了建模要求,但是能有效防止过拟合的问题,增加模型准确性。它影响的是模型的权重。
normalization 和 standardization :标准化、规范化,以及归一化,是调整数据,特征缩放;
regularization:而正则化,是调整模型,约束权重。
欠拟合和过拟合
正则化技术所要解决的过拟合问题,连同欠拟合(underfit)一起,都是机器学习模型调优(找最佳模型)、参数调试(找模型中的最佳参数)过程中的主要阻碍。
下面用图来描述欠拟合和过拟合。这是针对一个回归问题的3个机器学习模型,如下图所示。
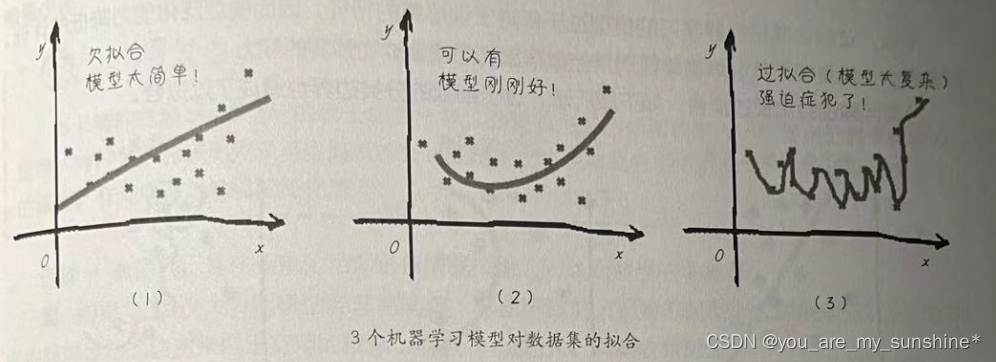
发现上图第1个简单的函数模型不如复杂一点的模型拟合效果好,所以调整模型之后,有可能会得到更小的均方误差(上图第2个)。如果继续追求更完美的效果,甚至接近于0的损失,可能会得到类似于上图第3个函数图形。
不能主要看训练集上的损失,更重要的是看测试集上的损失。让我们画出机器学习模型优化过程中的误差图像,如下图所示。
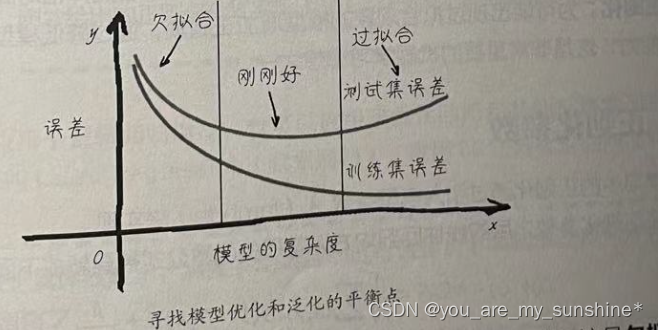
看得出来,一开始模型“很烂”的时候,训练集和测试集的误差都很大,这是欠拟合。随着模型的优化,训练集和测试集的误差都有所下降,其中训练集的误差值要比测试集的低。这很好理解,因为函数是根据训练集拟合的,泛化到测试集之后表现会稍弱一点。但是,如果此处继续增加模型对训练集的拟合程度,会发现测试集的误差将逐渐升高。这个过程就被称作过拟合。
模型的复杂度可以代表迭代次数的增加(内部参数的优化),也可以代表模型的优化(特征数量的增多、函数复杂度的提高,比如从线性函数到二次、多次函数,或者说决策树的深度增加,等等)。
所以,过拟合就是机器学习的模型过于依附于训练集的特征,因而模型泛化能力降低的体现。泛化能力,就是模型从训练集移植到其他数据集仍然能够成功预测的能力。
分类问题也会出现过拟合,如下图所示,过于细致的分类边界也造成了过拟合。
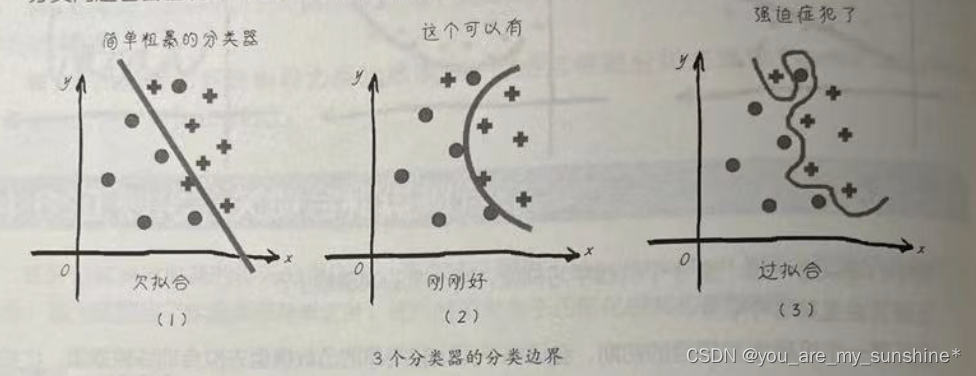
过拟合现象是机器学习过程中怎么甩都甩不掉的阴影,影响着模型的泛化功能,因此我们几乎在每一次机器学习实战中都要和它作战!
刚才用逻辑回归模型进行心脏病预测的时候,我们也遇见了过拟合问题。那么,有什么方法解决吗?
降低过拟合现象通常有以下几种方法。
- 增加数据集的数据个数。数据量太小时,非常容易过拟合,因为小数据集很容易精确拟合。
- 找到模型优化时的平衡点,比如,选择迭代次数,或者选择相对简单的模型。
- 正则化。为可能出现过拟合现象的模型增加正则项,通过降低模型在训练集上的精度来提高其泛化能力,这是非常重要的机器学习思想之一。
正则化参数
机器学习中的正则化通过引入模型参数λ(lambda)来实现。
加入了正则化参数之后的线性回归均方误差损失函数公式被更新成下面这样:
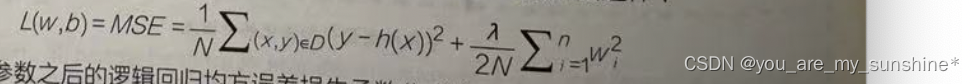
加入了正则化参数之后的逻辑回归均方误差损失函数公式被更新成下面这样:

现在的训练优化算法是一个由两项内容组成的函数:一个是损失项,用于衡量模型与数据的拟合度;另一个是正则化项,用于调解模型的复杂度。
从直观上不难看出,将正则化机制引入损失函数之后,当权重大的时候,损失被加大,λ值越大,惩罚越大。这个公式引导着机器在进行拟合的时候不会随便增加权重。
正则化的目的是帮助我们减少过拟合的现象,而它的本质是约束(限制)要优化的参数。
正则化的本质,就是崇尚简单化。同时以最小化损失和复杂度为目标,这称为结构风险最小化。
选择λ值的目标是在简单化和训练集数据拟合之间达到适当的平衡。
- 如果λ值过大,则模型会非常简单,将面临数据欠拟合的风险。此时模型无法从训练数据中获得足够的信息来做出有用的预测。而且λ值越大,机器收敛越慢。
- 如果λ值过小,则模型会比较复杂,将面临数据过拟合的风险。此时模型由于获得了过多训练数据特点方面的信息而无法泛化到新数据。
- 将λ设为0可彻底取消正则化。在这种情况下,训练的唯一目的是最小化损失,此时过拟合的风险较高。
正则化参数通常有L1正则化和L2正则化两种选择。
- L1正则化,根据权重的绝对值的总和来惩罚权重。在依赖稀疏特征(后面会讲什么是稀疏特征)的模型中,L1正则化有助于使不相关或几乎不相关的特征的权重正好为0,从而将这些特征从模型中移除。
- L2正则化,根据权重的平方和来惩罚权重。L2正则化有助于使离群值(具有较大正值或较小负值)的权重接近于0,但又不会正好为0。在线性模型中,L2正则化比较常用,而且在任何情况下都能够起到增强泛化能力的目的。
刚才给出的正则化公式实际上是L2正则化,因为权重w正则化时做了平方。
正则化不仅可以应用于逻辑回归模型,也可以应用于线性回归和其他机器学习模型,应用L1正则化的回归又叫 Lasso Regression(套索回归),应用L2正则化的回归又叫Ridge Regression(岭回归)。
而最佳λ值则取决于具体数据集,需要手动或自动进行调整。
学习机器学习的参考资料:
(1)书籍
利用Python进行数据分析
西瓜书
百面机器学习
机器学习实战
阿里云天池大赛赛题解析(机器学习篇)
白话机器学习中的数学
零基础学机器学习
图解机器学习算法
…
(2)机构
光环大数据
开课吧
极客时间
七月在线
深度之眼
贪心学院
拉勾教育
博学谷
…