目录
一、冒泡排序
1、冒泡排序思想
2、冒泡排序算法的性能分析
代码实现:
二、选择排序
1、选择排序思想
2、选择排序算法的性能分析
代码实现:
一、冒泡排序
1、冒泡排序思想
冒泡排序的基本思想是通过相邻元素之间的比较和交换来逐步将最大(或最小)的元素移到右边(或左边)。具体来说,冒泡排序的步骤如下:
- 从数组的第一个元素开始,依次比较相邻的两个元素。如果前面的元素大于后面的元素,则交换它们的位置,以使较大的元素向右移动。
- 继续向数组的下一个相邻元素进行比较和交换,直到最后一个元素,此时最大的元素已经移到了数组的最右侧。
- 重复以上步骤,但这次只需要比较和交换前 n-1 个元素,因为最大的元素已经在正确的位置上。
- 重复进行 n-1 轮比较和交换,直到所有元素都按照从小到大(或从大到小)的顺序排列。
2、冒泡排序算法的性能分析
- 最好的情况下,当输入数组已经是有序的,冒泡排序只需进行一轮比较,时间复杂度为 O(n)。
- 最坏的情况下,当输入数组是逆序的,冒泡排序需要进行 n-1 轮比较和交换,时间复杂度为 O(n^2)。
- 平均情况下,冒泡排序的时间复杂度为 O(n^2)。
- 冒泡排序是一种稳定排序算法,不会改变相等元素的相对顺序。
- 冒泡排序是一种原地排序算法,不需要额外的空间。
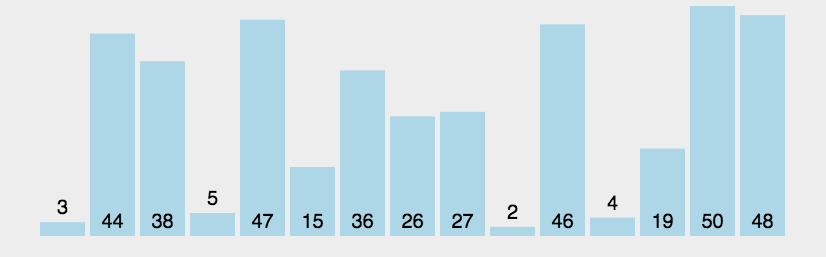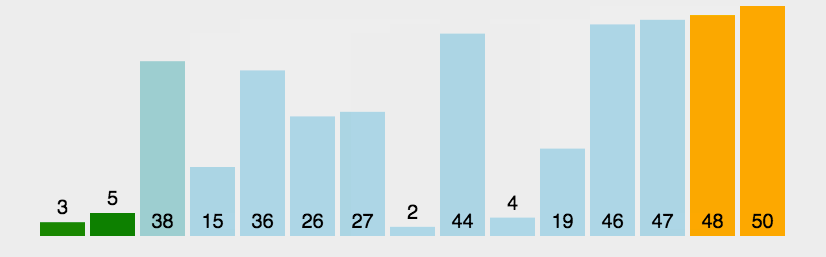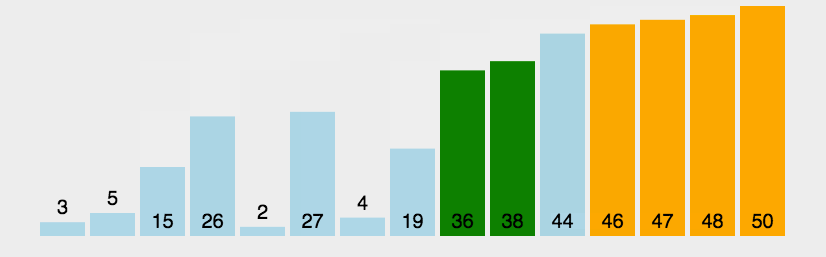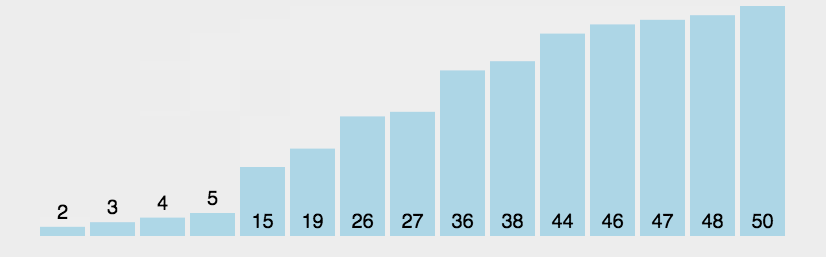
代码实现:
1、普通版本:
// 定义一个交换函数,用于交换两个整数的值
void swap(int* a, int* b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
// 冒泡排序函数,对数组进行排序
void BubbleSort(int* a, int n)
{
int i, j;
// 外层循环控制排序的轮数
for (i = 0; i < n - 1; i++)
{
// 内层循环进行相邻元素的比较和交换
for (j = 0; j < n - i - 1; j++)
{
// 如果前一个元素大于后一个元素,则交换它们的位置
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
}
}
}
}2、优化版本 :
思想:在优化版本的冒泡排序算法中,通过添加一个标记变量flag,可以在一轮排序过程中标记是否有进行过交换操作,如果某一轮排序中没有进行过任何交换,说明数组已经有序,可以提前结束排序。
// 定义一个交换函数,用于交换两个整数的值
void swap(int* a, int* b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}
// 冒泡排序函数,对数组进行排序
void BubbleSortPro(int* a, int n)
{
int i, j, flag = 0;
// flag用于标记是否有交换发生,初始值为0
// 外层循环控制排序的轮数
for (i = 0; i < n - 1; i++)
{
flag = 0; // 在每一轮开始时,将flag重置为0
// 内层循环进行相邻元素的比较和交换
for (j = 0; j < n - i - 1; j++)
{
// 如果前一个元素大于后一个元素,则交换它们的位置,并将flag设置为1
if (a[j] > a[j + 1])
{
swap(&a[j], &a[j + 1]);
flag = 1;
}
}
// 如果在一轮排序中没有进行过任何交换,说明数组已经有序,可以提前结束排序
if (flag == 0)
{
break;
}
}
}二、选择排序
1、选择排序思想
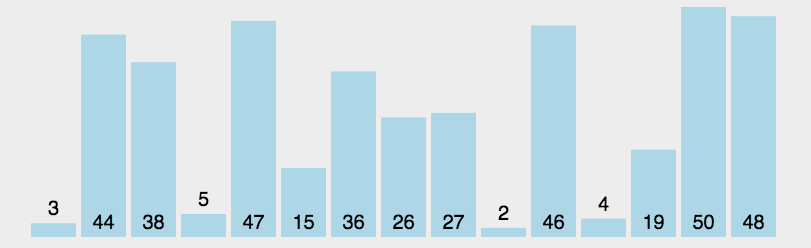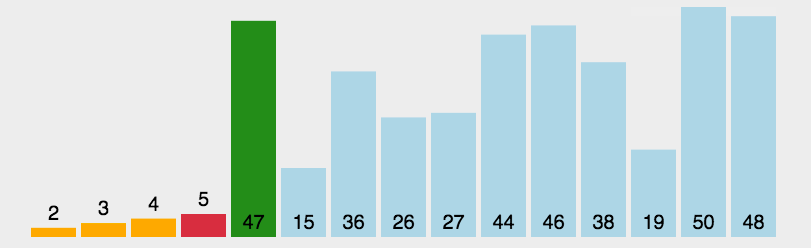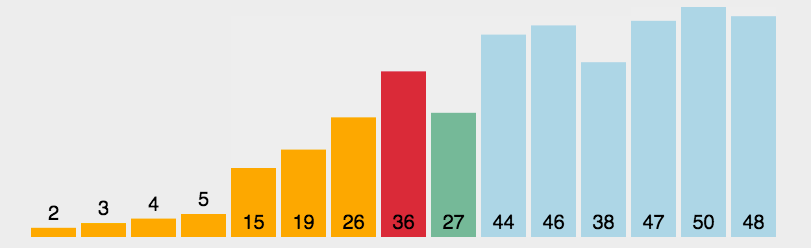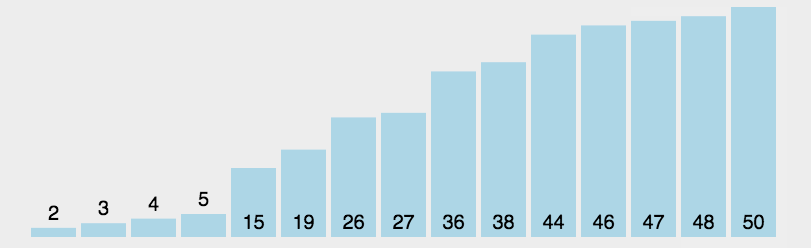
选择排序的基本思想可以概括为以下几个步骤:
- 遍历待排序的数组,将数组中的第一个元素视为当前最小值。
- 在剩余的未排序部分中,依次查找比当前最小值更小的元素。
- 如果找到了比当前最小值更小的元素,则将其标记为新的最小值。
- 遍历完未排序部分,将新的最小值与当前最小值交换位置。
- 如此循环,直到所有元素都被排序。
通过每次从剩余未排序部分选择最小的元素,并将其放在已排序部分的末尾,逐步构建有序序列。
2、选择排序算法的性能分析
- 选择排序的时间复杂度为O(n^2),其中n是待排序数组的元素个数。这是因为在每一轮遍历中,需要比较剩余未排序部分的所有元素,最坏情况下要进行n-1次比较。总共需要进行n-1轮遍历,因此时间复杂度为O(n^2)。
- 选择排序是一种不稳定的排序算法。当待排序数组中存在相同元素时,选择排序可能会改变相同元素的相对顺序。具体来说,在选择过程中,如果当前的最小元素与其他相同元素交换位置,可能会改变它们的相对顺序。
- 选择排序是一种原地排序算法,即排序过程中不需要额外的空间。它只需要一个额外的变量来记录最小(或最大)元素的位置,通过交换元素位置来实现排序,所以空间复杂度为O(1)。
综上所述,选择排序的时间复杂度为O(n^2),空间复杂度为O(1),并且是一种不稳定的排序算法。
代码实现:
1、普通版本:
void swap(int* a,int* b)
{
int temp;
temp=*a;
*a=*b;
*b=temp;
}
void SelctSort(int* a, int n)
{
int i, j, key;
// 遍历数组,i表示已排序部分的末尾元素的索引
for (i = 0; i < n - 1; i++)
{
key = i; // 将当前位置视为最小值的索引
// 在未排序部分中查找最小值
for (j = i + 1; j < n; j++)
{
if (a[key] > a[j])
{
key = j; // 更新最小值的索引
}
}
// 如果最小值不是当前位置的元素,则交换位置
if (key != i)
{
swap(&a[i], &a[key]);
}
}
}2、优化版本
优化版本的思想是在选择排序的基础上,同时追踪并找出未排序部分的最大值和最小值,并将它们分别放置在已排序部分的末尾和开头。通过这种方式,可以减少交换的次数,从而提高排序的效率。
void swap(int* a,int* b)
{
int temp;
temp=*a;
*a=*b;
*b=temp;
}
void SelctSortPro(int* a, int n)
{
int i, j;
int begin = 0, end = n - 1;
int maxi = end, mini = begin;
// 在每一次循环中,将未排序部分的最大值和最小值分别放置在已排序部分的末尾和开头
while (begin < end)
{
i = begin;
j = end;
maxi = end;
mini = begin;
// 在未排序部分中查找最大值和最小值
while (i <= end)
{
if (a[maxi] < a[i])
{
maxi = i; // 更新最大值的索引
}
if (a[mini] > a[i])
{
mini = i; // 更新最小值的索引
}
i++;
}
// 将最小值放置在已排序部分的开头
swap(&a[begin], &a[mini]);
// 如果最大值所在位置等于begin,更新最大值所在位置为mini
if (maxi == begin)
{
maxi = mini;
}
// 将最大值放置在已排序部分的末尾
swap(&a[end], &a[maxi]);
// 更新已排序部分和未排序部分的起始和结束位置
begin++;
end--;
}
}