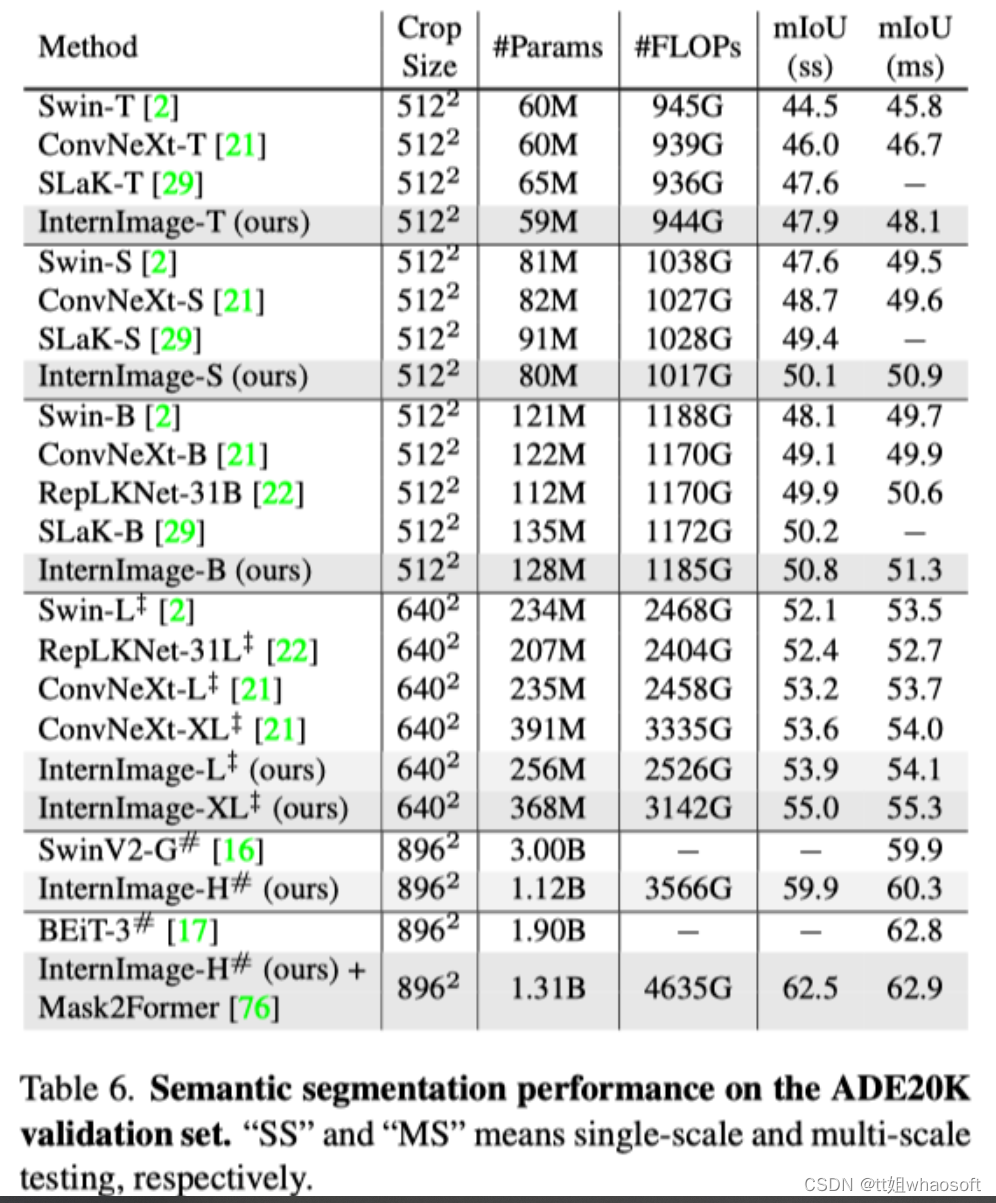
论文地址:基于低秩分解的网络异常检测综述
摘要:
异常检测对于网络管理与安全至关重要.国内外大量研究提出了一系列网络异常检测方法,其 中大多数方法更关注数据包及其独立时序数据流的分析、检测与告警,这类方法仅仅利用了网络数据之 间的时间相关性,无法检测新类型的网络异常,且难以定位以及剔除异常数据.为了解决上述问题,相关 研究融合多时间序列数据流,提出基于低秩分解的网络异常检测方法.该方法充分利用网络数据之间的 时间 空间相关性,无监督地定位异常数据所在位置,同时将异常数据剔除,从而还原网络正常数据.首 先,根据其对正常数据与异常数据的不同类型约束,将基于低秩分解的异常检测方法分为4类,并介绍 每一类方法的基本思想和优缺点;然后,探讨现有基于低秩分解的异常检测方法存在的挑战;最后,对未 来可能的发展趋势进行了展望.
研究背景
单点异常
单点异常即与全局数据的行为模型不同的单点数据.异常数据在数据集中单个出现,不产生聚集.例如某一局域网中,存在某一网络节点发生拥塞,导致其丢包率远远高于其余网络节点,那么该网络节点即为单点异常.单点异常作为最简单的一种异常种类,通常只需要简单的聚类、分类算法即可进行有效检测.网络中 U2R,R2L等攻击通常可视为单点异常.
集体异常
通常由多个对象组合构成,即单独观测某一 独立个体可能并不存在异常,但是这些个体同时出 现则构成一种异常.集体异常通常是由若干个单点组成,例如,拒绝服务攻击通常由攻击者控制大量傀 儡机向服务器发送请求来抢占服务器资源,使服务 器无法响应正常请求,达到攻击服务器的目的.
上下文异常
上下文异常通常被定义为:当数据点的值与同一上下文 环境中的其他数据点明显不同时,该数据点被认为是上下文异常值.值得注意的是,同一个值发生在不 同的上下文环境中,可能不会被认为是离群值.当我们讨论日志异常检测任务时,“上下文”通常表示为 日志文件所示上下文;而当我们讨论时间序列异常 检测任务时,“上下文”则表示时间.因此,在网络异 常检测中,日志异常、时序数据异常通常可视为上下 文异常.
传统异常检测方法
基于距离的方法:分析数据样本之间的距离,正常数据点与其近邻 数据相近,而异常数据点则更远。
基于密度的方法:分析数据样本空间的密度分度,邻域密度越低的 数据,越有可能是异常数据。
基于概率统计的方法:通过概率统计的方法,构建正常数据分布,属于正常数据分布的概率越小,越有可能是异常数据。
异常检测算法
数据挖掘/机器学习方法:关联分析、序列分析、聚类分析、决策树分析、贝叶斯网络、遗传算法、支持向量机、Markov模型。
深度学习方法卷积神 经 网 络、循环神经网络、 自动编码机、玻尔兹曼机、深度置信网络。
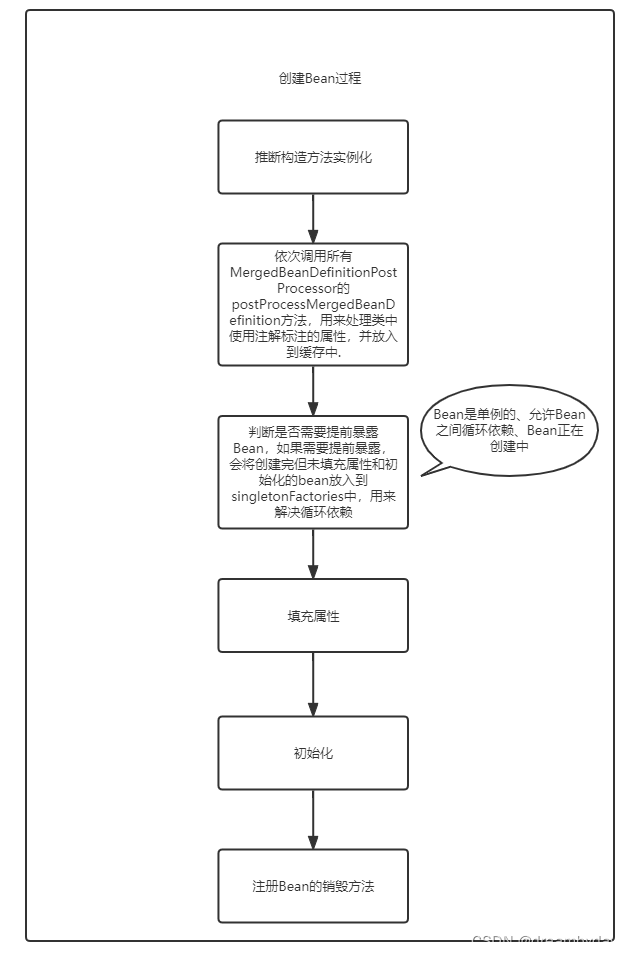
基于低秩分解的异常检测模型原理

通过分析图2(a)发现,网络性能数据在相邻时刻之间十分相似.图2(c)则显示相邻天之间的网络数据十分相似.因此,网络性能数据通常具有较强的时间稳定性,这就使得网络性能数据在时间维度(例 如图1中的时间)具有低秩性的特点.同样地,通过分析图2(b)发现不同 OD 对之间的网络数据向量具有较强的相关性,因此,网络数据同样具有较强的空间相关性,从而使得网络数据在空间维度(例如图1中的源节点目的节点对)具有低秩性的特点.
接下来我们使用数学来证明低秩性:为了进一步验证网络数据的低秩性,我们将网 络性能数据按照图1所示建模为矩阵X,并对X 进 行奇异值分解(singularvaluedecomposition,SVD), 得到[X]=UΣVT.其中,Σ 为对角矩阵,Σ=diag(σ1, σ2,σR ,0,0),该矩阵的对角线上元素通常为 从大到小排列的结果.那么,矩阵X 的秩则为矩阵Σ 中非零元素的个数.值得注意的是,在实际的应用中, 由于网络的监测数据为连续数据存在一定的测量噪 音,因此,监测数据通常并不满足严格意义的低秩.根 据主成分分析算法的定义,奇异值越大,其所代表的 主成分越重要,其前k 个奇异值所占比重几乎等于 所有奇异值之和时,则可以认为这个矩阵为近似低 秩矩阵,并满足低秩性的特点.因此,通常利用指标来判断是否为近似低秩矩阵.

如图4所示,矩阵 X 为网络监测数据矩阵,利用低秩分解技术可以将其分解为正常数据矩阵 M 与异常数据矩阵E.正常数据具有低秩性的特点,网络攻击代价高的问题以及网络设备故障的稀疏性问题使得异常数据通常具有稀疏性的特点.因此,异常数据矩阵E通常为稀疏矩阵, 通过基于低秩分解的数据分离模型获得稀疏异常数据矩阵E后,即可对网络数据中是否存在异常进行判定,同时根据矩阵中非零元素所处位置可进行异常定位.
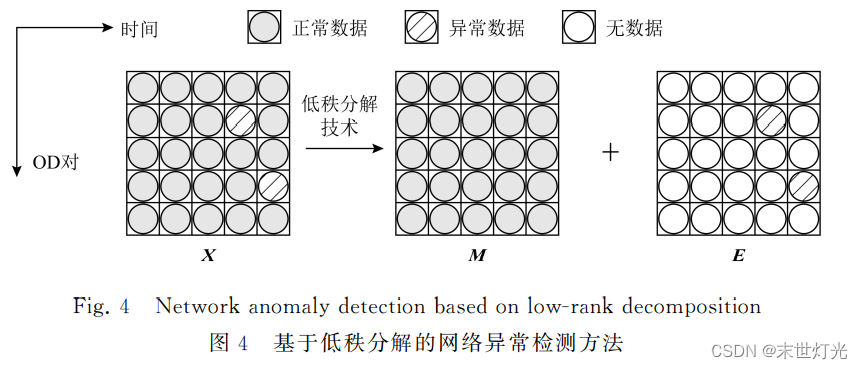
基于矩阵模型的异常检测方法

基于张量模型的异常检测方法
张量模型作为矩阵模型向多维的扩展,可以表征多模式数据的多维本质,张量模型不再局限于数据内比较简单的2维线性关系,而是将多维放到一起综合考虑,探索多因子、多成分、多线性关系,具有重要的学术价值和应用前景.


方法比较