| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
| 解题思路 |
|---|
- 已知矩阵相对有序,可以用二分搜索,不过和一维数组排序不同,这是二维的
- 每一行都递增,每一列也是递增,所以每一行的最后一个元素都是当前行最大的。每一列的最下面元素也都是当前列最大的
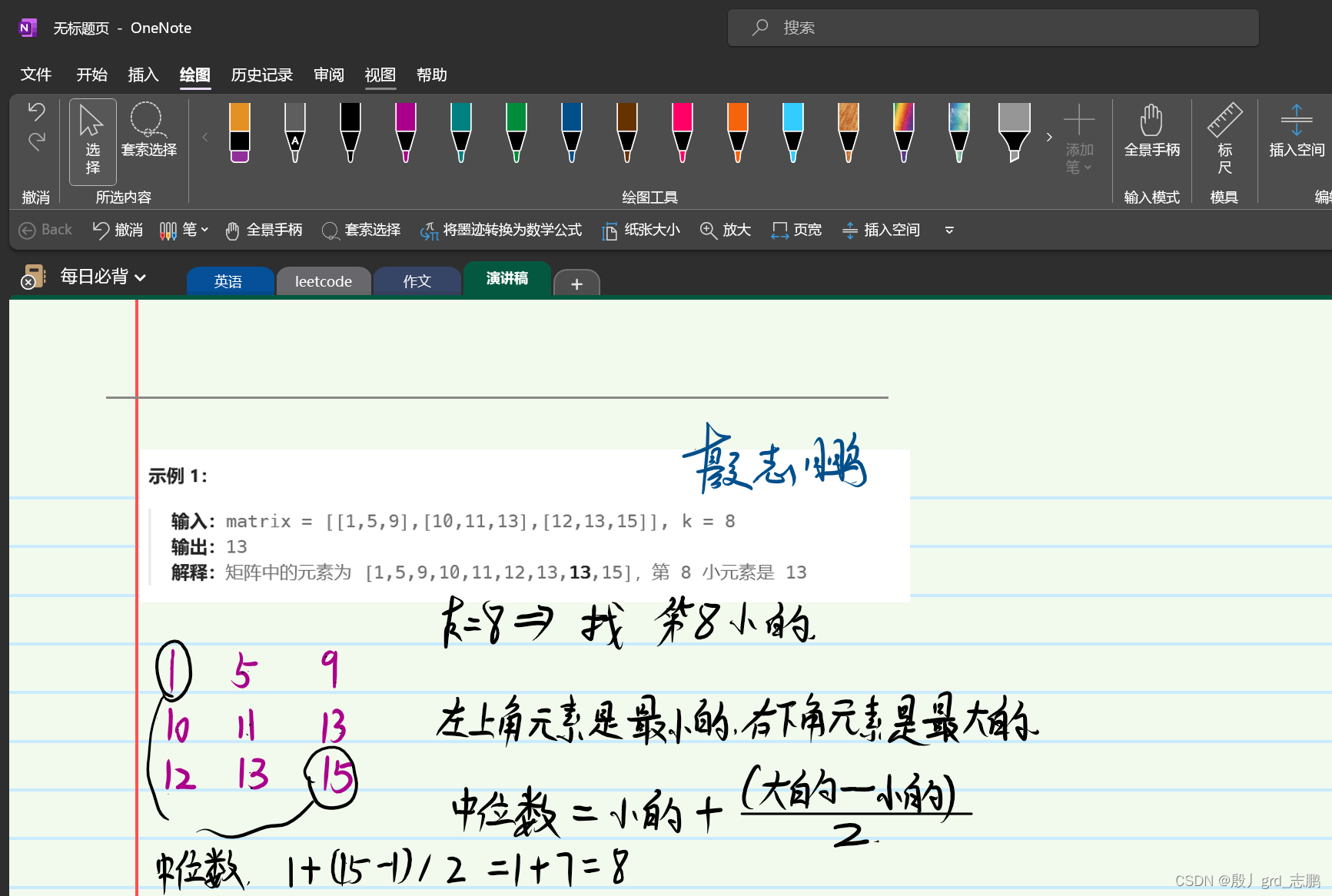
- 所以,随便划分一个矩形区域,左上角都是最小的元素,右下角都是最大的元素。
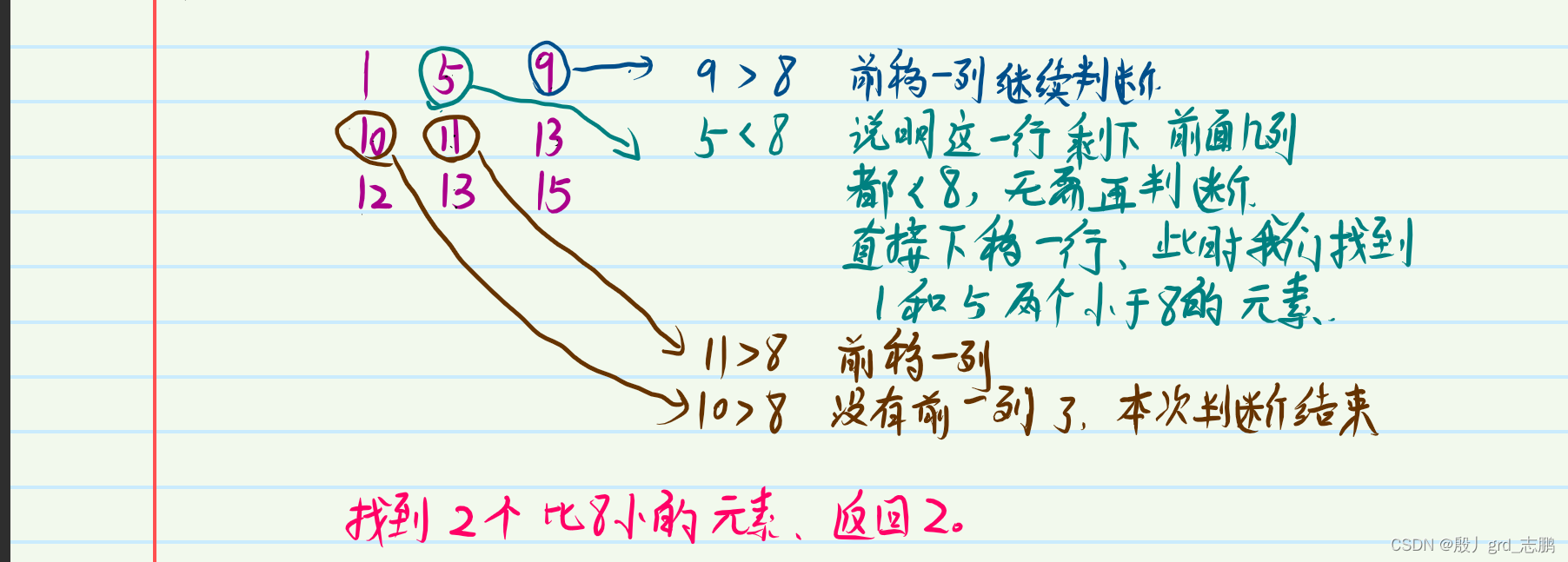
- 此时就有了两个边界,让我们来找到这个区域的最大值和最小值的中间值(不一定是矩阵中的元素)。然后判断,矩阵中元素谁比这个中间值小。只需要判断每行的后面的元素即可,因为每行递增排序,最后面的一定是最大的,如果最后一个比mid中间值小,那么这一行都比它小,如果倒数第2个元素比mid小,那么这一行前面的元素,一直从前往后到倒数第二个都比mid小。
| 代码:时间复杂度O( n ∗ l o g 2 r − l n*log_2{r-l} n∗log2r−l),二分查找进行次数为 O( l o g 2 r − l log_2{r-l} log2r−l),每次操作时间复杂度为 O(n). 空间复杂度O(1) |
|---|
class Solution {
public int kthSmallest(int[][] matrix, int k) {
int rows = matrix.length;//行数
int cols = matrix[0].length;//列数
int l = matrix[0][0];//左上角元素
int r = matrix[rows-1][cols-1];//右下角元素
while(l < r){//如果满足"小的" 不大于 "大的",就可以继续循环
int mid = l + (r-l)/2;//找到他俩的中位数
int count = checkValue(matrix, mid);//获取这个数在数组所有元素排好序后,它的相对位置
if(count < k){//如果这个数比目标值k小,说明我们应该在mid元素的右下区域找
l = mid+1;
} else {//否则在mid元素的左上区域找
r = mid;
}
}
return l;//最终,二分区域只剩一个元素或没有元素
}
public int checkValue(int[][] matrix, int mid){
int r = 0;//行下标
int c = matrix[0].length-1;//列下标
int count = 0;//计数
while(r< matrix.length && c >= 0){//如果行下标和列下标不越界就继续
if(matrix[r][c] <= mid){//如果当前元素比mid小
r++;//行需要进行下移,继续判断
count += (c+1);//既然下移了一行,那么就统计一行的元素,一行有c+1列,就有c+1个元素需要统计
//因为数组下标从0开始,c是当前二分区域的最后一列的下标,所以有c+1列
} else {//如果当前元素比mid还大,就说明没有我们要找的元素,让列前移一列
c--;
}
}
return count;//最终返回有几个元素比mid小。
}
}



![[足式机器人]Part2 Dr. CAN学习笔记- 最优控制Optimal Control Ch07-3 线性二次型调节器(LQR)](https://img-blog.csdnimg.cn/direct/752e69a984fb4469bc62cf813284fff9.png#pic_center)