技巧

1.判断得数为整数还是小数，可以%1，得数为0是整数  或者用instanceof

Integer number = 9; // 自动装箱
System.out.println(number instanceof Integer); // 输出：true

2.a * b = 最大公约数 * 最小公倍数

LCM 最小公倍数   GCD 最大公约数

A先/GCD是因为怕A*B的结果太大，因为GCD是最大公约数，所以能整除，不用怕有影响。 

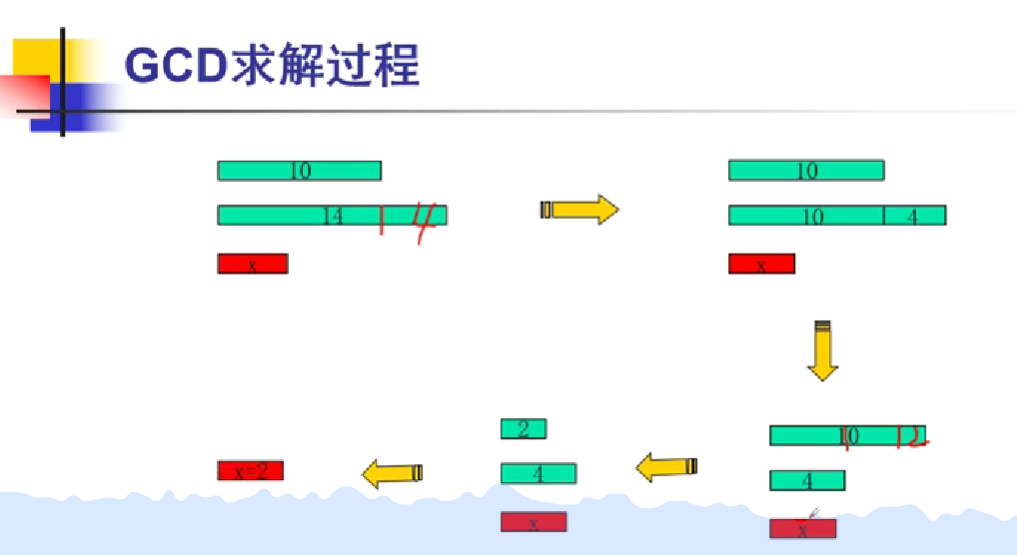
辗转相除法，也称为欧几里得算法（Euclidean Algorithm），是一种用于计算两个非负整数a和b的最大公约数的方法。该算法基于以下原理：两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数。辗转相除法通过重复应用相同的操作来实现这一目标：先用较大的数除以较小的数得到余数，然后将得到的余数作为新的除数再次进行除法运算，直到余数为零。此时，剩余的未变动的数即为两个数的最大公约数。

辗转相除法的计算过程可以通过以下步骤概括：

1. 初始条件：假设a和b都大于1且a>b。
2. 计算余数：将b除以a得到余数r1。
3. 更新余数：将余数r1除以a得到新的余数r2。
4. 继续迭代：重复步骤2和3，直到余数为零。