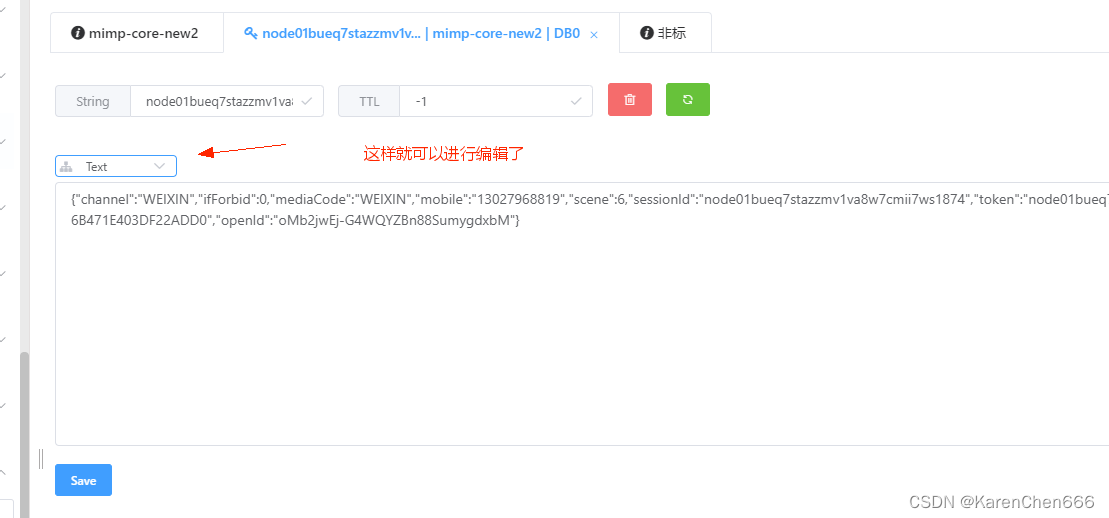
题目描述
游戏盘面是一个m行n列的方格矩阵,将每个方格用坐标表示,行坐标从下到上依次递增,列坐标从左至右依次递增,左下角方格的坐标为(1,1),则右上角方格的坐标为(m,n)。
游戏结束盘上只剩下一枚炮兵没有回到城池中,而兵棋恰好在盘面的左下角,它需要移动到右上角的城池中,游戏规定只能向上或向右移动,炮兵从左下角的方格中移动到右上角的方格中,每步移动一个方格。始终在方格矩阵内移动,请你计算出不同的移动路线的数目。
对于1行1列的方格矩阵,炮兵原地移动,移动路线数为1;对于1行2列(或2行1列)的方格矩阵,炮兵只需一次向右(或向上)移动,移动路线数也为1……对于一个2行3列的方格矩阵,如下所示:
(2,1) (2,2) (2,3)
(1,1) (1,2) (1,3)
炮兵共有3种移动路线:
路线1:(1,1) → (1,2) → (1,3) → (2,3)
路线2:(1,1) → (1,2) → (2,2) → (2,3)
路线3:(1,1) → (2,1) → (2,2) → (2,3)
输入
输入只有一行,包括两个整数m和n(0 < m+n ≤ 20),代表方格矩阵的行数和列数,m、n之间用空格隔开。
输出
输出只有一行,为不同的移动路线的数目。
样例输入1
2 3
样例输出1
3
提示/说明
标签
普及 其他 动态规划基础
动规的普通方法不是最优的
标数法是最优的

#include<iostream>
using namespace std;;
int main()
{
int m,n;
int a[20][20];
cin>>m>>n;
a[0][0]=0;
for(int i=1; i<=m; i++)
{
for(int j=1; j<=n; j++)
{
if(i==1||j==1)
{
a[i][j]=1;
continue;
}
a[i][j]=a[i-1][j]+a[i][j-1];
}
}
cout<<a[m][n];
return 0;
}