文章目录
- 📚介绍可视化
- 🐇什么是可视化
- 🐇科学可视化,信息可视化,可视分析系统三者之间有什么区别🔥
- 🐇可视化的基本流程
- 🐇可视化的两个基本设计原则
- 🐇数据属性
- 🐇可视化的基本图表🔥
- 📚可视化编码
- 🐇视觉编码
- 🐇基本图表🔥
- 📚图形感知
- 🐇前注意力机制
- 🐇格式塔学说
- 🐇变化盲视
- 🐇颜色感知
- 🐇颜色生成和颜色优化
- 📚可视化评估
- 🐇Edward Tufte设计准则🔥
- 🐇饼图、彩虹颜色表、3D图表的评价
- 📚高维数据可视化🔥
- 🐇为什么要降维
- 🐇多维尺度分析(Multidimensional Scaling/MDS)
- 🐇主成分分析(Principal Component Analysis/PCA)
- 🐇SNE
- 🐇T-SNE
- 📚层次可视化
- 🐇树可视化
- ⭐️节点链接式
- ⭐️空间填充式
- 🐇图可视化
- ⭐️force-directed算法🔥
- ⭐️node-link diagram
- ⭐️adjacency matrix
- 📚文本数据可视化
- 🐇动态文本
- 🐇文本可视化的流程
- 🐇文本可视化的方式
- ⭐️词云
- ⭐️树图
- ⭐️流图
- 📚标量场数据可视化
- 🐇间接体绘制
- 🐇直接体绘制
- 📚 交互
- 🐇交互的意义
- 🐇动态查询
- 🐇Brushing和linking
- 🐇overview + detail 和 focus +context 两种交互方式
📚介绍可视化
🐇什么是可视化
将非视觉的数据通过某种映射的方式(生成图像)串联视觉表达,生成可读可识别的结果,帮助用户高效地完成一些目标。
🐇科学可视化,信息可视化,可视分析系统三者之间有什么区别🔥
- 科学可视化侧重于使用计算机图形学来创建视觉图像,主要关注三维现象(具有天然几何结构的数据)的可视化,如建筑学、气象学、医学或生物学方面的各种系统,重点在于对体、面以及光源等等的逼真渲染,目的是以图形方式说明科学数据,这有助于理解科学概念或结果的复杂、通常是大规模的数字表示。
- 信息可视化是通过使用交互式可视化界面来传达抽象数据。抽象数据包括数字和非数字数据(抽象数据结构,如树状结构或者图形),如地理信息与文本,柱状图、趋势图、流程图、树状图等,这些图形的设计都将抽象的概念转化成为可视化信息。
- 可视分析是通过可视化交互界面促进的分析推理科学,主要挖掘数据背景的问题与原因,尤其关注推理和分析。
- 信息可视化与科学可视化的主要区别首先是:
- 科学可视化通常是观察基于物理的、有几何属性的数据,而信息可视化则用来显示各式各样的抽象数据;
- 其次,科学可视化的用户多是高层次的专业工作者,而信息可视化的用户则主要是非技术人员。要为难以形象表达的抽象数据设计更加容易理解的表现形式,使信息可视化面临更大的挑战。
- 信息可视化的可视化目的和科学可视化不同。
- 科学可视化的目的要求是真实地反映,要求忠实地“直译”。
- 而信息可视化的可视化目的则是要从大量抽象数据中发现一些新的信息,它不仅仅使简单的反映,而且要求能够创造性地反映,能够把隐藏在可视化对象深处或可视化对象之间的信息挖掘出来,它是一种知识和价值创造的过程,且信息可视化主要是通过使用交互式可视化界面来进行抽象数据的交流。
🐇可视化的基本流程
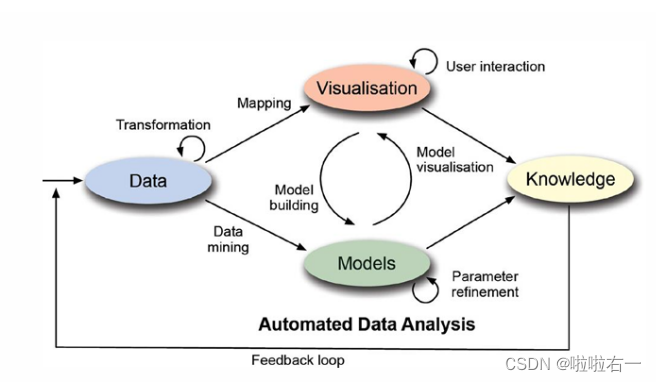
(说不清楚,直接画图)
🐇可视化的两个基本设计原则
- 简单性 (Simplicity):简单性是可视化设计的核心原则。它要求保持信息的简洁性和清晰性,以避免混淆和信息过载。
- 一致性 (Consistency): 一致性要求在可视化中使用一致的设计元素和规则,以创建统一的用户体验。
🐇数据属性

Nominal:标签类数据,比如男女,苹果、香蕉这些。Ordered:等级、排序。Interval:日期、坐标这种,没有0临界。Ratio:计数,有0临界,比如没有-4个人,–100岁。
🐇可视化的基本图表🔥
-
定性数据绘制
- 条形图(Bar Chart):显示每个类别的计数或相对频率。
- 饼图(Pie Chart):显示每个类别中整体的比例。
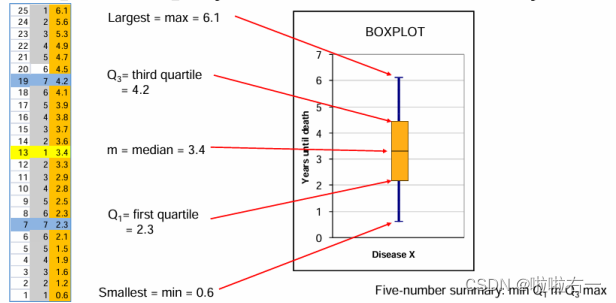
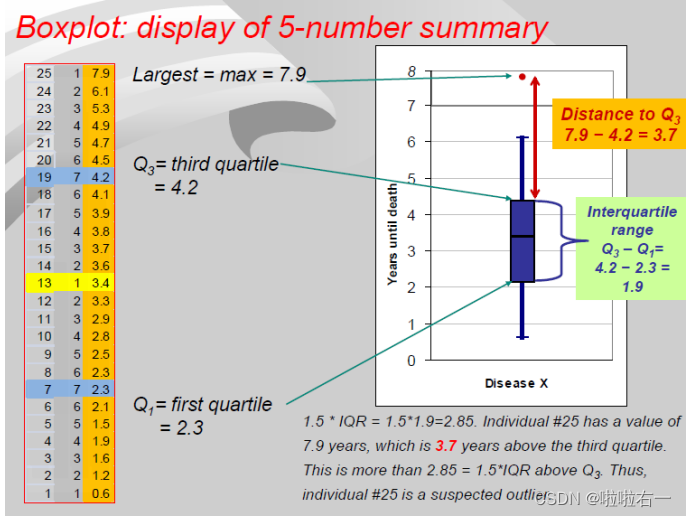
- 盒须图(Boxplot):箱线图是5-number summary(Minimum、Q1、median、Q3、maximum)的图形显示。
-
特点:可以反应原始数据 分布的特征,即可以从图中看出上边缘、下边缘、中位数、两个四分位数以及离群点,能提供有关数据位置和分散情况的关键信息。

-
构造步骤
- 构建一个以Q1和Q3作为头和尾的箱子,在箱子内部用横线标上中位数。(Q1和Q3的计算方法:数据分成一半后,两部分再分别求中位数就是Q1和Q3。如1、2、3、4、5、6:Q1就是2,Q3就是5。如22 25 34 35 41 41 46 46 46 47 49 54 54 59 60:Q1就是(35+41)/2=38,Q3就是(49+54)/2=51.5,注意这里算数据分成一半后的中位数是要把整体数据的中位数也算进去)
- 找出fences(fences),fence由1.5*IQR(
interquartile range (IQR) = Q3 –Q1)来决定,upper fences是在高于上四分位点1.5IQR的位置,lower fence是在低于下四分位点1.5IQR的位置。注意,fence只用于辅助构建箱型图,并不实际出现在箱型图中(upper fence和lower fence会出现)。 - 确定极大值极小值,从第一步构建的箱子的两端画线到极值。
- 用特殊符号表示超出上下限的数据离群值,且有时使用不同的符号表示距离四分位数超过 3 个 IQR 的“远异常值”
-
-
定量数据绘制
- 直方图(Histogram):频率分布直方图。
- 茎叶图(stem and leaf display)

📚可视化编码
🐇视觉编码
- 视觉编码是将数据映射到视觉变量的过程,不同的数据类型需要采用不同的编码方式来有效地传达信息。
- 视觉图元/标记(mark):点、线、面。
- 视觉通道(channel):位置、大小、形状、颜色、方向、纹理。

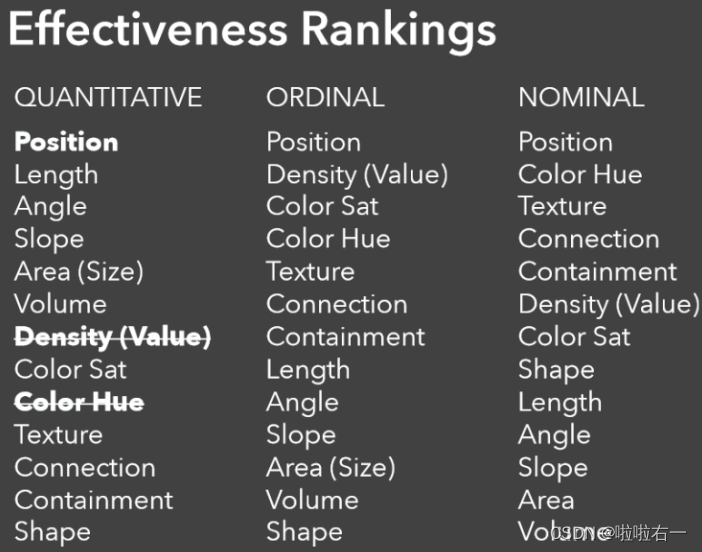
- Position、 Length、 Color Hue、 Shape 对于quantitative、nominal、ordinal三种数据的可视编码有效性排序🔥:
Quantitative: Position Length Color Hue shapeNominal: Position Color Hue Length shapeOrdinal: Position Color Hue Shape Length
多维数据

🐇基本图表🔥
- 雷达图/星图(Radar Plot / Star Graph):显示多个定量变量的图表。
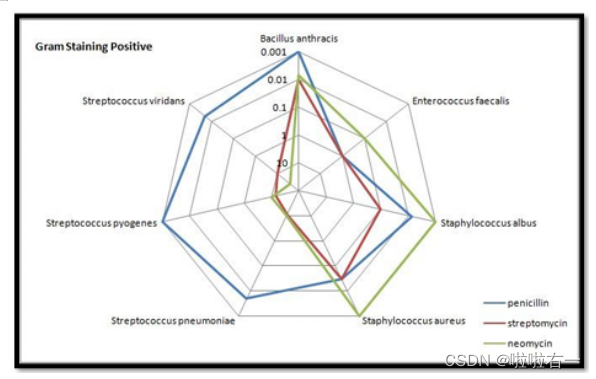
- 优点:
- 可以同时展示多个变量,方便比较不同类别或对象在这些变量上的性能;
- 可以用来评估一个实体在多个维度上的平衡性或一致性;
- 易于通过叠加多个雷达图来比较不同实体或组之间的差异。
- 缺点:
- 当变量数量过多时,雷达图会变得杂乱且难以阅读;
- 对于相隔较远的轴,比较就变得比较困难;
- 变量的值需要经过适当的归一化或标准化处理,否则直接比较可能没有意义。
- 优点:
- 平行坐标系(Parallel Coordinates):由一组平行的轴构成,每个轴代表数据集中的一个维度,并且所有轴之间等距排列。数据点在平行坐标系中通过一系列连线表示,每根连线表示数据集中的一个记录,而连线在每个轴上的位置则对应那条记录在该维度上的值。
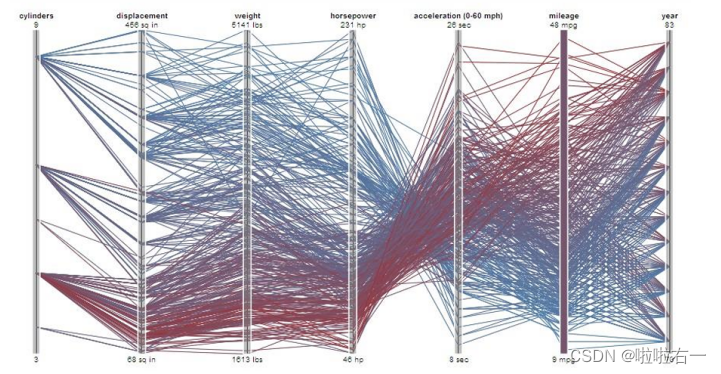
- 优点:
- 可以揭示不同维度之间的关系,适用于高维数据集;
- 通过观察数据点的趋势线,可以识别变量之间的关系和潜在的数据模式。
- 缺点:
- 过于密集的线条可能会造成视觉上的混乱;
- 轴线的排序会影响可视化的可读性和解释性。
- 优点:
- 散点图(Scatterplot Matrix(SPLOM)):显示多维数据集中各维度之间的变量两两关系的图形表示方法。在一个矩形的网格中排列散点图,网格的行数和列数等于选定变量的数量。网格的每一行和每一列对应数据集的一个特定变量。对于网格中的每个单元格来说,横轴是该单元格所在列对应的变量,纵轴是该单元格所在行对应的变量。在对角线位置(横纵轴变量相同的位置),通常显示轴变量的单变量分布。
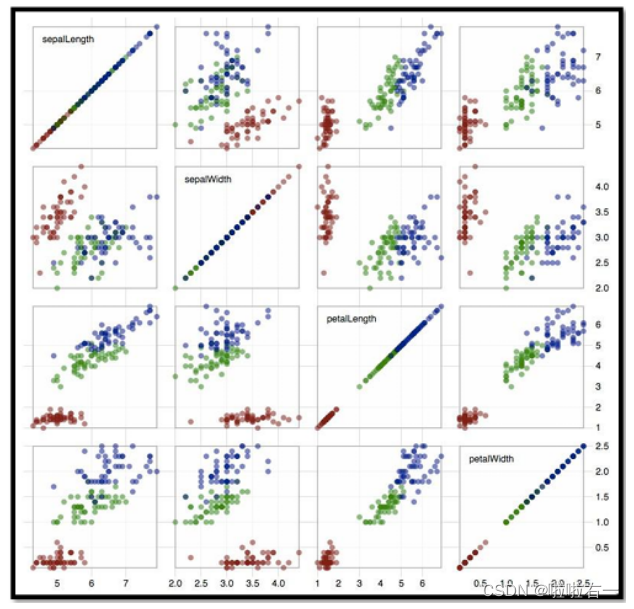
- 优点:
- 可以揭示出多个维度的变量两两之间的相关性和模式;
- 可以帮助识别数据中的异常值或异常点;
- 对角线可用于显示各个变量自身的分布。
- 缺点:
- 当变量的数量非常多时,散点图矩阵也可能变得非常复杂并难以解读;
- 绘制散点图矩阵可能需要大量计算资源;
- 只能显示两个变量之间的关系,不能直接表示多个变量之间的交互作用。
- 优点:
📚图形感知
- 图形感知是可视化设计中非常重要的一个方面,它指的是人们对于不同图形属性的感知能力。在可视化设计中,利用图形感知的原理可以帮助我们更好地传达信息,提高用户对数据的理解和分析能力。
🐇前注意力机制
- 前注意力机制指的是人们在观察图像或图形时的注意力集中。在可视化设计中,我们可以通过设计突出性的元素或使用色彩对比等方式来引起用户的前注意力。这有助于用户更快地获取信息并准确理解数据。

🐇格式塔学说
-
接近性:相互靠近的元素被认为是一个群组,与其他元素区分开。例如,在一个散点图中,如果在相同的区域内有多个点,我们会将它们视为一组并与其他点分开。
-
相似性:具有相似特征的元素往往被认为是一组。例如,在一个柱状图中,具有相同颜色或形状的柱子被视为一组并传达同样的信息。
-
连通性:连通性超过了接近度、大小、颜色形状。
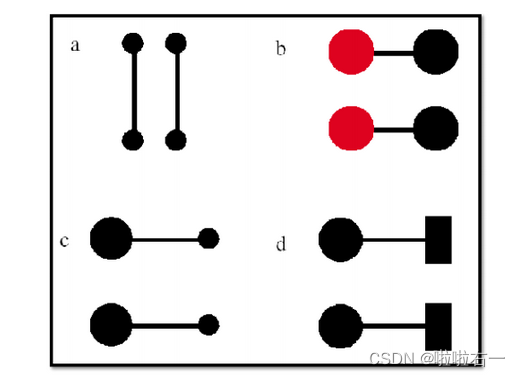
-
连续性:在视觉上连续的元素往往被认为是一组。例如,一条连续的曲线通常表示一条数据趋势,而离散的点通常表示单独的数据点。
-
封闭性:具有边缘或形状的闭合元素往往被认为是一个整体。例如,一个有边界的面积图形表示一个特定的数据集,而没有边界的散点图表示一系列独立的数据点。
-
对称性
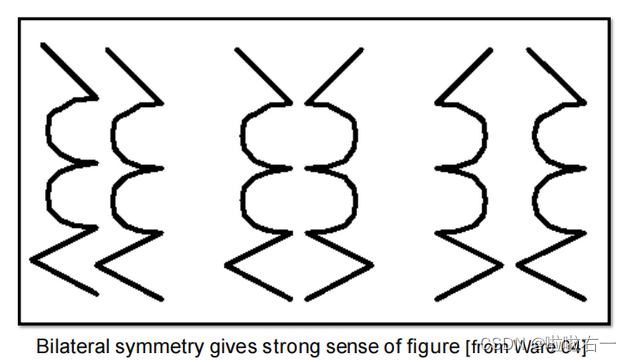
-
简单性:人们更容易理解简单、直观的形状和图形。例如,在可视化设计中,简单的线条、图标和图形通常比复杂的图形更易于理解和解释。
🐇变化盲视
- 变化盲视是指人们在观察连续变化的图形时,可能会忽视其中的细微变化。在可视化设计中,我们需要注意这一现象,避免在数据变化时导致用户错失重要信息。设计中可以使用动画或其他方式来突出变化,帮助用户更好地感知和理解数据。

🐇颜色感知
- 颜色感知的基本流程
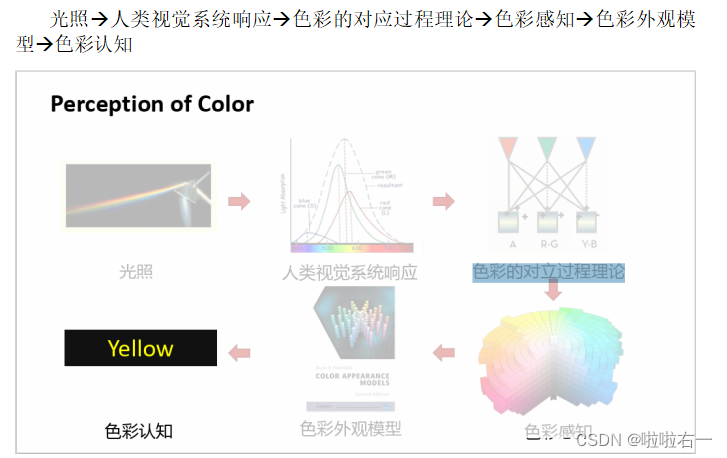
🐇颜色生成和颜色优化
- 颜色生成(Color Generation)
- Palettailor:分类数据的可区分着色。
- 多类散点图的交互式上下文保留颜色高亮显示。
- 颜色优化(Color Optimization)
- 优化颜色分配,以感知多类散点图中的类可分离性。
- 数据驱动的颜色图调整,用于探索标量场的空间变化。
- 区别:前者关注的是根据数据和可视化的需求来创建和分配新的色彩方案,后者关注的是改进和调节现有色彩的使用;
📚可视化评估
🐇Edward Tufte设计准则🔥
-
图形完整性(Graphical Integrity):确保图表能够准确地传达数据的信息,不夸大或歪曲数据。
- 图形应当包含所有必要的标签和轴来消除图形失真和歧义;
- 图形应当使用一致的比例;
- 图形中的样本大小应当对结果具有代表性或权重;
- 数字的表示应与测量的数值成正比。
-
谎言因子(The lie factor):避免使用图表中的元素尺寸或位置比例不准确地传达数据。
- 用来衡量图形中存在的数值误导或误导程度的指标,通过比较图形中视觉元素(如长度、面积等)的变化与对应数据的实际变化之间的比例来计算的。
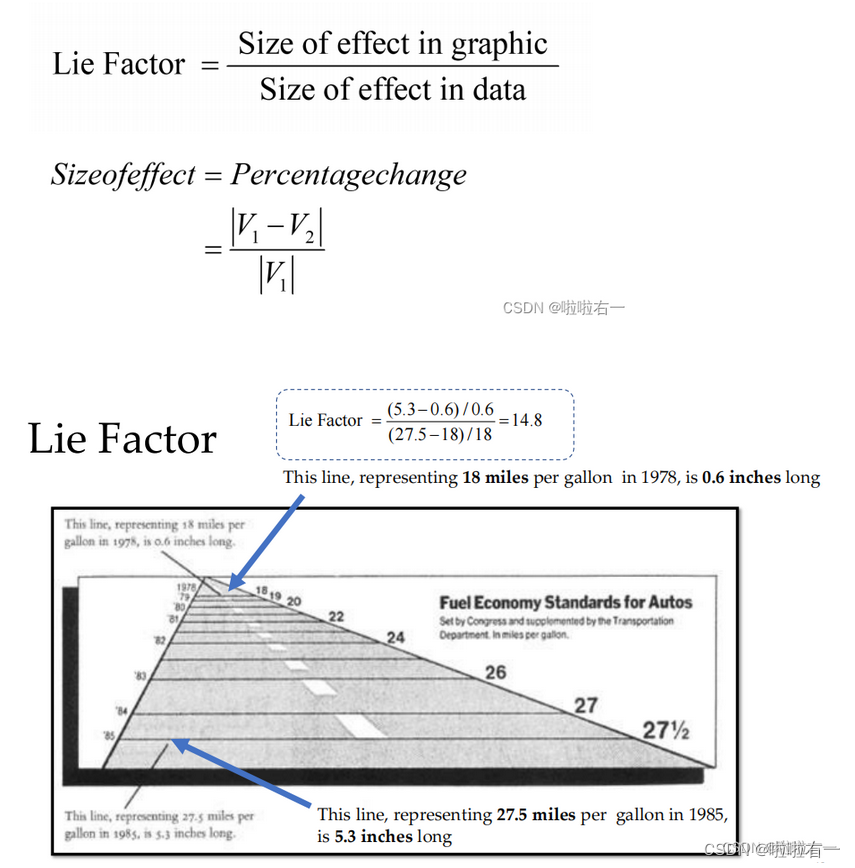
- 用来衡量图形中存在的数值误导或误导程度的指标,通过比较图形中视觉元素(如长度、面积等)的变化与对应数据的实际变化之间的比例来计算的。
-
数据墨水笔(data-ink):最大化数据墨水的使用,即减少非必要的图形元素,使得数据更突出。
- 删除或最小化不必要的装饰性元素,如背景图案、阴影、边框等,使图形更加简洁、精确地传达数据信息。
- 两个擦除原则:在合理范围内擦除非数据墨迹;擦除冗余数据墨迹。
- 五大原则:
- 最重要的是显示数据;
- 最大限度地提高数据墨水比;
- 擦除非数据墨迹;
- 擦除冗余数据墨迹;
- 修改和编辑。
-
图表杂乱(Chart Junk):避免在图表中添加无意义的装饰元素,保持简洁性和清晰性。
- 指的是图表中那些多余、无意义或过度装饰的元素,比如网格、阴影、3D效果、过多的装饰线条、繁琐的图例等。
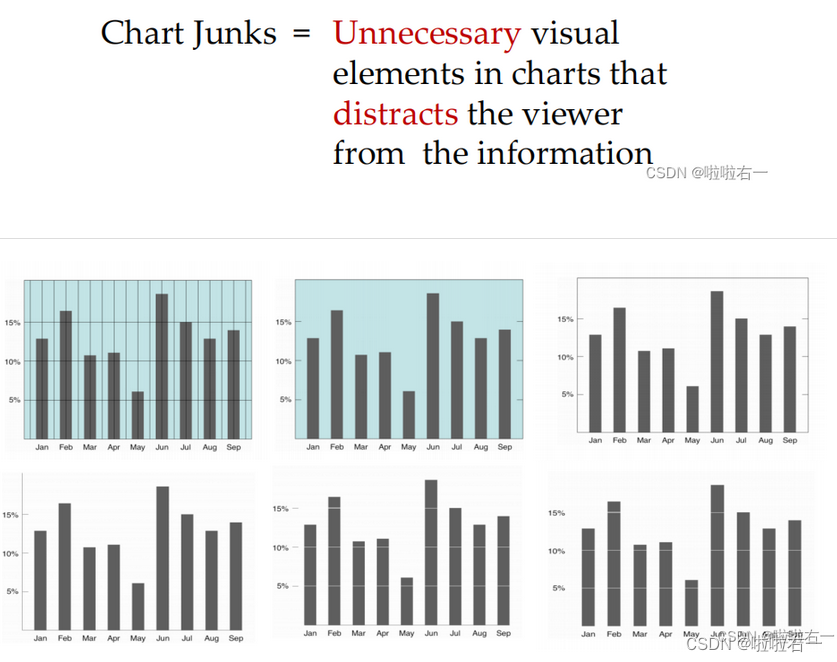
- 指的是图表中那些多余、无意义或过度装饰的元素,比如网格、阴影、3D效果、过多的装饰线条、繁琐的图例等。
- 使用bar chart需要数据有零值线。
- 使用line chart主要比较的是数据的趋势或是线条与水平线的角度。
🐇饼图、彩虹颜色表、3D图表的评价
- 饼图
- 适用场景:适用于显示数据类别较少的数据部分和整体的关系。
- 优点:
- 直观地以图形方式表现出每个部分与总体的大小关系;
- 构造简单,节省空间;
- 利用不同的颜色来区分数据的不同类别,增强视觉效果。
- 缺点:
- 当数据点过多或者数据差异不明显时,表现力很差;
- 在比较各个部分之间的细微差别时效果不佳;
- 无法用来展现数据的时间变化或趋势;
- 对于同一个数据集,通过调整数据的顺序或方式,可能会导致误导。
- 彩虹颜色表:将数据映射到一系列连续色彩变化的颜色表。
- 适用场景:适用于显示分类数据,有序类别或数值数据以及具有中点意义的数值数据。
- 优点:
- 提供明亮多彩的视觉效果,可以吸引注意力;
- 可以区分数据的不同范围,尤其是在色带变化明显的地方;
- 能够利用颜色的多样性表现广泛的数据范围。
- 缺点:
- 色调变化在感知上并不均匀,某些颜色(如黄色或青色)在视觉上跳跃比其它颜色(如蓝色或红色)更显著,可能误导数据的解读;
- 由于色带变化不一致,低对比度的区域可能会隐藏数据中的重要特征。
- 人们对用颜色表示的极端数据缺乏感知
- 低亮度颜色(蓝色)可能会隐藏高频值
- 3D图表
- 适用场景:适用于展示物理空间、体积或者三维关系的数据(如建筑设计图、分子结构模型等)。
- 优点:对于某些数据集(例如体积、地形或其他空间关系的数据),有助于直观理解其结构。
- 缺点:视觉失真可能导致误读数据,精确值难以读取。
📚高维数据可视化🔥
🐇为什么要降维
- 高维数据难以可视化;
- 排除不重要的特征,从而提高模型的效率和准确性;
- 降维,可以降低计算复杂度;
- 降维可以选择最具代表性的特征来减少相关性或冗余性。
🐇多维尺度分析(Multidimensional Scaling/MDS)
-
主要思想:
- 通过计算数据点之间的距离矩阵,并尝试在低维空间中重新构建数据点之间的距离矩阵。
- 具体来说,MDS算法首先计算原始数据点之间的距离,然后通过优化算法在低维空间中找到合适的投影,使得在低维空间中的距离与原始距离最接近。
- 即以距离为标准,将高维坐标中的点投影到低维空间中,保持点彼此之间的相似性尽可能不变。

优点 缺点 不需要先验知识,计算简单; 如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果。 保留了数据在原始空间的相对关系,可视化效果比较好。 各个维度的地位相同,无法区分不同维度的重要性。
🐇主成分分析(Principal Component Analysis/PCA)
-
主要思想:
- 使用特征值分解来寻找数据中具有最大方差的主成分。PCA将高维数据通过线性变换映射到低维空间,并保留了最重要的特征。
- 即:找到能让数据降维后数据间的方差最大的轴,将数据线性的投影到该轴上,投影后的特征称为主成分。
-
流程:PCA算法首先创建一个数据矩阵,然后通过减去均值来将数据中心化。接下来,它计算数据的协方差矩阵,并找到该矩阵的特征向量和特征值。最后,PCA算法根据特征向量将数据映射到新的低维空间。
优点 缺点 使得数据集更易使用; 如果用户对观测对象有一定的先验知识,掌握了数据的一些特征,却无法通过参数化等方法对处理过程进行干预,可能会得不到预期的效果,效率也不高; 正交算法,降低算法的计算开销,速度快; 降维后数据的邻域点与原来空间中的邻域点可能不同; 去除噪声; 特征值分解有一些局限性,比如变换的矩阵必须是方阵; 使得结果容易理解;完全无参数限制。 在非高斯分布情况下,PCA方法得出的主元可能并不是最优的。
🐇SNE
-
基本思想:SNE算法的基本思想是通过最小化KL散度来在低维空间中表示高维数据的相似性,通过仿射变换将数据点映射到概率分布上。
-
主要步骤:SNE构建一个高维对象之间的概率分布,使得相似的对象有更高的概率被选择,而不相似的对象有较低的概率被选择;SNE在低维空间里在构建这些点的概率分布,使得这两个概率分布之间尽可能的相似。
优点 缺点 能较好地保持高维数据的局部结构; 计算开销大; 适合于揭示高维空间中紧密聚集数据的聚类结构。 对算法超参数敏感; 改变了MDS中基于距离不变的思想,将高维映射到低维的同时,尽量保证相互之间的分布概率不变。 可能受到拥挤问题影响,导致不同的数据点在低维空间堆叠。 -
拥挤问题:由于没有考虑不同类间的间隔,因此会导致结果比较拥挤。各个簇聚集在一起,无法区分。 拥挤问题就是说降维后各个簇聚集在一起,无法区分。比如有一种情况,高维度数据可以分开,降维到低维就分不开了,MDS和SNE都存在。
- PCA是线性降维,MDS是非线性的,PCA和MDS都是global,TSNE是非线性且local的方法。
- MDS和SNE都有拥堵问题,降维中怎么解决拥堵问题——T-SNE通过将SNE中低维空间的高斯分布转换为t分布来解决。
🐇T-SNE
-
基本思想:将数据点之间的相似度转化为条件概率,原始空间中数据点的相似度由高斯联合分布表示,嵌入空间中数据点的相似度由t分布表示。将高维空间中的数据映射到低维空间中,并保留数据集的局部特性。
-
相比SNE主要改动:使用对称版的SNE,简化梯度公式; 低维空间下,使用
t分布替代高斯分布表达两点之间的相似度。
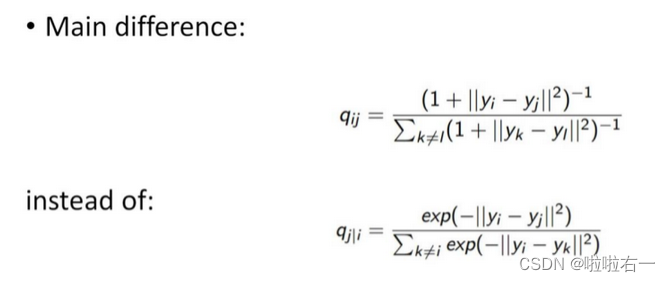

优点 缺点 能在不同规模数据集下展现高维数据点的聚类; 速度慢,占用内存; 可以减轻拥挤问题。 没有唯一最优解,且没有预估部分。

t-SNEVSPCA- 目标函数:t-SNE 的目标是保留数据点之间的相似关系,强调保持局部结构,而不强调保持全局结构。PCA 的目标是通过线性变换找到投影方向,使得数据在各个主成分上的方差最大化。
- 非线性映射:t-SNE 使用非线性映射,可以更好地处理非线性关系,能够将高维空间的复杂结构映射到低维空间。PCA 使用线性映射,只能捕捉到数据中的线性相关性。
- 数据量:t-SNE 在处理大规模数据集时比较耗时,计算复杂度较高。PCA具有快速计算线性变换的优势,在处理大规模数据时更高效。
- 数据显示:t-SNE 在降维后往往保留了数据中的局部结构,更适合展示数据的类别聚类等局部特征。PCA 则更适合于捕捉整体的线性相关性。
- 总结来说,t-SNE 算法通过非线性映射将高维数据映射到低维空间,并保留数据之间的相似性关系,强调保持局部结构。与之相比,PCA 算法使用线性映射来找到投影方向,最大化数据在主成分上的方差,并更适合于捕捉整体的线性相关性。
📚层次可视化
🐇树可视化
⭐️节点链接式
- 节点分布在空间中,通过直线或曲线连接,用二维空间分解广度和深度,空间用来表达等级取向。容易造成深度或宽度上的指数增长。
- 适用场景:适用于分支结构比各个节点具体值更重要以及层次结构和分支关系较为明确的树。
- 优点:直观地呈现树的父子关系、层次结构和分支关系。
- 缺点:
- 树的规模较大时,容易产生混乱的交叉连接线,导致可视化效果不佳;
- 难以编码多个变量的数据情况;
- 大量节点聚集在屏幕的局部范围,屏幕空间的利用率底下。
- Tidy layout:让兄弟节点之间保持等距,父节点位于其子节点的中轴线上。
- 文件目录树
- 优点:使用缩进来表现文件的目录结构,用户使用折叠和展开操作,可以快速地对文件结构进行浏览并定位文件的位置。
- 缺点:
- 可扩展性不高:文件目录较多时,一次只能显示一部分,常常需要大量的滚动,给文件定位带来困难。
- 广度和深度争夺空间,且常常因过多文件名挤占空间无法显示。
- 应用: 常用场景是文件目录结构
⭐️空间填充式
- 适用场景:适用于需要紧凑地显示树形结构,并强调节点大小关系的场景。例如,展示各个类别销售额占比的树图。
- 优点:
- 能够更好地利用空间,降低视觉混乱的可能性;
- 擅长表示包含与从属的关系。
- 缺点:
- 不太直观地显示树的分支结构和层次关系;
- 不太适合展示大量详细信息,如节点的属性或标签。
- treemap🔥
- 是一种空间填充表示,每一项所占面积表示了节点大小,每个子树用一个矩形表示,该矩形被划分为与子树相对应的小矩形。对于每个孩子递归重复切片,将切片方向从垂直方向转换为水平方向或相反方向。使用区域编码数据项的其他变量。
- 基本步骤:
- 定义一个矩形区域作为根节点。
- 计算根节点内每个项目的面积。
- 根据项目的面积比例,在根节点内按比例划分新的矩形子区域,并将项目填充到相应的子区域中。
- 递归地对每个子区域重复步骤2和步骤3,直到所有项目都被安排在矩形区域内。
- 优点:
- 提供整个树的单一视图更容易发现大/小节点;
- 很好的表示节点链接之外的两个属性:color和area;
- 可以较好的表示树的大小属性和浅层次;
- 树状图更适用于组级比较;
- 易于实现和理解,可应用于大量项目。
- 缺点:
- 难以准确读取结构/深度;
- 信息密度问题:在生成大量项目的 Treemaps 时,小项目可能会因为太过密集而难以辨认和阅读。
- 项目重叠问题:由于矩形区域的限制,可能导致项目之间存在重叠,降低了可视化效果。
- 不擅长表现结构,对于大的树的可视化会占用大量面积;
- 难以找到好的纵横比;
- 不好显示除父子关系之外的链接
- 仅支持单个项目的可视化搜索;
- 人们对treemap所使用的面积形式通常难以比较大小。
- 难以准确读取结构/深度;
- 应用:可以用在文件目录结构、软件图表、大小查询的地方。
对比treemap和普通的树形文件系统,分别能执行什么任务不能执行什么任务?
- Treemap(矩形树图):Treemap通过在一个矩形区域内以矩形的大小和颜色来表示文件和文件夹的层次结构。这种可视化方式使得用户可以更直观地理解文件和文件夹的相对大小和分布情况。
- 任务:Treemap适用于快速了解和分析大量文件和文件夹的层次结构。它可以帮助用户识别特定文件或文件夹在整个层次结构中的位置和重要性,以及了解各个层级之间的关系。
- 不能执行的任务:Treemap的主要局限在于不适合处理深层次且包含大量节点的树状结构。当树的层级很深,并且节点数量庞大时,矩形树图可能变得非常复杂和拥挤,并且难以准确表示所有节点。
- 普通的树形文件系统:普通的树形文件系统以层级关系展示文件和文件夹。每个文件夹可以包含其他文件夹和文件,用户可以通过展开和收起文件夹来查看和访问特定的文件。
- 任务:普通的树形文件系统适用于组织和浏览文件和文件夹,以及进行文件和文件夹的操作和管理。它可以帮助用户快速定位和访问特定的文件或文件夹,以及在层级结构中移动和操作它们。
- 不能执行的任务:普通的树形文件系统相对于Treemap而言,在可视化方面较为简单,无法提供更复杂的数据分析和比较功能。它也不适合在大规模文件和文件夹集合中查找和识别特定的文件。
🐇图可视化
⭐️force-directed算法🔥
-
主要算法:一开始对节点的位置进行随机初始化,定义所有节点之间存在斥力,相邻节点之间存在引力,然后开始按照节点之间两种力相互作用的结果重新确定节点之间的位置,每变换一次位置就要对力进行重新计算,一直迭代计算直到节点之间的位置不再改变或是改变幅度小于某个给定的值才结束。

- 随机分布初始节点位置;
- 计算每次迭代局部区域内两两节点间的斥力所产生的单位位移(一般为正值);
- 计算每次迭代每条边的引力对两端节点所产生的单位位移(一般为负值);
- 步骤 2、3 中的斥力和引力系数直接影响到最终态的理想效果,它与节点间的距离、节点在系统所在区域的平均单位区域均有关,需要开发人员在实践中不断调整;
- 累加经过步骤 2、3 计算得到的所有节点的单位位移;
- 迭代 n 次,直至达到理想效果。
-
缺点:迭代的步长不易确定,步长太大会导致形成的合力太大,可能会造成系统的震荡,不易达到平衡稳定的体系;步长太小会导致迭代步需要合并;速度慢,时间复杂度过高,为 O ( n 3 ) O(n^3) O(n3),排斥力的时间复杂度为 O ( n 2 ) O(n^2) O(n2);如果图中的节点和连接边的数量过多会导致边的交叉问题。
-
改进:
使用距离的平方和进行比较、计算,避免开方计算;- 排斥力计算的时间复杂度过高(O(n^2)),使用
Barnes-Hut算法通过聚合粒子来估算粒子之间相互的斥力,具体使用四叉树实现,最后优化的算法复杂度为O(nlgn)(每一个非叶节点表示一组相近的物体。如果一个非叶子节点的质心离某个物体足够远,那么就将树中那个部分所包含的物体近似看成一个整体,其位置就是整组物体的质心,其质量就是整组物体的总质量。如果非叶子节点离某个物体并不足够远,那么就递归地遍历其所有子树。); GEM算法通过减少一个temperature参数来允许点在迭代早期移动大的距离后期移动小的距离来加速;- 在两个节点之间距离为0的时候随即产生一个小力将二者分开防止当二者有相同邻居时会一直贴合在一起;
- 可以将距离为n条边的节点之间建模为长度为nL的弹簧来消除斥力以减小计算时间。

⭐️node-link diagram
- 优点:容易看到两点之间的路径关系和是否连接。
- 缺点:线条之间容易交叉,会有阻挡、当连接的边和点变多时会混乱、在展示形式上有方向、度量、形状上的限制。
⭐️adjacency matrix
- 优点:容易看到两个点是否连接、不存在线条之间的交叉、能在矩阵条目中显示每个边相关的其他信息。
- 缺点:行和列的顺序极大影响了解释矩阵的难易程度、很难看到两个点之间的路径、所占用的空间很大(O(n^2)的矩阵)、受屏幕分辨率的限制。
- 可视化设计的常用方法
- 缩进——线性列表,缩进编码深度
node-link diagram——由直线/曲线连接的节点enclosure diagrams——用外壳表示层次结构layering——相对位置、大小和对齐来表示关系和大小
📚文本数据可视化
🐇动态文本
通过添加时间维度或交互能力来展示和探索文本数据。动态文本可视化侧重于呈现文本数据随时间或用户行为的变化,与静态文本可视化相比,它允许用户更深入地理解和分析数据。
🐇文本可视化的流程
文本数据获取、分词,文本数据特征提取,文本数据结果呈现。
🐇文本可视化的方式
⭐️词云
- 呈现文本数据的关键词。它通过使用不同字体大小来表示词语的重要性,以直观的方式展示关键词的频率分布。
- 优点:直观,可以通过大小比较词语出现频率和重要性。
- 缺点:信息不全面、缺乏量化分析、容易失真、受算法和数据处理影响。
- 适用场景:适用于展示关键词和揭示文本中的主题。
⭐️树图
- 将文本数据以树状结构展示的图表形式。
- 优点:层次结构清晰,可扩展性好。
- 缺点:对于非层次数据不太适用;数据集较为复杂时,图形展示不够清晰。
- 适用场景:树图适用于展示组织结构、文件目录、分类关系等层次结构的数据。
⭐️流图
- 通过标准化的符号和箭头来展示一个过程中的各个步骤及它们之间的关系。
- 优点:可以清晰地展示文本中信息的流动顺序或时间序列事件的变化过程;能够有效地表示文本中不同实体或概念之间的相互作用和转换。
- 缺点:展示文本时可能无法充分表示文本的深层意义或语境中的细微差别。
- 适用场景:用于体现信息在文档中如何流转。
📚标量场数据可视化
🐇间接体绘制
- “标量场”是指一个定义在空间中每一点上都有单个数值的函数。
- Marching squares算法:用于等值线提取。
- 将二维标量场划分为与像素网格对齐的正方形(或“单元格”);
- 计算每个单元格四个角点的标量值;
- 确定单元格角点值相对于所需提取的等值线值的位置(即角点值是在等值线值之上、之下还是正好就是等值线值);
- 使用查找表确定当前单元格内等值线的基本几何形状,查找表基于单元格四个角点的值;
- 连接相邻单元格中的等值线段,创建一个连续的线。

🐇直接体绘制
- “直接”体现在不需要提前提取表面(如等值面)或结构,而是直接在体积数据上进行渲染。
- Ray casting算法:
- 射线生成:从虚拟摄像机的视点发出射线,穿过屏幕平面上的每一个像素点,并进入体数据(voxel grid)。
- 采样:在每条射线上,沿着视线方向在固定间隔或自适应间隔采样标量场数据。这些采样点的值通常使用插值方法(例如最近邻、线性插值)从周围的体元(voxels)中得出。
- 传输函数映射:使用传输函数将每个采样点的标量值映射到颜色和不透明度(opacity)。传输函数是科学可视化中的核心概念,它定义了如何将数据值转换为可视化中的颜色和材料属性。
- 颜色合成:按照射线方向,将采样点的颜色和不透明度合成到最终像素颜色中。这通常通过“前向走样”(front-to-back compositing)或“后向走样”(back-to-front compositing)的方式完成。在这个过程中,根据合成模式(如alpha blending),通过叠加颜色和不透明度来构建最后的颜色值。
- 图像生成:将计算得到的像素颜色值显示到屏幕上,形成最终的可视化图像。
- 颜色表:通常是一种将标量值映射到颜色的查找表或函数,让不同的数据值显示为不同的颜色。
- 不透明度(或称之为可容差,compacity):是另一种函数或表,它定义了数据值到不透明度的映射,以确定渲染像素的不透明程度,进而影响最终图像的能见度。

📚 交互
🐇交互的意义
- 能够针对任何用户的操作提供快速、可逆、可持续的反馈;
- 允许用户首先提出一个概述,之后按需提供细节。
🐇动态查询
- 动态查询是对象和动作的视觉表示,是快速渐进和可逆的动作,能立即和连续的显示结果,并且是通过指向选择无需打字。
- 优点:快速、简便、可逆、可以消除杂乱、可以看到样例的出现和消失。
- 缺点:
- 无法进行布尔查询;
- 过滤器占用空间;
- 当数据集变大时查询变慢。
🐇Brushing和linking
- 都将指代同一数据的多个视图链接起来。
- 基本功能:
- 在某一个视图中选择突出显示的案例,在其他视图中也突出显示;
- 移动鼠标到案例上,可以显示同一个数据在多个视图之间的对应关系;
- 对一个视图中做到更改,在其他的视图中也会被修改。
- Linking:一个视图中选出一个数据,其他视图中的该部分也会被选中,起到连接不同视图的作用。
- Brushing:直接光柱数据的一个子集,起到选择的作用。
🐇overview + detail 和 focus +context 两种交互方式
- 焦点方式不同 ,交互方式不同,使用场景不同
- Overview + Detail 旨在通过提供全局概览和详细信息的同时,帮助用户更好地理解大规模的数据集。
- 多个视图展示,相同的数据,不同的分辨率,且视图之间空间分离。
- 能够快速导航到要找的地方,并且不会改变细节信息
- 细节改变会立即显示在概览中
- 为查看者提供更多信息以及有关数据用例的详细信息。可以获得更多关于具体事件的信息,但是可能造成从聚集视图到个人视图的改变,缩放可能不能呈现所有的信息,或者令数据变得抽象
- Focus + Context 通过提供关注区域的详细信息和整体背景信息(上下文)来帮助用户理解特定部分的数据。
- 同一个视图中同时包含焦点和焦点周围的环境
- 显示细节时保持用户方向
- 数据大时有问题
- 将选定的特定事件集合信息嵌入到整体当中,视图包含局部信息和整体信息。方法减少了过滤和聚合的数据量,但是需要为呈现具体事件的视图挪出空间,可能导致整体信息的变化,造成几何上的扭曲,比如相关数据的比例关系发生变化等。