适用平台：Matlab 2023版及以上

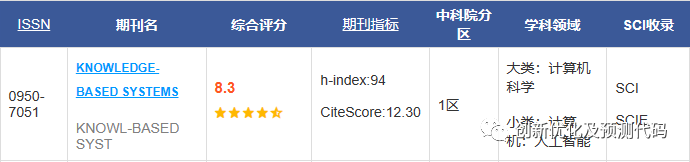
KOA开普勒优化算法，于2023年5月发表在SCI、中科院1区Top顶级期刊《Knowledge-Based Systems》上。

该算法提出时间很短，目前还没有套用这个算法的文献。

同样的，我们利用该新鲜出炉的算法对我们的CNN-BiLSTM-Attention时序和空间特征结合-融合注意力机制的回归预测程序代码中的超参数进行优化，构成KOA-CNN-BiLSTM-Attention多变量回归预测模型.

这篇论文介绍了一种名为开普勒优化算法（Kepler optimization algorithm，KOA）的新型元启发式算法，并对其进行了评估。KOA算法受开普勒行星运动定律的启发，旨在解决连续优化问题。在KOA中，每个行星及其位置代表一个候选解，通过根据迄今为止的最佳解（太阳）进行随机更新来实现优化过程，从而更有效地探索和利用搜索空间。通过使用各种基准问题对KOA算法的性能进行评估，并与其他随机优化算法进行比较。结果表明，KOA在收敛性和统计数据方面优于其他优化器。

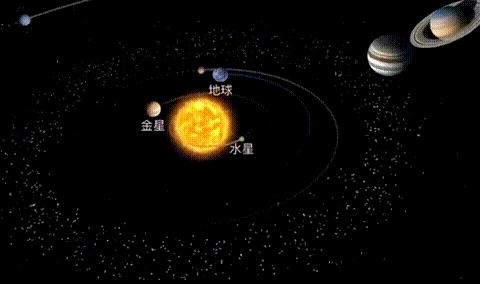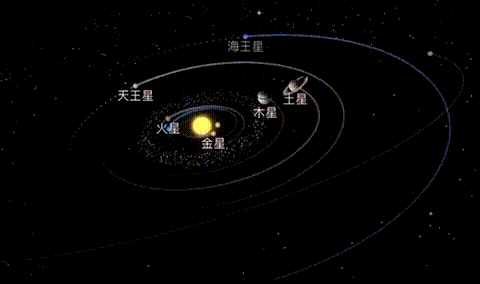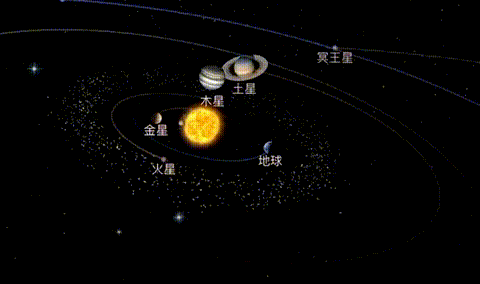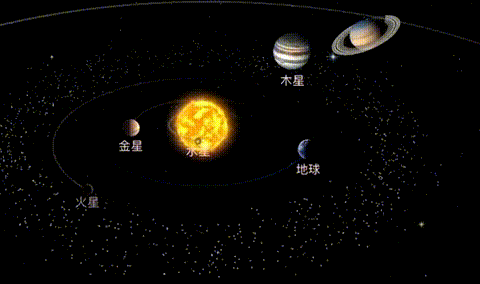
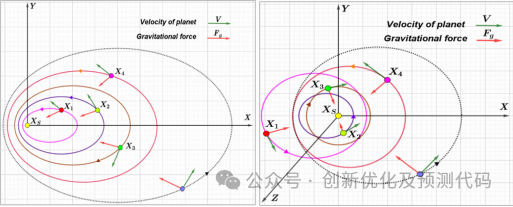
KOA的开普勒优化步骤主要包括初始化行星位置和速度、根据适应度函数评估每个行星的适应度、更新每个行星的位置和速度、更新最佳解（太阳）位置、重复执行更新步骤直到达到停止条件等。这些步骤使得KOA能够在优化过程中更好地探索和利用搜索空间。

构成的KOA-CNN-BiLSTM-Attention多变量回归预测模型的创新性在于以下几点：

KOA算法区别于传统智能算法的创新性：

①受到开普勒行星运动定律的启发：KOA算法受到开普勒行星运动定律的启发，将每个行星的位置作为候选解，并通过随机更新这些候选解来进行优化过程。这种设计使得KOA算法能够更有效地探索和利用搜索空间。

②基于物理学的元启发算法：KOA算法属于物理学的元启发算法，通过模拟行星围绕太阳的运动规律来进行优化。它利用行星的位置、质量、引力和轨道速度等参数来控制候选解的更新过程。这种基于物理学的方法使得KOA算法在全局优化问题上具有更好的可解释性。

③对比其他优化算法的优越性：通过与其他随机优化算法进行对比实验，KOA算法在收敛性和统计数据方面表现出色。实验结果表明，KOA算法在多个基准问题上优于其他比较算法。这表明KOA算法在解决优化问题时具有更高的效果和性能。

优化套用—基于开普勒优化算法（KOA）、卷积神经网络（CNN）和双向长短期记忆网络(BiLSTM)融合注意力机制（SelfAttention）的超前24步多变量时间序列回归预测算法KOA-CNN-LSTM-Attention：

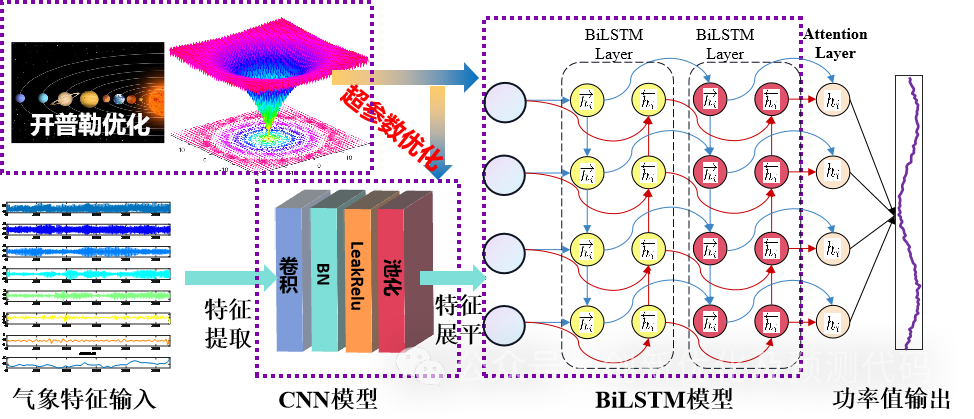
功能：

1、多变量特征输入，单序列变量输出，输入前一天的特征，实现后一天的预测，超前24步预测。

2、通过KOA优化算法优化学习率、卷积核大小、神经元个数，这3个关键参数，以最小MAPE为目标函数。

3、提供损失、RMSE迭代变化极坐标图；网络的特征可视化图；测试对比图；适应度曲线（若首轮精度最高，则适应度曲线为水平直线）。

4、提供MAPE、RMSE、MAE等计算结果展示。

适用领域：风速预测、光伏功率预测、发电功率预测、碳价预测等多种应用。

数据集格式：

前一天18个气象特征，采样时间为24小时，输出为第二天的24小时的功率出力，也就是18×24输入，1×24输出，一共有75个这样的样本。

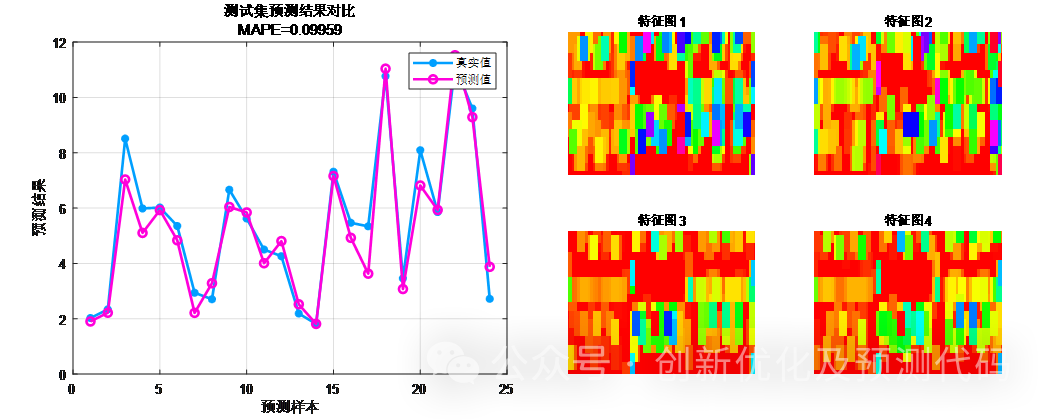
预测值与实际值对比；训练特征可视化：

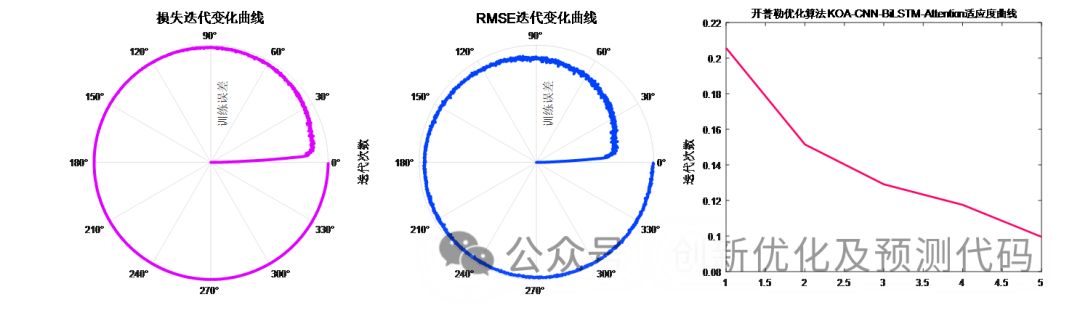
训练误差曲线的极坐标形式（误差由内到外越来越接近0）；适应度曲线（误差逐渐下降）

KOA部分核心代码：

%%  定义Sun_Pos   = zeros(1, dim);  %% 包含迄今为止的最优解的向量，表示太阳Sun_Score = inf;            %% 包含迄今为止的最优分数的标量​%%  控制参数%%Tc = 3;M0 = 0.1;lambda = 15;%% 第1步：初始化过程% 轨道离心率 (e)   orbital = rand(1, SearchAgents_no);                      %% Eq.(4)​ %% 轨道周期 (T) T = abs(randn(1, SearchAgents_no));                      %% Eq.(5)Positions = initialization(SearchAgents_no, dim, ub, lb);%% 初始化行星位置t = 0; %% 函数评估计数器 %%%%---------------------评估-----------------------%%for i = 1:SearchAgents_no    %% 目标函数嵌套    [PL_Fit(i),tsmvalue{i},tnet{i},tinfo{i}] = objectiveFunction(Positions(i,:)');        % 更新迄今为止的最优解    if PL_Fit(i) < Sun_Score      %% 问题为最大化时，请将其更改为>       Sun_Score = PL_Fit(i);     %% 更新迄今为止的最优分数       Sun_Pos = Positions(i,:);  %% 更新迄今为止的最优解       bestPred = tsmvalue{i} ;   %% 更新迄今为止的最准确预测结果       bestNet = tnet{i};       bestInfo  = tinfo{i};    endend​while t < Tmax            %% 终止条件   [Order] = sort(PL_Fit);  %% 对当前种群中的解的适应度值进行排序 %% 函数评估t时的最差适应度值 worstFitness = Order(SearchAgents_no);                  %% Eq.(11) M = M0 * (exp(-lambda * (t / Tmax)));                   %% Eq.(12)​ %% 计算表示太阳与第i个解之间的欧几里得距离R for i = 1:SearchAgents_no    R(i) = 0;    for j = 1:dim       R(i) = R(i) + (Sun_Pos(j) - Positions(i, j))^2;   %% Eq.(7)    end    R(i) = sqrt(R(i)); end %% 太阳和对象i在时间t的质量计算如下： for i = 1:SearchAgents_no    sum = 0;    for k = 1:SearchAgents_no        sum = sum + (PL_Fit(k) - worstFitness);    end    MS(i) = rand * (Sun_Score - worstFitness) / (sum);   %% Eq.(8)    m(i) = (PL_Fit(i) - worstFitness) / (sum);           %% Eq.(9) end  %% 第2步：定义引力（F） % 计算太阳和第i个行星的引力，根据普遍的引力定律： for i = 1:SearchAgents_no    Rnorm(i) = (R(i) - min(R)) / (max(R) - min(R));      %% 归一化的R（Eq.(24)）    MSnorm(i) = (MS(i) - min(MS)) / (max(MS) - min(MS)); %% 归一化的MS    Mnorm(i) = (m(i) - min(m)) / (max(m) - min(m));      %% 归一化的m    Fg(i) = orbital(i) * M * ((MSnorm(i) * Mnorm(i)) / (Rnorm(i) * Rnorm(i) + eps)) + (rand); %% Eq.(6) end

部分图片来源于网络，侵权联系删除！

欢迎感兴趣的小伙伴联系小编获得完整版代码哦~

关注小编会不定期推送高创新型、高质量的学习资料、文章程序代码，为你的科研加油助力!