数据结构与算法：图

news2025/11/1 4:23:24

文章目录

  • 图
      • 1) 概念
        • 有向 vs 无向
        • 度
        • 权
        • 路径
        • 环
        • 图的连通性
      • 2) 图的表示
      • 3) Java 表示
      • 4) DFS
      • 5) BFS
      • 6) 拓扑排序
      • 7) 最短路径
        • Dijkstra
        • Bellman-Ford
        • Floyd-Warshall
      • 8) 最小生成树
        • Prim
        • Kruskal

图

1) 概念

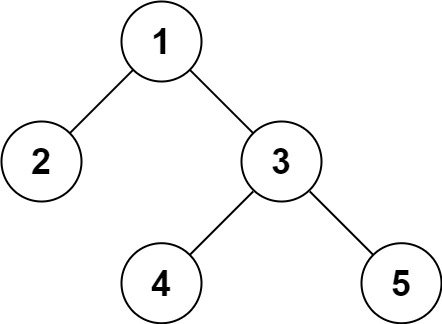
图是由顶点（vertex）和边（edge）组成的数据结构，例如
A
B
C
D

该图有四个顶点：A、B、C、D 以及四条有向边，有向图中，边是单向的

有向 vs 无向

如果是无向图，那么边是双向的，下面是一个无向图的例子
A
B
C
D
度

度是指与该顶点相邻的边的数量
A
B
C
D
E
F

例如上图中

  • A、B、C、E、F 这几个顶点度数为 2
  • D 顶点度数为 4

有向图中，细分为入度和出度，参见下图
A
B
C
D
E
F
  • A (2 out / 0 in)
  • B、C、E (1 out / 1 in)
  • D (2 out / 2 in)
  • F (0 out / 2 in)
权

边可以有权重，代表从源顶点到目标顶点的距离、费用、时间或其他度量。
北京
武汉
广州
上海
800km
1900km
1200km
1050km
700km
路径

路径被定义为从一个顶点到另一个顶点的一系列连续边，例如上图中【北京】到【上海】有多条路径

  • 北京 - 上海
  • 北京 - 武汉 - 上海

路径长度

  • 不考虑权重，长度就是边的数量
  • 考虑权重，一般就是权重累加
环

在有向图中，从一个顶点开始，可以通过若干条有向边返回到该顶点，那么就形成了一个环
A
B
C
D
E
图的连通性

如果两个顶点之间存在路径，则这两个顶点是连通的，所有顶点都连通，则该图被称之为连通图，若子图连通，则称为连通分量
A
B
C
D
E
F
G
H
I
J

2) 图的表示

比如说，下面的图
A
B
C
D

用邻接矩阵可以表示为：

  A B C D
A 0 1 1 0
B 1 0 0 1 
C 1 0 0 1
D 0 1 1 0

用邻接表可以表示为：

A -> B -> C
B -> A -> D
C -> A -> D
D -> B -> C

有向图的例子
A
B
C
D 
  A B C D
A 0 1 1 0
B 0 0 0 1
C 0 0 0 1
D 0 0 0 0

A - B - C
B - D
C - D
D - empty

3) Java 表示

顶点

public class Vertex {
    String name;
    List<Edge> edges;

    // 拓扑排序相关
    int inDegree;
    int status; // 状态 0-未访问 1-访问中 2-访问过，用在拓扑排序

    // dfs, bfs 相关
    boolean visited;

    // 求解最短距离相关
    private static final int INF = Integer.MAX_VALUE;
    int dist = INF;
    Vertex prev = null;

    @Override
    public String toString() {
        return this.name;
    }
}

边

public class Edge {

    Vertex linked;
    int weight;

    public Edge(Vertex linked) {
        this(linked, 1);
    }

    public Edge(Vertex linked, int weight) {
        this.linked = linked;
        this.weight = weight;
    }
}

4) DFS

public class Dfs {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");

        v1.edges = List.of(new Edge(v3), new Edge(v2), new Edge(v6));
        v2.edges = List.of(new Edge(v4));
        v3.edges = List.of(new Edge(v4), new Edge(v6));
        v4.edges = List.of(new Edge(v5));
        v5.edges = List.of();
        v6.edges = List.of(new Edge(v5));

        dfs1(v1);
    }

    private static void dfs2(Vertex v) {
        LinkedList<Vertex> stack = new LinkedList<>();
        stack.push(v);
        while (!stack.isEmpty()) {
            Vertex pop = stack.pop();
            pop.visited = true;
            System.out.println(pop.name);
            for (Edge edge : pop.edges) {
                if (!edge.linked.visited) {
                    stack.push(edge.linked);
                }
            }
        }
    }

    private static void dfs1(Vertex v) {
        v.visited = true;
        System.out.println(v.name);
        for (Edge edge : v.edges) {
            if (!edge.linked.visited) {
                dfs(edge.linked);
            }
        }
    }
}

5) BFS

public class Bfs {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");

        v1.edges = List.of(new Edge(v3), new Edge(v2), new Edge(v6));
        v2.edges = List.of(new Edge(v4));
        v3.edges = List.of(new Edge(v4), new Edge(v6));
        v4.edges = List.of(new Edge(v5));
        v5.edges = List.of();
        v6.edges = List.of(new Edge(v5));

        bfs(v1);
    }

    private static void bfs(Vertex v) {
        LinkedList<Vertex> queue = new LinkedList<>();
        v.visited = true;
        queue.offer(v);
        while (!queue.isEmpty()) {
            Vertex poll = queue.poll();
            System.out.println(poll.name);
            for (Edge edge : poll.edges) {
                if (!edge.linked.visited) {
                    edge.linked.visited = true;
                    queue.offer(edge.linked);
                }
            }
        }
    }
}

6) 拓扑排序
网页基础
Java Web
Java 基础
数据库
Spring框架
微服务框架
实战项目 
public class TopologicalSort {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("网页基础");
        Vertex v2 = new Vertex("Java基础");
        Vertex v3 = new Vertex("JavaWeb");
        Vertex v4 = new Vertex("Spring框架");
        Vertex v5 = new Vertex("微服务框架");
        Vertex v6 = new Vertex("数据库");
        Vertex v7 = new Vertex("实战项目");

        v1.edges = java.util.List.of(new Edge(v3)); // +1
        v2.edges = java.util.List.of(new Edge(v3)); // +1
        v3.edges = java.util.List.of(new Edge(v4));
        v6.edges = java.util.List.of(new Edge(v4));
        v4.edges = java.util.List.of(new Edge(v5));
        v5.edges = java.util.List.of(new Edge(v7));
        v7.edges = java.util.List.of();
        List<Vertex> graph = java.util.List.of(v1,v2,v3,v4,v5,v6,v7);
        for (Vertex vertex : graph) {
            for (Edge edge : vertex.edges) {
                edge.linked.inDegree += 1;
            }
        }

        List<Vertex> result = new ArrayList<>();
        Stack<Vertex> stack = new Stack<>();
        for (Vertex vertex : graph) {
            if(vertex.inDegree == 0 ){
                stack.push(vertex);
            }
        }
        while(!stack.isEmpty()){
            Vertex pop = stack.pop();
            result.add(pop);
            for (Edge edge : pop.edges) {
                edge.linked.inDegree--;
                if(edge.linked.inDegree == 0 && !edge.linked.visited){
                    stack.add(edge.linked);
                    edge.linked.visited = true;
                }
            }
        }
        if(result.size() != graph.size()){
            System.out.println("发现环");
        }
        for (Vertex vertex : result) {
            System.out.println(vertex);
        }

    }

7) 最短路径

Dijkstra
7
9
14
9
2
15
11
6
1
2
3
4
5
6

算法描述：

  1. 将所有顶点标记为未访问。创建一个未访问顶点的集合。
  2. 为每个顶点分配一个临时距离值
    • 对于我们的初始顶点，将其设置为零
    • 对于所有其他顶点，将其设置为无穷大。
  3. 每次选择最小临时距离的未访问顶点，作为新的当前顶点
  4. 对于当前顶点，遍历其所有未访问的邻居，并更新它们的临时距离为更小
    • 例如，1->6 的距离是 14，而1->3->6 的距离是11。这时将距离更新为 11
    • 否则，将保留上次距离值
  5. 当前顶点的邻居处理完成后，把它从未访问集合中删除
public class Dijkstra {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");

        v1.edges = List.of(new Edge(v3, 9), new Edge(v2, 7), new Edge(v6, 14));
        v2.edges = List.of(new Edge(v4, 15));
        v3.edges = List.of(new Edge(v4, 11), new Edge(v6, 2));
        v4.edges = List.of(new Edge(v5, 6));
        v5.edges = List.of();
        v6.edges = List.of(new Edge(v5, 9));

        List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6);

        dijkstra(graph, v1);
    }

    private static void dijkstra(List<Vertex> graph, Vertex source) {
        ArrayList<Vertex> list = new ArrayList<>(graph);
        source.dist = 0;

        while (!list.isEmpty()) {
            // 3. 选取当前顶点
            Vertex curr = chooseMinDistVertex(list);
            // 4. 更新当前顶点邻居距离
            updateNeighboursDist(curr, list);
            // 5. 移除当前顶点
            list.remove(curr);
        }

        for (Vertex v : graph) {
            System.out.println(v.name + " " + v.dist);
        }
    }

    private static void updateNeighboursDist(Vertex curr, ArrayList<Vertex> list) {
        for (Edge edge : curr.edges) {
            Vertex n = edge.linked;
            if (list.contains(n)) {
                int dist = curr.dist + edge.weight;
                if (dist < n.dist) {
                    n.dist = dist;
                }
            }
        }
    }

    private static Vertex chooseMinDistVertex(ArrayList<Vertex> list) {
        Vertex min = list.get(0);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i).dist < min.dist) {
                min = list.get(i);
            }
        }
        return min;
    }

}

改进 - 优先级队列

  1. 创建一个优先级队列，放入所有顶点（队列大小会达到边的数量）
  2. 为每个顶点分配一个临时距离值
    • 对于我们的初始顶点，将其设置为零
    • 对于所有其他顶点，将其设置为无穷大。
  3. 每次选择最小临时距离的未访问顶点，作为新的当前顶点
  4. 对于当前顶点，遍历其所有未访问的邻居，并更新它们的临时距离为更小，若距离更新需加入队列
    • 例如，1->6 的距离是 14，而1->3->6 的距离是11。这时将距离更新为 11
    • 否则，将保留上次距离值
  5. 当前顶点的邻居处理完成后，把它从队列中删除
public class DijkstraPriorityQueue {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");

        v1.edges = List.of(new Edge(v3, 9), new Edge(v2, 7), new Edge(v6, 14));
        v2.edges = List.of(new Edge(v4, 15));
        v3.edges = List.of(new Edge(v4, 11), new Edge(v6, 2));
        v4.edges = List.of(new Edge(v5, 6));
        v5.edges = List.of();
        v6.edges = List.of(new Edge(v5, 9));

        List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6);

        dijkstra(graph, v1);
    }

    private static void dijkstra(List<Vertex> graph, Vertex source) {
        PriorityQueue<Vertex> queue = new PriorityQueue<>(Comparator.comparingInt(v -> v.dist));
        source.dist = 0;
        for (Vertex v : graph) {
            queue.offer(v);
        }

        while (!queue.isEmpty()) {
            System.out.println(queue);
            // 3. 选取当前顶点
            Vertex curr = queue.poll();
            // 4. 更新当前顶点邻居距离
            if(!curr.visited) {
                updateNeighboursDist(curr, queue);
                curr.visited = true;
            }
            // 5. 移除当前顶点
        }

        for (Vertex v : graph) {
            System.out.println(v.name + " " + v.dist + " " + (v.prev != null ? v.prev.name : "null"));
        }
    }

    private static void updateNeighboursDist(Vertex curr, PriorityQueue<Vertex> queue) {
        for (Edge edge : curr.edges) {
            Vertex n = edge.linked;
            if (!n.visited) {
                int dist = curr.dist + edge.weight;
                if (dist < n.dist) {
                    n.dist = dist;
                    n.prev = curr;
                    queue.remove(n); // 先删除再添加才能改变优先级
                    queue.offer(n);
                }
            }
        }
    }

}

问题

2
1
-2
1
v1
v2
v3
v4

按照 Dijkstra 算法，得出

  • v1 -> v2 最短距离2
  • v1 -> v3 最短距离1
  • v1 -> v4 最短距离2

事实应当是

  • v1 -> v2 最短距离2
  • v1 -> v3 最短距离0
  • v1 -> v4 最短距离1
Bellman-Ford
public class BellmanFord {
    public static void main(String[] args) {
        // 正常情况
        /*Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");

        v1.edges = List.of(new Edge(v3, 9), new Edge(v2, 7), new Edge(v6, 14));
        v2.edges = List.of(new Edge(v4, 15));
        v3.edges = List.of(new Edge(v4, 11), new Edge(v6, 2));
        v4.edges = List.of(new Edge(v5, 6));
        v5.edges = List.of();
        v6.edges = List.of(new Edge(v5, 9));

        List<Vertex> graph = List.of(v4, v5, v6, v1, v2, v3);*/

        // 负边情况
        /*Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");

        v1.edges = List.of(new Edge(v2, 2), new Edge(v3, 1));
        v2.edges = List.of(new Edge(v3, -2));
        v3.edges = List.of(new Edge(v4, 1));
        v4.edges = List.of();
        List<Vertex> graph = List.of(v1, v2, v3, v4);*/

        // 负环情况
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");

        v1.edges = List.of(new Edge(v2, 2));
        v2.edges = List.of(new Edge(v3, -4));
        v3.edges = List.of(new Edge(v4, 1), new Edge(v1, 1));
        v4.edges = List.of();
        List<Vertex> graph = List.of(v1, v2, v3, v4);

        bellmanFord(graph, v1);
    }

    private static void bellmanFord(List<Vertex> graph, Vertex source) {
        source.dist = 0;
        int size = graph.size();
        // 1. 进行 顶点个数 - 1 轮处理
        for (int i = 0; i < size - 1; i++) {
            // 2. 遍历所有的边
            for (Vertex s : graph) {
                for (Edge edge : s.edges) {
                    // 3. 处理每一条边
                    Vertex e = edge.linked;
                    if (s.dist != Integer.MAX_VALUE && s.dist + edge.weight < e.dist) {
                        e.dist = s.dist + edge.weight;
                        e.prev = s;
                    }
                }
            }
        }
        for (Vertex v : graph) {
            System.out.println(v + " " + (v.prev != null ? v.prev.name : "null"));
        }
    }
}

负环

2
-4
1
1
v1
v2
v3
v4

如果在【顶点-1】轮处理完成后，还能继续找到更短距离，表示发现了负环

Floyd-Warshall
-2
4
3
2
-1
v1
v3
v2
v4 
public class FloydWarshall {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");

        v1.edges = List.of(new Edge(v3, -2));
        v2.edges = List.of(new Edge(v1, 4), new Edge(v3, 3));
        v3.edges = List.of(new Edge(v4, 2));
        v4.edges = List.of(new Edge(v2, -1));
        List<Vertex> graph = List.of(v1, v2, v3, v4);

        /*
                直接连通
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   3   ∞
            v3  ∞   ∞   0   2
            v4  ∞   -1  ∞   0

                k=0 借助v1到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   2   ∞
            v3  ∞   ∞   0   2
            v4  ∞   -1  ∞   0

                k=1 借助v2到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   2   ∞
            v3  ∞   ∞   0   2
            v4  3   -1  1   0

                k=2 借助v3到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  0
            v2  4   0   2   4
            v3  ∞   ∞   0   2
            v4  3   -1  1   0

                k=3 借助v4到达其它顶点
                v1  v2  v3  v4
            v1  0   -1   -2  0
            v2  4   0   2   4
            v3  5   1   0   2
            v4  3   -1  1   0
         */
        floydWarshall(graph);
    }

    private static void floydWarshall(List<Vertex> graph){
        int size = graph.size();
        int[][] dist = new int[size][size];
        for (int i = 0; i < size; i++) {  // 初始化
            Vertex vertex = graph.get(i);
            Map<Vertex, Integer> collect = vertex.edges.stream().collect(Collectors.toMap(v -> v.linked, v -> v.weight));
            for (int i1 = 0; i1 < size; i1++) {
                if(i == i1){
                    dist[i][i1] = 0;
                    continue;
            }
                dist[i][i1] = collect.getOrDefault(graph.get(i1),Integer.MAX_VALUE);
        }
        }
        for (int k = 0; k < size; k++) {
            for (int j = 0; j < size; j++) {
                int dist1;
                if((dist1 = dist[j][k]) < Integer.MAX_VALUE){
                    for (int i = 0; i < size; i++) {
                        int dist2;
                        if((dist2 = dist[k][i]) != Integer.MAX_VALUE)
                            dist[j][i] = Integer.min(dist1 + dist2,dist[j][i]);
                    }
                }
            }
        }

        for (int[] ints : dist) {
            for (int anInt : ints) {
                System.out.print(anInt + " ");
            }
            System.out.println();
        }
    }
}

负环

如果在 3 层循环结束后，在 dist 数组的对角线处（i==j 处）发现了负数，表示出现了负环

8) 最小生成树

图的最小生成树是一个子图，它是连通的，包含图中所有的顶点，并且所有边的权重之和最小。在最小生成树中，没有任何一条边可以被其他边替换而使得总权重变小。也就是说，最小生成树是图的所有生成树中，边的权值总和最小的生成树。

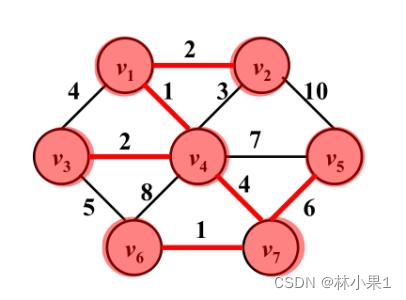
请添加图片描述

解决最小生成树问题的常用算法有Prim算法和Kruskal算法。Prim算法从一个顶点开始，每次都添加一条与当前子图连接的权重最小的边，直到所有顶点都被包含在子图中。Kruskal算法则是从所有的边开始，每次都添加一条当前所有边中权重最小的边，但需要保证添加的边不会形成环，直到所有顶点都被连接。

Prim
public class Prim {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");
        Vertex v7 = new Vertex("v7");

        v1.edges = List.of(new Edge(v2, 2), new Edge(v3, 4), new Edge(v4, 1));
        v2.edges = List.of(new Edge(v1, 2), new Edge(v4, 3), new Edge(v5, 10));
        v3.edges = List.of(new Edge(v1, 4), new Edge(v4, 2), new Edge(v6, 5));
        v4.edges = List.of(new Edge(v1, 1), new Edge(v2, 3), new Edge(v3, 2),
                new Edge(v5, 7), new Edge(v6, 8), new Edge(v7, 4));
        v5.edges = List.of(new Edge(v2, 10), new Edge(v4, 7), new Edge(v7, 6));
        v6.edges = List.of(new Edge(v3, 5), new Edge(v4, 8), new Edge(v7, 1));
        v7.edges = List.of(new Edge(v4, 4), new Edge(v5, 6), new Edge(v6, 1));

        List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6, v7);

        prim(graph, v1);

    }

    static void prim(List<Vertex> graph, Vertex source) {
        ArrayList<Vertex> list = new ArrayList<>(graph);
        source.dist = 0;

        while (!list.isEmpty()) {
            Vertex min = chooseMinDistVertex(list);
            updateNeighboursDist(min);
            list.remove(min);
            min.visited = true;
            System.out.println("---------------");
            for (Vertex v : graph) {
                System.out.println(v);
            }
        }


    }

    private static void updateNeighboursDist(Vertex curr) {
        for (Edge edge : curr.edges) {
            Vertex n = edge.linked;
            if (!n.visited) {
                int dist = edge.weight;
                if (dist < n.dist) {
                    n.dist = dist;
                    n.prev = curr;
                }
            }
        }
    }

    private static Vertex chooseMinDistVertex(ArrayList<Vertex> list) {
        Vertex min = list.get(0);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i).dist < min.dist) {
                min = list.get(i);
            }
        }
        return min;
    }
}
Kruskal
  private static void kruskal(List<Vertex> graph,Vertex v1){
    List<Edge> edges = new ArrayList<>();
    List<Vertex> pre = new ArrayList<>();
    for (Vertex vertex : graph) {
        for (Edge edge : vertex.edges) {
            edges.add(edge);
            pre.add(vertex);
        }
    }
    for (int i = 0; i < edges.size(); i++) {
        Edge minEdge = edges.get(i);
        int min = minEdge.weight;
        for (int j = i + 1 ; j < edges.size(); j++) {
            Edge e = edges.get(j);
            if(minEdge.weight > e.weight){
                edges.set(j,minEdge);
                minEdge = e;
                edges.set(i,e);
                Vertex v = pre.get(i);
                pre.set(i,pre.get(j));
                pre.set(j,v);
            }
        }
    }
    List<Vertex> used = new ArrayList<>();
    for (int i = 0; i < edges.size(); i++) {
        Vertex v = pre.get(i);
        Vertex e = edges.get(i).linked;
        if(!used.contains(v) || !used.contains(e)){
            System.out.println(v.name + " -> " + e.name);
            used.add(v);
            used.add(e);
        }
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1402824.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何搭建MariaDB并实现无公网ip环境远程连接本地数据库

如何搭建MariaDB并实现无公网ip环境远程连接本地数据库

&#x1f308;个人主页: Aileen_0v0 &#x1f525;热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 ​&#x1f4ab;个人格言:“没有罗马,那就自己创造罗马~” 文章目录 1. 配置MariaDB数据库1.1 安装MariaDB数据库1.2 测试局域网内远程连接 2. 内网穿透2.1 创建隧道映射…
阅读更多...
【C++】stack与queue的模拟实现

【C++】stack与queue的模拟实现

&#x1f440;樊梓慕&#xff1a;个人主页 &#x1f3a5;个人专栏&#xff1a;《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》《算法》 &#x1f31d;每一个不曾起舞的日子&#xff0c;都是对生命的辜负 前言 stack与queue的实现比较简…
阅读更多...
Mysql - 定点型(DECIMAL)的使用详解及练习

Mysql - 定点型(DECIMAL)的使用详解及练习

目录 &#x1f436;1. 前言&#xff1a; &#x1f436;2. DECIMAL类型简介 &#x1f436;3. Decimal使用实战 &#x1f96a;#结论1&#xff1a;小数位不足会自动补0 &#x1f96a;#结论2&#xff1a;小数位超出会截断 并按四舍五入处理。 &#x1f96a;#结论3&#xff1…
阅读更多...
代码随想录算法训练营第34天 |1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果

代码随想录算法训练营第34天 |1005.K次取反后最大化的数组和 134. 加油站 135. 分发糖果

1005.K次取反后最大化的数组和 题目链接&#xff1a;1005.K次取反后最大化的数组和 给定一个整数数组 A&#xff0c;我们只能用以下方法修改该数组&#xff1a;我们选择某个索引 i 并将 A[i] 替换为 -A[i]&#xff0c;然后总共重复这个过程 K 次。&#xff08;我们可以多次选…
阅读更多...
【明道云】学习笔记1-了解APaaS

【明道云】学习笔记1-了解APaaS

【背景】 APaaS (Application Platform As A Service) &#xff0c;即应用程序平台即服务&#xff0c;这是基于PaaS&#xff08;平台即服务&#xff09;的一种解决方案&#xff0c;支持应用程序在云端的开发、部署和运行&#xff0c;提供软件开发中的基础工具给用户&#xff0…
阅读更多...
【JavaEE进阶】 Spring Boot⽇志

【JavaEE进阶】 Spring Boot⽇志

文章目录 &#x1f38b;关于日志&#x1f6a9;为什么要学习⽇志&#x1f6a9;⽇志的⽤途&#x1f6a9;日志的简单使用 &#x1f384;打印⽇志&#x1f6a9;程序中得到⽇志对象&#x1f6a9;使⽤⽇志对象打印⽇志 &#x1f38d;⽇志格式的说明&#x1f6a9;⽇志级别的作用&#…
阅读更多...
Java - 深入理解加密解密和签名算法

Java - 深入理解加密解密和签名算法

文章目录 应用的接口安全性问题可能来源加密解密Why保护数据隐私防止未经授权的访问防止数据泄露 对称加密 VS 单向加密 VS 非对称加密一、对称加密二、单向加密&#xff08;哈希加密&#xff09;三、非对称加密 常用的对称加密算法1. AES&#xff08;高级加密标准&#xff09;…
阅读更多...
【Java】学习一门开发语言，从TA的Hello World开始

【Java】学习一门开发语言，从TA的Hello World开始

欢迎来到《小5讲堂》 大家好&#xff0c;我是全栈小5。 这是《Java》序列文章&#xff0c;每篇文章将以博主理解的角度展开讲解&#xff0c; 特别是针对知识点的概念进行叙说&#xff0c;大部分文章将会对这些概念进行实际例子验证&#xff0c;以此达到加深对知识点的理解和掌握…
阅读更多...
第15届蓝桥杯嵌入式省赛准备第二天总结笔记(使用STM32cubeMX创建hal库工程+按键输入)

第15届蓝桥杯嵌入式省赛准备第二天总结笔记(使用STM32cubeMX创建hal库工程+按键输入)

一.查看电路图 按键是使用的PB0,PB1,PB2,PA0四个引脚&#xff0c;然后使用CubeMX配置引脚&#xff0c;4个脚都配置为输入模式和上拉。 程序生成之后把不用的删掉&#xff0c;需要的留下&#xff0c;这里我把函数名改了。 然后写按键扫描读取程序&#xff0c;这里参考的正点原子…
阅读更多...
【Linux】—— 命名管道详解

【Linux】—— 命名管道详解

命名管道是一种在操作系统中用于进程间通信的机制&#xff0c;它允许不同的进程之间通过管道进行数据交换。与匿名管道相比&#xff0c;命名管道具有更多的灵活性和功能。在本博客中&#xff0c;我们将深入探讨命名管道的概念、用途以及如何在编程中使用它们。 目录 &#xff…
阅读更多...
【cucumber】cucumber-reporting生成测试报告

【cucumber】cucumber-reporting生成测试报告

原始的cucumber report 比较粗糙 我们可以通过cucumber-reporting 插件对报告进去优化 在pom.xml里面添加cuccumber-reporting 插件 <!-- 根据 cucumber json文件 美化测试报告--><dependency><groupId>net.masterthought</groupId><artifactId>…
阅读更多...
何为PyTorch？

何为PyTorch？

PyTorch的名字来源于它的功能和设计哲学。"Py"代表Python&#xff0c;因为PyTorch是一个基于Python的深度学习库&#xff0c;它充分利用了Python语言的灵活性和易用性&#xff0c;为开发者提供了简洁而强大的接口。“Torch”则代表其前身—— Torch&#xff0c;这是一…
阅读更多...
瓦片地图游戏开发的底层代码

瓦片地图游戏开发的底层代码

原理&#xff1a; 二维数组存储每个瓦片序号 然后有一个缓冲区存储瓦片图片&#xff0c; 最后连续采样缓冲区&#xff0c;粘贴到屏幕上&#xff0c; 而缓冲区数据随着采样越界再重新更新 #include <graphics.h> #include <stdio.h>// 默认游戏地图 int map[20…
阅读更多...
使用vue-pdf插件加载pdf

使用vue-pdf插件加载pdf

安装&#xff1a; // 安装这个版本&#xff0c;其它版本会有千奇百怪的错&#xff0c;这个版本和4.0.0都是可以的 cnpm install vue-pdf4.2.0// 安装pdfjs-dist cnpm install pdfjs-dist2.5.207 使用&#xff1a; // 我的css样式是pxToRem&#xff0c;友友们使用可能样式会有…
阅读更多...
二叉树题目：二叉树的序列化与反序列化

二叉树题目：二叉树的序列化与反序列化

文章目录 题目标题和出处难度题目描述要求示例数据范围 前言解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题&#xff1a;二叉树的序列化与反序列化 出处&#xff1a;297. 二叉树的序列化与反序列化 难度 8 级 题目描述 要求 序列…
阅读更多...
大数据开发之Scala

大数据开发之Scala

第 1 章&#xff1a;scala入门 1.1 概述 scala将面向对象和函数式编程结合成一种简洁的高级语言 特点 1、scala和java一样属于jvm语言&#xff0c;使用时都需要先编译为class字节码文件&#xff0c;并且scala能够直接调用java的类库 2、scala支持两种编程范式面向对象和函数式…
阅读更多...
MySQL索引优化：深入理解索引下推原理与实践

MySQL索引优化：深入理解索引下推原理与实践

随着MySQL的不断发展和升级&#xff0c;每个版本都为数据库性能和查询优化带来了新的特性。在MySQL 5.6中&#xff0c;引入了一个重要的优化特性——索引下推&#xff08;Index Condition Pushdown&#xff0c;简称ICP&#xff09;。ICP能够在某些查询场景下显著提高查询性能&a…
阅读更多...
JVM系列-3.类的生命周期

JVM系列-3.类的生命周期

&#x1f44f;作者简介&#xff1a;大家好&#xff0c;我是爱吃芝士的土豆倪&#xff0c;24届校招生Java选手&#xff0c;很高兴认识大家&#x1f4d5;系列专栏&#xff1a;Spring原理、JUC原理、Kafka原理、分布式技术原理、数据库技术、JVM原理&#x1f525;如果感觉博主的文…
阅读更多...
想找一个没有中间商的账户，很简单，昂首资本推给你

想找一个没有中间商的账户，很简单，昂首资本推给你

各位投资者都知道&#xff0c;交易的成本决定我们是否盈利&#xff0c;那么有没有一个没有中间商的账户呢&#xff1f;当然有了&#xff0c;昂首资本这就推给你。 在交易的时候&#xff0c;银行为投资者提供兑换业务&#xff0c;并从中收取费用。至于经纪商&#xff0c;它是交…
阅读更多...
爬虫requests+综合练习详解

爬虫requests+综合练习详解

Day2 - 1.requests第一血_哔哩哔哩_bilibili requests作用&#xff1a;模拟浏览器发请求 requests流程&#xff1a;指定url -> 发起请求 -> 获取响应数据 -> 持续化存储 爬取搜狗首页的页面数据 import requests# 指定url url https://sogou.com # 发起请求 resp…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023