（2021|ICLR，扩散先验，VE-SDE，逼真和忠实的权衡）SDEdit：使用随机微分方程引导图像合成和编辑

SDEdit: Guided Image Synthesis and Editing with Stochastic Differential Equations

公和众和号：EDPJ（进 Q 交流群：922230617 或加 VX：CV_EDPJ 进 V 交流群）

0. 摘要

2. 背景：使用随机微分方程进行图像合成

3. 使用 SDEdit 引导图像合成和编辑

5. 实验

0. 摘要

引导图像合成使普通用户能够以最小的努力创建和编辑逼真的照片。关键挑战在于平衡对用户输入（例如，手绘的彩色笔画）的忠实性和合成图像的逼真性。现有基于 GAN 的方法尝试使用条件GAN 或 GAN 反演来实现这种平衡，这些方法具有挑战性，通常需要为各个应用程序提供额外的训练数据或损失函数。为了解决这些问题，我们引入了一种新的图像合成和编辑方法，基于扩散模型生成先验，称为随机微分编辑（Stochastic Differential Editing，SDEdit），通过随机微分方程（stochastic differential equation，SDE）迭代去噪来合成逼真的图像。给定一个带有用户指引（以操纵 RGB 像素的形式）的输入图像，SDEdit 首先向输入添加噪声，然后通过 SDE 先验迭代去噪生成的图像，以增加其逼真性。SDEdit 不需要任务特定的训练或反演，并且可以自然地实现逼真性和忠实性之间的平衡。在人类感知研究中，SDEdit 在多项任务上（包括基于笔画的图像合成和编辑以及图像合成）上优于最先进的基于 GAN 的方法，逼真性得分提高了最多 98.09%，整体满意度得分提高了 91.72%

与条件 GAN 不同，SDEdit 不需要为每个新任务收集训练图像或用户注释；与 GAN 反演不同，SDEdit 不需要设计额外的训练或任务特定的损失函数。SDEdit 仅使用一个在未标记数据上训练的单个预训练 SDE 模型：在以 RGB 像素操纵的形式给定用户指引后，SDEdit 向指引添加高斯噪声，然后运行反向 SDE 来合成图像。

2. 背景：使用随机微分方程进行图像合成

随机微分方程（Stochastic differential equations，SDEs）通过将随机噪声注入动态来推广常微分方程（ordinary differential equations，ODEs）。SDE 的解是一个随时间变化的随机变量（即，随机过程），表示为 x(t) ∈ R^d，其中 t ∈ [0, 1]，表示时间。在图像合成中（Song等，2021），我们假设 x(0) ~ p_0 = p_data 表示来自数据分布的样本，而正向 SDE 通过高斯扩散在 t ∈ (0, 1] 生成 x(t)。给定 x(0)，x(t) 被分布为高斯分布：

其中 σ(t)：[0,1] → [0,∞) 是描述噪声 z 幅度的标量函数，而 α(t)：[0,1] → [0,1] 是表示数据 x(0) 幅度的标量函数。x(t) 的概率密度函数表示为 p_t。

通常考虑两种类型的随机微分方程：方差爆炸型随机微分方程（Variance Exploding SDE，VE-SDE）中对于所有 t 有 α(t)=1，且 σ(1) 为一个大常数，使得 p_1 接近于 N(0, σ^2(1)·I)；而方差保持型随机微分方程（Variance Preserving SDE，VP-SDE）满足对于所有 t 有 α^2(t) + σ^2(t) = 1，且当 t→1 时 α(t)→0，使得 p_1 等于 N(0,I)。VE 和 VP SDE 都会在 t 从 0 到 1 时将数据分布转换为随机高斯噪声。为简便起见，我们在正文的其余部分基于 VE-SDE 进行详细讨论，并在附录 C 中讨论 VP-SDE 过程。尽管在图像领域具有略微不同的形式并在性能上表现不同，但它们共享相同的数学直觉。

使用 VE-SDE 的图像合成。在这些定义下，我们可以将图像合成问题表述为逐渐从带噪声的观测 x(t) 中去除噪声，以恢复 x(0)。这可以通过一个反向 SDE（Anderson, 1982; Song et al., 2021）来实现，该 SDE 从 t=1 到 t=0，基于关于受噪声影响的得分函数 ∇_x log p_t(x) 的知识。例如，VE-SDE 的采样过程由以下（反向）SDE 定义：

其中 -w 是当时间从 t=1 向 t=0 时的维纳过程。如果我们设置初始条件 x(1)∼p_1=N(0, σ^2(1)·I)，那么 x(0) 的解将分布为 p_data。在实践中，可以通过去噪得分匹配（Vincent, 2011）来学习受噪声影响的得分函数。将学到的得分模型表示为 s_θ(x(t), t)，时间 t 的学习目标为：

其中 p_data 是数据分布，而 x(t) 的定义如方程 1 所示。整体训练目标是对每个个体学习目标 L_t 进行加权求和，各种加权程序已在 Ho 等人（2020）；Song 等人（2020；2021）中进行了讨论。

通过参数化的得分模型 s_θ(x(t), t) 来逼近 ∇_x log p_t(x)，SDE 解可以用 Euler-Maruyama 方法进行近似；从 t+Δt 到 t 的更新规则为：

其中 z∼N(0,I)。我们可以选择从 1 到 0 的时间区间的特定离散化，通过初始化 x(0)∼N(0, σ^2(1)·I) 并通过方程 4 进行迭代，生成图像 x(0)。

3. 使用 SDEdit 引导图像合成和编辑

在本节中，我们介绍 SDEdit 并描述如何使用在未标记的图像上预训练的 SDE 模型进行引导式图像合成和编辑。

Setup。用户以操纵 RGB 像素的形式提供一个全分辨率的图像 x^(g)，我们称之为 “引导”。引导可能包含不同层次的细节；高级引导只包含粗略的彩色笔画，中级引导在真实图像上包含彩色笔画，低级引导包含目标图像上的图像块。我们在图 1 中说明了这些引导，非专业人员可以轻松提供。我们的目标是生成具有两个期望的全分辨率图像：

逼真性。图像应该看起来逼真（例如，由人类或神经网络测量）。
忠实性。图像应该与引导 x^(g) 相似（例如，由 L2 距离测量）。

我们注意到，逼真性和忠实性并不是正相关的，因为可以存在逼真但不忠实的图像（例如，一个随机的逼真图像），以及忠实但不逼真的图像（例如，引导本身）。与常规的逆问题不同，我们不假设对测量函数（即，从真实图像到用户创建的 RGB 像素引导的映射）的了解，因此解逆问题的技术（如基于得分模型的解法（Dhariwal & Nichol, 2021; Kawar等，2021）和需要配对数据集的方法（Isola等，2017; Zhu等，2017）在这里不适用。

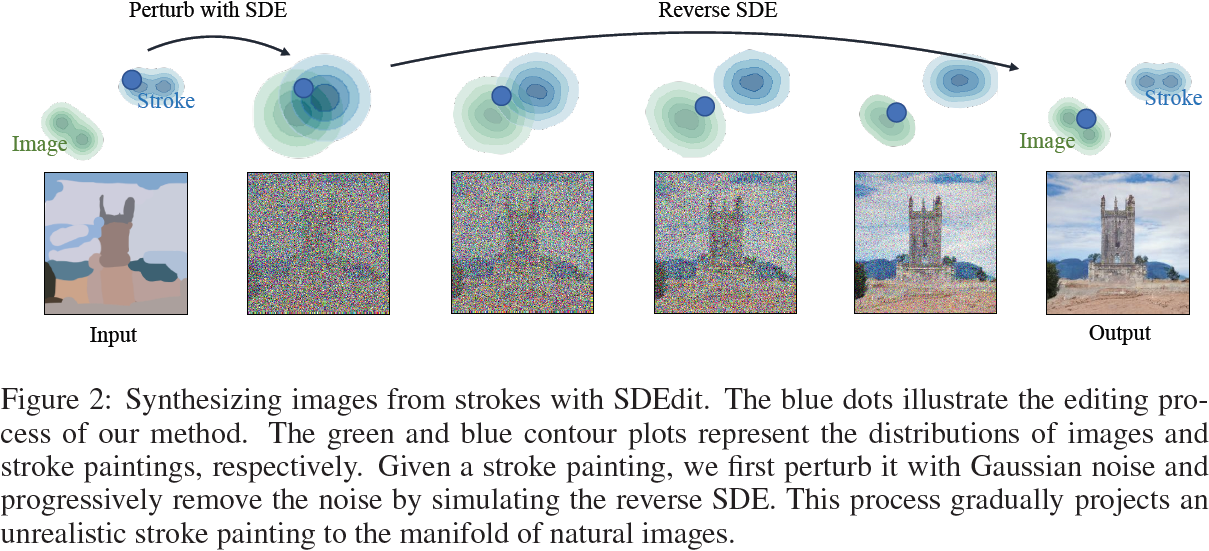
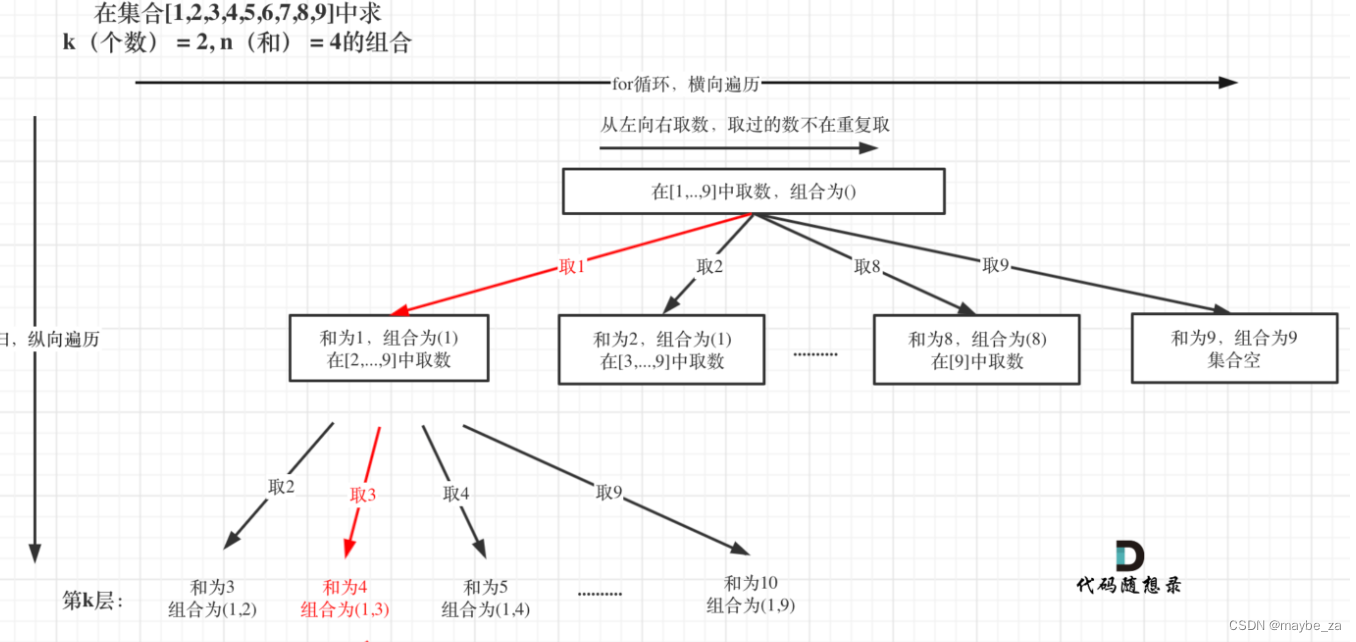
程序。我们的方法 SDEdit 利用了一个事实，即反向 SDE 不仅可以从 t_0 = 1 求解，还可以从任何中间时间 t_0 ∈ (0,1) 求解——这是先前的基于 SDE 的生成模型未研究的方法。我们需要从我们的引导中找到一个适当的初始化，从这个初始化我们可以求解反向 SDE 以获得理想的、逼真的和忠实的图像。对于任何给定的引导 x^(g)，我们定义 SDEdit 过程：从 N(x^(g), σ^2(t_0)·I) 中抽样 x^(g)(t_0)，然后通过迭代方程 4 生成 x(0)。

我们使用 SDEdit(x(g); t_0, θ) 表示上述过程。实质上，SDEdit 选择一个特定的时间 t_0，向引导 x^(g) 添加标准差为 σ^2(t_0) 的高斯噪声，然后解决相应的反向 SDE 在 t = 0 处生成合成的 x(0)。

除了 SDE 求解器采取的离散化步骤外，SDEdit 的关键超参数是 t_0，即我们开始反向 SDE 图像合成过程的时间。接下来，我们描述一个逼真性和忠实性之间的权衡，使我们能够选择合理的 t_0 值。

逼真性和忠实性的权衡。我们注意到，对于经过适当训练的 SDE 模型，当选择不同的 t_0 值时，存在逼真性和忠实性之间的权衡。为了说明这一点，我们关注 LSUN 数据集，并使用高级笔画作为引导来进行基于笔画的图像生成。我们在附录 D.2 中提供实验细节。我们考虑相同的输入对于不同 t_0 ∈ [0,1] 的选择。为了量化逼真性，我们采用神经方法来比较图像分布，例如 Kernel Inception Score（KID; Bi´nkowski 等，2018）。如果合成图像与真实图像之间的 KID 较低，则合成图像是逼真的。对于忠实性，我们测量合成图像与引导 x^(g) 之间的平方 L2 距离。从图 3 中，我们观察到随着 t_0 的增加，逼真性增加但忠实性减少。

逼真性和忠实性之间的权衡也可以从另一个角度解释。如果引导远离任何逼真的图像，那么我们必须容忍至少一定程度的偏离引导（非忠实性），以便生成逼真的图像。这在以下命题中进行了说明。

命题1。假设对于所有 x∈X 和 t∈[0,1]，都有 ||s_θ(x,t)||^2_2 ≤ C。那么对于所有 δ ∈ (0,1)，公式 5 成立的概率至少为 1−δ，

其中 d 是 x^(g) 的维度数。

我们在附录 A 中提供证明。从高层次上看，引导和合成图像之间的差异可以分解为得分和随机高斯噪声的输出；随着 t_0 的增加，两者都会增加，因此差异变得更大。上述命题表明，为了使图像具有高概率的逼真性，我们必须有足够大的 t_0。另一方面，如果 t_0 太大，那么对引导的忠实性将恶化，SDEdit 将产生随机逼真的图像（极端情况是无条件的图像合成）。

选择 t_0。我们注意到，引导的质量可能会影响合成图像的整体质量。对于合理的引导，我们发现 t_0 ∈ [0.3,0.6] 效果良好。然而，如果引导是一个只有白色像素的图像，那么即使是来自模型分布的最接近的 “逼真” 样本也可能相当远，我们必须通过选择较大的 t_0 来在逼真性和忠实性之间进行权衡。在交互式设置中（用户绘制基于草图的引导），我们可以初始化 t_0∈[0.3,0.6]，合成一个候选样本，然后询问用户样本是否应更忠实或更逼真；从用户的回答中，我们可以通过二分搜索获得一个合理的 t_0。在大规模的非交互式设置中（我们给定一组生成的引导），我们可以在随机选择的图像上执行类似的二分搜索，获得 t_0 并随后在同一任务中的所有引导中将 t_0 固定。尽管不同的引导可能潜在地具有不同的最优 t_0，但我们经验上观察到在相同任务中，共享的 t_0 对所有合理引导的效果良好。

详细算法和扩展。我们在算法 1 中呈现了 VE-SDE 的通用算法。由于空间限制，我们在附录 C 中描述了 VP-SDE 的详细算法。实质上，该算法是用于解决 SDEdit(x(g); t_0, θ) 的 Euler-Maruyama 方法。对于我们希望使合成图像的某些部分与引导相同的情况，我们还可以引入一个额外的通道，用于掩蔽我们不希望编辑的图像部分。这是对主文中提到的 SDEdit 过程的轻微修改，我们在附录 C.2 中详细讨论了这些细节。