目录

一.前言

二.选择排序

2.1 堆排序

2.2选择排序

2.2.1 基本思想

2.2.2直接选择排序

三.结语

---

一.前言

本文给大家带来的是选择排序，其中选择排序中的堆排序在之前我们已经有过详解所以本次主要是对比排序性能，感兴趣的友友可移步观看堆排：https://mp.csdn.net/mp_blog/creation/editor/133394741

码字不易，希望大家多多支持我呀！（三连＋关注，你是我滴神！）

二.选择排序

2.1 堆排序

堆排序是值利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆，排降序要建小堆。

堆排序具体详解可以参考这篇文章：https://mp.csdn.net/mp_blog/creation/editor/133394741

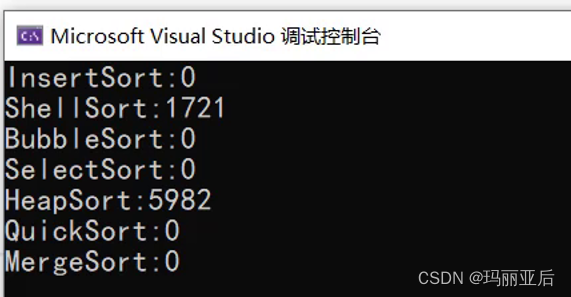
我们这里就先来测试一下堆排序与希尔的效率比较。

堆排序代码：

void AdjustDown(int* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 找出小的那个孩子
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child;
		}

		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			// 继续往下调整
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int n)
{
	// 向下调整建堆
	// O(N)
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}

	// O(N*logN)
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		--end;
	}
}

 这是通过生成100000个随机值测试用的代码片段。

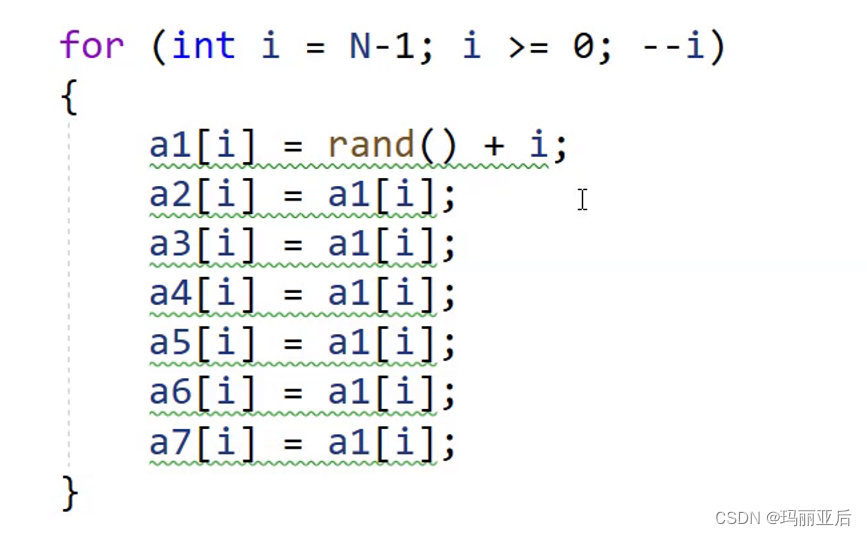
void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i <N; i++)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}

	int begin1 = clock();
	//InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin7 = clock();
	//BubbleSort(a7, N);
	int end7 = clock();

	int begin3 = clock();
	//SelectSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	HeapSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	//QuickSort(a5, 0, N - 1);
	int end5 = clock();

	int begin6 = clock();
	//MergeSort(a6, N);
	int end6 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("BubbleSort:%d\n", end7 - begin7);

	printf("SelectSort:%d\n", end3 - begin3);
	printf("HeapSort:%d\n", end4 - begin4);
	printf("QuickSort:%d\n", end5 - begin5);
	printf("MergeSort:%d\n", end6 - begin6);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

int main()
{
	TestOP();
	//TestBubbleSort();
	//TestHeapSort();
	//TestSelectSort();

	return 0;
}

测试完发现两者算法效率差不多

但是这里面是有一个前提的，就是里面很多数都是重复的，rand函数最多只能产生3万个不同的随机数。当我们追加数字到1亿个时：

堆排序还是会占有优势的。

而在逆序或顺序的情况下，希尔的效率会更高

for (int i = N-1; i >= 0; --i)
	{
		a1[i] = i;
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}

2.2选择排序

2.2.1 基本思想

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

2.2.2直接选择排序

• 在元素集合arr[i]--arr[n-1] 中选择关键码最大（小）的数据元素
• 若它不是这组元素中的最后一个（第一个）元素，则将它与这组元素中的最后一个（第一个）元素交换
• 在剩余的arr[i]--arr[n-2](arr[i+1]--arr[n-1])集合中，重复上述步骤，直到集合剩余1个元素

这是正常版本，下面我们来搞一个优化版，遍历一次来选出最小和最大的。把最小放在左边，最大放在右边。

老规矩先实现单趟代码：走完一遍后标记好最大和最小

void SelectSort(int* a, int n)
{
	//单趟排序
	int maxi = 0;
	int mini = 0;
	for (int i = 1; i < n; i++)
	{
		//在单趟里找出最大最小两个数
		if (a[i] > a[maxi])
		{
			maxi = i;
		}
		if (a[i] < a[mini])
		{
			mini = i;
		}
	}

}

void SelectSort(int* a, int n)
{
	//整体排序与交换
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		//单趟排序
		int maxi = begin;
		int mini = begin;
		for (int i = begin+1; i <=end; i++)
		{
			//在单趟里找出最大最小两个数
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		Swap(&a[end], &a[maxi]);

		begin++;
		end--;
	}
}

走完单趟找出最大值与最小值的时候就开始进行交换，按最小值放右边，最大值放左边的原则。

这里我们统一把最左边设成begin，最右边设置成end。

而整体排序的核心就在于begin与end的变化，在我们的for循环里i的范围是由begin与end来控制的，这代表我们从[begin,end]里寻找最大与最小值

当把该趟的最大最小放置在两侧后，对排序范围进行缩减，通过begin++与end--的方式圈定排序范围，那么我们的下一次单趟范围就在[begin+1,end-1]之间寻找最大与最小，再放置在两侧（最小在begin+1处，最大在end-1处）。

就这样以此类推，两侧就会开始形成序列达到排序的效果。

但这样还不够完整，经过调试我们发现还无法排序，因为还有一个小bug

最开始我们是mini与begin交换即9与1交换，后面按理应该是end与maxi交换，但此时因为9与1交换导致原本指向最大9的maxi不再指向9，而是交换过来的1，导致最后一步是3与1进行交换，所以才会无法排序。

void SelectSort(int* a, int n)
{
	//整体排序与交换
	int begin = 0;
	int end = n - 1;
	while (begin < end)
	{
		//单趟排序
		int maxi = begin;
		int mini = begin;
		for (int i = begin+1; i <=end; i++)
		{
			//在单趟里找出最大最小两个数
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		Swap(&a[begin], &a[mini]);
		if (maxi == begin)
		{
			maxi = mini;
		}
		Swap(&a[end], &a[maxi]);

		begin++;
		end--;
	}
}

所以我们添加一步判断，如果maxi与begin是重合的情况下，在mini与begin交换后重新把指向最大值的mini赋值给maxi即可。

时间复杂度：

第一次是n个数中找2个数，后面是n-2,n-4.....1等差数列，所以时间复杂度为O(N^2)

下面我们来看一下选择与各个排序之间效率高低

在1万个数据中选择排序甚至比不上冒泡排序

那我们再试试有大量重复数据的情况

在重复数据多的情况下，选择还是优于冒泡的。

三.结语

本文的选择排序中也许直接选择排序并没有其他排序那么惊艳甚至会有时被冒泡压上一筹，但它还是有自己的闪光点的，其次是堆排序，在排序效率上与希尔差不多，个别情况也会比希尔高效，这是目前学习过程不容小觑的一类排序算法。因为本文只给了堆排的效率演示具体详解还请友友们移步我之前的文章重新认识一下堆排序~最后感谢大家的观看，友友们能够学习到新的知识是额滴荣幸，期待我们下次相见~