1.使用Git下载vcpkg仓库（下载比较慢，个人比较喜欢打开下面网址然后用迅雷下载，速度飞快）
git clone "https://github.com/Microsoft/vcpkg.git"
2.下载好之后解压打开文件夹，双击bootstrap-vcpkg.bat文件，如果成功的话会在文件夹里生成一个vcpkg.exe文件。（可能会出现窗口闪退导致没有生成exe文件，开启科学上网就可以解决）
3.到这里vcpkg其实就安装完成了，使用vcpkg来安装库的流程如下：
- 在vcpkg所在的文件夹按住shift然后单击鼠标右键打开shell窗口
- 安装集成工具
.\vcpkg.exe integrate install - 生成配置文件
.\vcpkg integrate project
- 下载所需要的第三方库（以gflags为例）
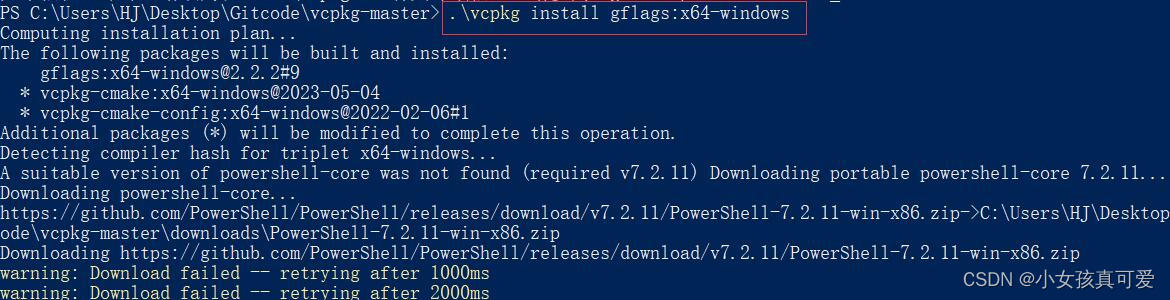在下载库之前它会先下载一个powershell的压缩包，但是这个压缩包下载的非常慢，所以建议复制对应的网址，使用迅雷下载（网址就是图片中https://github........这一大段）
下载完成之后放到vcpkg文件夹下面的downloads文件夹里，然后再重新执行第4步的命令。
- 下载完成之后再重新生成配置文件：
.\vcpkg.exe integrate project
复制这段内容，然后打开visualstudio的项目终端，然后粘贴回车就OK了
