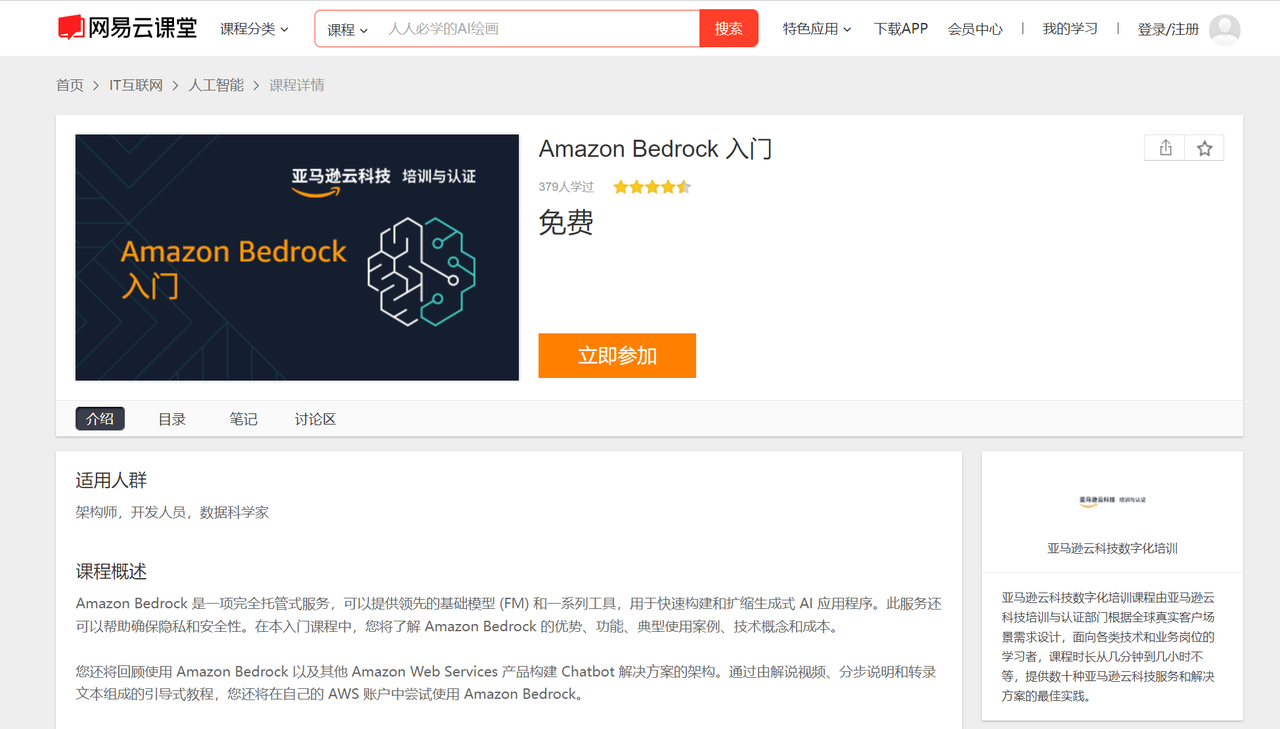
排序算法总结表:
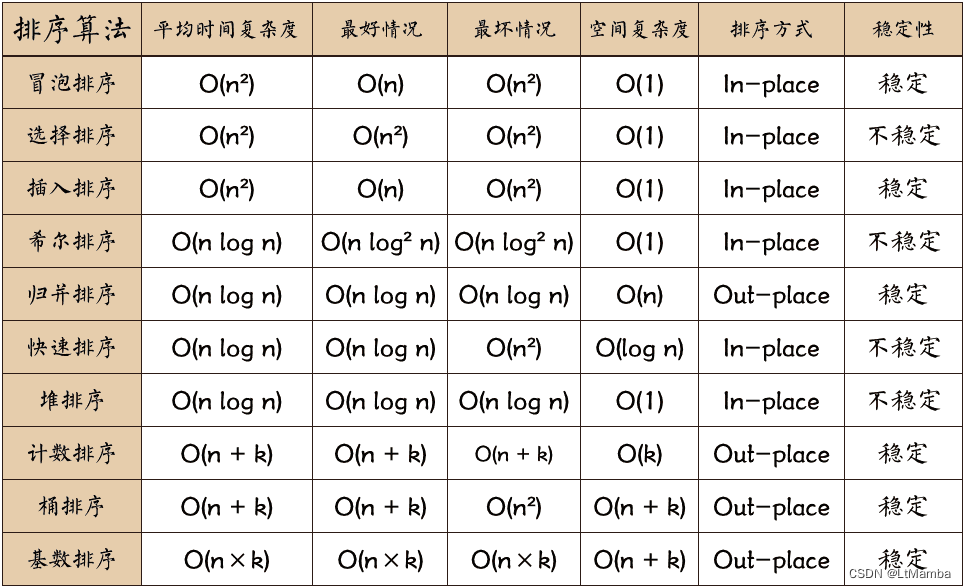
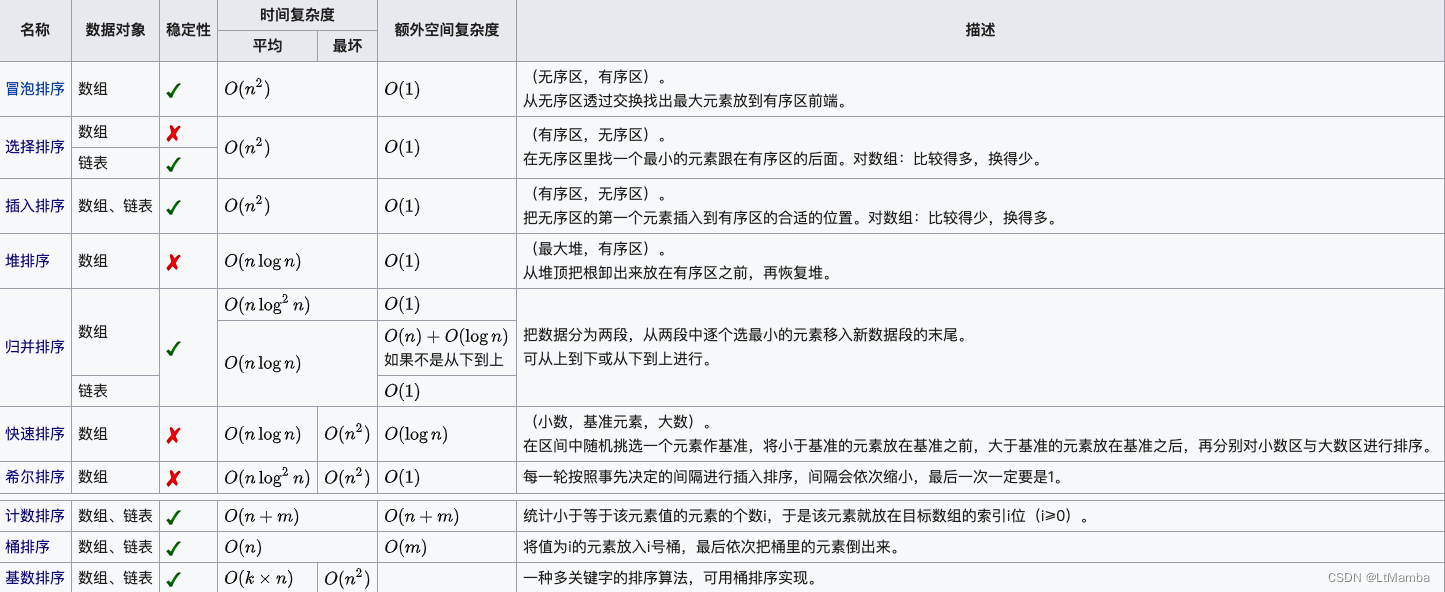
1. In-place 和 Out-place 含义
参考链接
- in-place 占用常数内存,不占用额外内存
假如问题规模是n,在解决问题过程中,只开辟了常数量的空间,与n无关,这是原址操作,就是In-place。
例 :
在冒泡排序中,为了将arr排序,借用了一个temp的临时变量,开辟了一个临时空间,这个空间是常数量,这就是in-place。 - out-place 占用额外内存
如果开辟的辅助空间与问题规模有关,则是out-place。
假设你排序时把数组中的数按顺序放入了一个新的数组,我就开了一个n规模大小的数组,这个就与数据规模有关。
2. 稳定 / 不稳定区别 及 意义
2.1 稳定性的定义
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,ri = rj,且 ri 在 rj 之前,而在排序后的序列中,ri 仍在 rj 之前,则称这种排序算法是稳定的;否则称为不稳定的。
2.2 需要考虑稳定性的场景举例
排序算法的「稳定性」有何意义?这个还是要分应用场景来看,很多使用情况下,并没有什么实质的意义,而在有些情况下却有很重要的意义。
如放在大数据云计算的条件下它的稳定性非常重要。
- 举个例子来说,对淘宝网的商品进行排序,按照销量,价格等条件进行排序,它的数据服务器中的数据非常多,因此,当时用一个稳定性效果不好的排序算法,如堆排序、shell 排序,当遇到最坏情形,会使得排序的效果非常差,严重影响服务器的性能,影响到用户的体验。
3. 时间复杂度
3.1 时间复杂度相关概念
3.1.1 了解什么是对数 logN
参考链接 – 对数,指数,logN
在最简单的层面,对数解答以下问题:
多少个既定的数相乘会等于另一个数?
例子:多少个 2 相乘会等于 8?
正常答案:2 × 2 × 2 = 8,所以需要把 3 个 2 相乘来得到 8
对数答案:对数是 3
即 我们这样写"3个2相乘的积为8": log2(8) = 3
3.1.2 归并排序的时间复杂度 nlogn 是如何推导的
参考链接 – 快速排序和归并排序的时间复杂度分析
假设我们需要对一个包含 n 个数的序列使用归并排序,并且使用的是递归的实现方式,那么过程如下:
递归的第 1 层,将n个数划分为 2 个子区间,每个子区间的数字个数为 n/2;
递归的第 2 层,将n个数划分为 4 个子区间,每个子区间的数字个数为 n/4;
递归的第 3 层,将n个数划分为 8 个子区间,每个子区间的数字个数为 n/8;
......
递归的第logn层,将n个数划分为 n 个子区间,每个子区间的数字个数为 1;
- 解释这里为什么是 logn 层(我是菜鸡,我刚开始就不理解):
假设 最后一层为第 h 层:
已知第 3 层, 将 n 个数划分为 8 个子区间。3 = log8
故 h = logn
我们知道,归并排序的过程中,需要对当前区间进行对半划分,直到区间的长度为 1。也就是说,每一层的子区间,长度都是上一层的 1/2。这也就意味着,当划分到第 logn 层的时候,子区间的长度就是 1 了。而归并排序的 merge 操作,则是从最底层开始(子区间为 1 的层),对相邻的两个子区间进行合并,过程如下:
在第 logn 层(最底层),每个子区间的长度为 1,共 n 个子区间,每相邻两个子区间进行合并,总共合并 n/2 次。n 个数字都会被遍历一次,所有这一层的总时间复杂度为 O(n);
......
在第二层,每个子区间长度为 n/4,总共有 4 个子区间,每相邻两个子区间进行合并,总共合并 2 次。n 个数字都会被遍历一次,所以这一层的总时间复杂度为 O(n);
在第一层,每个子区间长度为 n/2,总共有 2 个子区间,只需要合并一次。n 个数字都会被遍历一次,所以这一层的总时间复杂度为 O(n);
通过上面的过程我们可以发现,对于每一层来说,在合并所有子区间的过程中,n 个元素都会被操作一次,所以每一层的时间复杂度都是 O(n)。而之前我们说过,归并排序划分子区间,将子区间划分为只剩 1 个元素,需要划分logn次。每一层的时间复杂度为 O(n),共有 logn 层,所以归并排序的时间复杂度就是 O(nlogn)。
3.2 时间复杂度排序
| 执行次数函数举例 | 阶 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n2+2n+1 | O(n2) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n3+2n2+3n+4 | O(n3) | 立方阶 |
| 2n | O(2n) | 指数阶 |
注意,经常将 log2n(以2为底的对数)简写成 logn
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
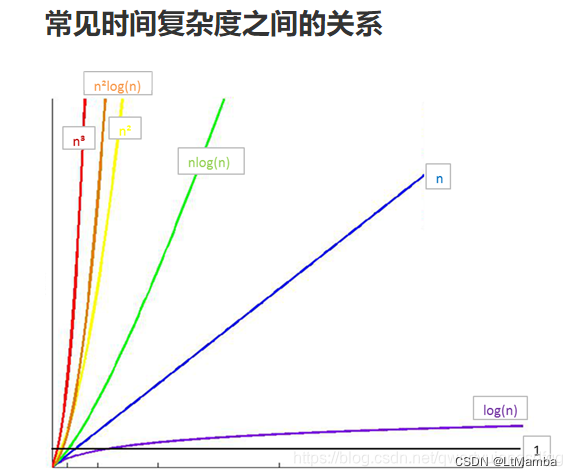
例:
实现相同目的的两个算法时间复杂度为:
算法1:O1(n) = n
算法2:O2(n) = logn
若 n = 4;
故时间复杂度 O1(n) = 4 > O2(n) = log4 = log2^4 = 2,故 O2 更优。
4. 排序算法示例
参考链接–菜鸟教程