【现代密码学基础】详解完美安全与不可区分安全

news2025/1/13 17:31:59

一. 介绍

二. 不可区分性试验

三. 不可区分性与完美安全

四. 例题

五. 小结

一. 介绍

敌手完美不可区分，英文写做perfect adversarial indistinguishability，其中adversarial经常被省略不写，在密码学的论文中经常被简称为IND安全。

完美不可区分与香农的完美安全是类似的。该定义来源于一个被动窃听的敌手试验：给敌手一个密文，然后让敌手猜测明文来源于可能得两个中的哪一个。这个过程其实也可以用计算安全来衡量。

二. 不可区分性试验

敌手A首先随意选择两个明文，如下：

$m_0,m_1\in M$

接着借助Gen算法产生密钥k，利用该密钥对其中的一个明文进行加密。当然此过程明文的选择需要相等的概率。

接着将该密文给敌手A，让他猜测哪一个明文被加密了。如果猜对了，则认为敌手A成功了。

如果敌手成功的概率不会好于1/2，那么认为该加密方案时完美不可区分的。其实，对于任意的加密方案，敌手都可以采用随机均匀的方法进行猜测，这个时候成功的概率即为1/2，不可区分性要求敌手的攻击策略不会优于随机猜测。

注意此处的不可区分性并没有限制敌手的计算能力（computational power）。

将加密方案形式化表达为：

$\Pi=(Gen,Enc,Dec)$

将消息空间表示为M，令A代表敌手，可以抽象成一个确定性的算法，由此可将如上的试验定义为：

$PrivK_{A,\Pi}^{eav}$

试验的具体步骤如下：

注意区分敌手A输出1，代表m1.

试验输出1，代表敌手猜测成功，两者是完全不一样的。

三. 不可区分性与完美安全

在不可区分性试验中，当敌手A随机猜测时，那么他成功的概率就是1/2.完美不可区分性则要求敌手A没有更好的其他策略了。

将以上的过程总结为形式化的定义，如下：

当一个方案是完美不可区分时，那么它也是完美安全的。两者可以互推。

四. 例题

假定某维吉尼亚密码（Vigenere cipher）的明文空间是双子母串。密钥周期可能是1也可能是2，两者均匀选择，如下：

$T=\lbrace 1,2\rbrace$

请证明该维吉尼亚密码不是完美不可区分的。

解：

利用 $\Pi$ 代表该维吉尼亚密码，要想证明该密码方案不是完美不可区分的，其本质则是证明不可区分性试验输出1的概率大于1/2，如下：

接下来我们来详细解释该实验如何展开。

让敌手A执行如下步骤：

第一步：输出两个明文，如下：

$m_0=aa\quad m_1=ab$

在收到挑战密文c后，如下：

$c=c_1c_2$

分成两种情况，敌手输出不同的值：如果发现c1=c2，那么输出0；否则输出1

接下来计算该实验成功的概率可能有些繁琐，但是思想是很直接的。计算如下：

第一个等号：将试验成功分成两种不同的情况，对应两个条件概率

第二个等号：试验成功则是敌手输出的b和实际选择的b相同

以上b代表到底选择哪个明文，当然要求此过程明文的选择是均匀随机比特串。

当敌手输出0时，说明两个密文字母相等。此时b=0，明文m0=aa，也就是c1=c2.出现此种现象有两种可能性：

当密钥的周期为1时，对应的概率为1/2

当密钥的周期为2时，且第一个密钥和第二个密钥相等的概率可计算为：

$\frac{1}{2}\frac{1}{26}$

由此可计算当b=0时，敌手A输出0的概率为：

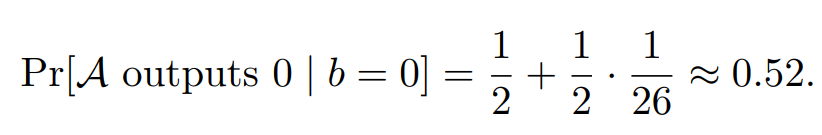
当b=1时，如果要求c1=c2，也就是敌手依旧输出0，由于明文字母是不一样的，所以要求此时的密钥周期必定为2，此时只有一种情况可以实现，所以可以计算为：

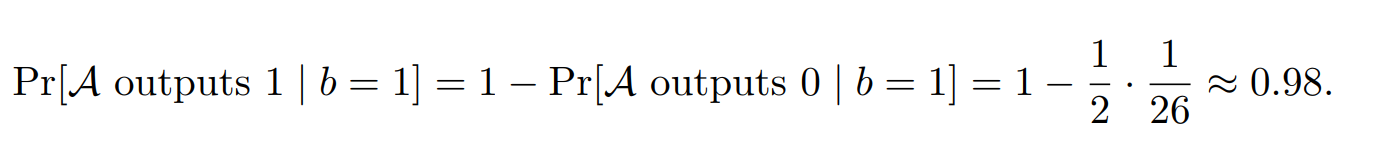
第一个等号：从互补的情况开始思考

第二个等号：1/2代表密钥周期为2，1/26代表：26(1/26)(1/26)

将两者进行合并可得：

很显然该方案不是完美不可区分的。

五. 小结

密码学可分为密码编码学和密码分析学。前者研究如何编解码信息，实现网络安全通信与传输；后者研究如何破译密码或其实现，寻找传输的薄弱环节，二者对立统一、相互促进.

密码编码学

密码编码学主要研究解决信息安全中的机密性、数据完整性、认证、身份识别、可控性及不可抵赖性等问题中的一个或几个。按照加密方式，密码体制可分为对称加密和非对称加密。前者用同一密钥加解密信息，密钥通常需要通过安全的方式分配给通信双方；后者用不同的密钥加解密信息,可将其中一项密钥作为公钥公开，仅将私钥妥善保管即可实现安全通信。

作为密码编码学的重要组成部分，密码算法的安全性和算法设计至关重要。对密码算法的安全性要求主要包括计算安全性、可证明安全性、无条件安全性等，其侧重点有所不同，主要特征如下:

(１)计算安全性：

指用目前算力无法在规定时间内攻破密码算法来说明密码体制的安全性。虽然目前没有被证明计算安全的密码算法，但其可操作性强使得计算安全性成为常用的密码算法评价标准。然而，计算安全性仅说明密码算法的安全性和可计算问题相关,无法证明密码算法绝对安全

(２)可证明安全性：

指用多项式规约技术形式化证明密码体制的安全性。它通过有效的转化将对密码算法的攻击规约为可计算问题的求解。

(３)无条件安全性：

指攻击者在计算资源无限的情况下，密码算法也无法被攻破。密码算法设计的基本原则是加密算法应有不可预测性，主要体现在:１)密码算法需要有较高的线性复杂度，即仅依据密文信息，攻击者很难用统计学方法分析明密文间的关系，从而重现加解密过程;２)加解密流程应足够“混乱”和“扩散”,即通过扩散处理使得加密元素之间相互影响,输入中任何微小的变化都会造成输出改变.