结构体内存对齐(面试重点)

news2025/1/14 0:50:00

结构体内存对齐

    • 1. 结构体类型的声明
      • 1.1 结构体的概念
        • 1.1.1 结构的声明
        • 1.1.2 结构体变量的创建和初始化
      • 1.2 结构的特殊声明
      • 1.3 结构的自引用
    • 2. 结构体内存对齐
      • 2.1 对齐规则
        • 2.1.1 练习1:
        • 2.1.2 练习2:
        • 2.1.3 练习3:
        • 2.1.4 练习4:
      • 2.2 offsetof宏的使用
      • 2.3 为什么存在内存对齐?
      • 2.4 修改默认对齐数
    • 3. 结构体传参
      • 3.1 代码一
      • 3.2 代码二

1. 结构体类型的声明

1.1 结构体的概念

结构是⼀些值的集合，这些值称为成员变量。结构的每个成员可以是不同类型的变量。

1.1.1 结构的声明
struct tag
{
	member-list;
}variable-list;

例如描述⼀个学⽣：

struct Stu
{
	char name[20];//名字
	int age;//年龄
	char sex[5];//性别
	char id[20];//学号
}; //分号不能丢
1.1.2 结构体变量的创建和初始化
#include <stdio.h>

struct Stu
{
	char name[20];//名字
	int age;//年龄
	char sex[5];//性别
	char id[20];//学号
};

int main()
{
	//按照结构体成员的顺序初始化
	struct Stu s = { "张三", 20, "男", "20230818001" };
	printf("name: %s\n", s.name);
	printf("age : %d\n", s.age);
	printf("sex : %s\n", s.sex);
	printf("id : %s\n", s.id);

	//按照指定的顺序初始化
	struct Stu s2 = { .age = 18, .name = "lisi", .id = "20230818002", .sex = "女"};
	printf("name: %s\n", s2.name);
	printf("age : %d\n", s2.age);
	printf("sex : %s\n", s2.sex);
	printf("id : %s\n", s2.id);
	
	return 0;
}

运行结果如图:
在这里插入图片描述

1.2 结构的特殊声明

在声明结构的时候，可以不完全的声明。

比如：

//匿名结构体类型
struct
{
	int a;
	char b;
	float c;
}x;

struct
{
	int a;
	char b;
	float c;
}*p;

上⾯的两个结构在声明的时候省略掉了结构体标签（tag）。那么问题来了？

//在上⾯代码的基础上，下⾯的代码合法吗？
p = &x;

警告：

  • 编译器会把上⾯的两个声明当成完全不同的两个类型，所以是非法的。
  • 匿名的结构体类型，如果没有对结构体类型重命名的话，基本上只能使用⼀次。

1.3 结构的自引用

在结构中包含⼀个类型为该结构本⾝的成员是否可以呢？

比如，定义⼀个链表的节点：

struct Node
{
 int data;
 struct Node next;
};

上述代码正确吗？如果正确，那 sizeof(struct Node) 是多少？

仔细分析，其实是不⾏的，因为⼀个结构体中再包含⼀个同类型的结构体变量，这样结构体变量的⼤⼩就会⽆穷的⼤，是不合理的。

正确的自引用方式：

struct Node
{
	int data;//存放数据
	struct Node* next;//存放下一个节点的地址
};

在结构体⾃引⽤使⽤的过程中，夹杂了 typedef 对匿名结构体类型重命名，也容易引⼊问题，看看下⾯的代码，可行吗？

typedef struct
{
	int data;
	Node* next;
}Node;

答案是不⾏的，因为Node是对前⾯的匿名结构体类型的重命名产⽣的，但是在匿名结构体内部提前使⽤Node类型来创建成员变量，这是不⾏的。

解决方案如下：定义结构体不要使用匿名结构体了

typedef struct Node
{
	int data;
	struct Node* next;
}Node;

2. 结构体内存对齐

现在我们深⼊讨论⼀个问题：计算结构体的大小。这也是⼀个特别热⻔的考点: 结构体内存对齐

2.1 对齐规则

首先得掌握结构体的对齐规则：

  1. 结构体的第⼀个成员对⻬到和结构体变量起始位置偏移量为0的地址处

  2. 其他成员变量要对⻬到某个数字（对⻬数）的整数倍的地址处。
    对齐数 = 编译器默认的一个对齐数与该成员变量大小的较小值。

    - 结构体内存对齐VS 中默认的值为 8

    - Linux中 gcc 没有默认对齐数，对⻬数就是成员自身的大小

  3. 结构体总⼤⼩为最⼤对⻬数（结构体中每个成员变量都有⼀个对⻬数，所有对⻬数中最⼤的）的整数倍。

  4. 如果嵌套了结构体的情况，嵌套的结构体成员对齐到自己的成员中最大对齐数的整数倍处，结构体的整体大小就是所有最⼤对⻬数（含嵌套结构体中成员的对⻬数）的整数倍。

2.1.1 练习1:
//练习1
#include <stdio.h>
struct S1
{
	char c1;//0(偏移量为0的地址上)
	char c2;//1
	//因为是int,根据规则二,要对齐到4的的整数倍的地址处
	int i;//4~7
	//0~7一共7个字节
};

int main()
{
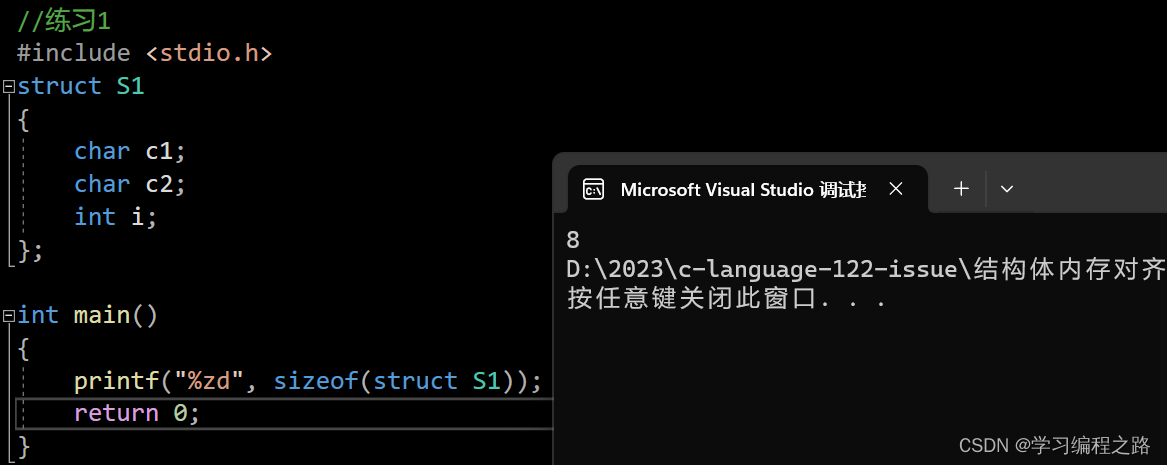
	printf("%zd", sizeof(struct S1));
	return 0;
}

运行结果如图:
在这里插入图片描述

2.1.2 练习2:
//练习2:
#include <stdio.h>
struct S2
{
	char c1;//0(偏移量为0的地址上)
	int i;//4~7
	char c2;//8
	//对齐到4的整数倍,9~11,总共12个字节
};

int main()
{
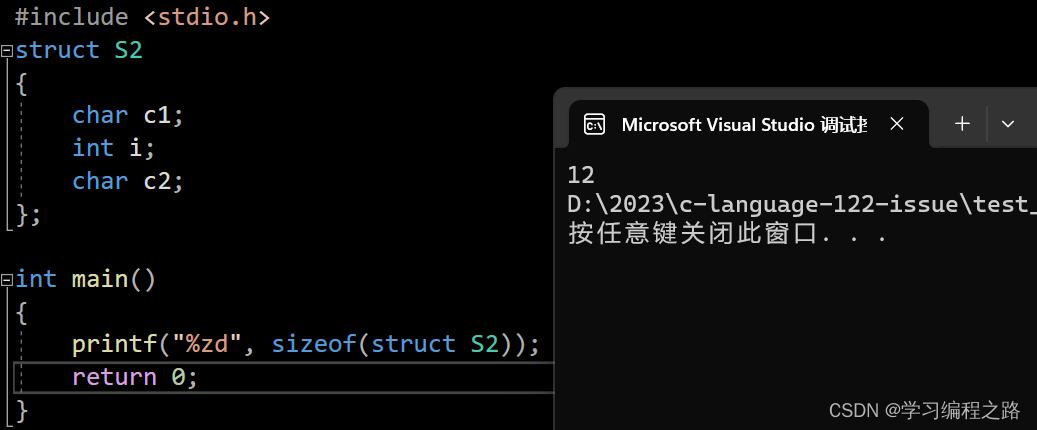
	printf("%zd", sizeof(struct S2));
	return 0;
}

运行结果如图:
在这里插入图片描述

2.1.3 练习3:
//练习3
#include <stdio.h>
struct S3
{
	double d;//0~7
	char c;//8
	int i;//12~15
	//一共16个字节
};

int main()
{
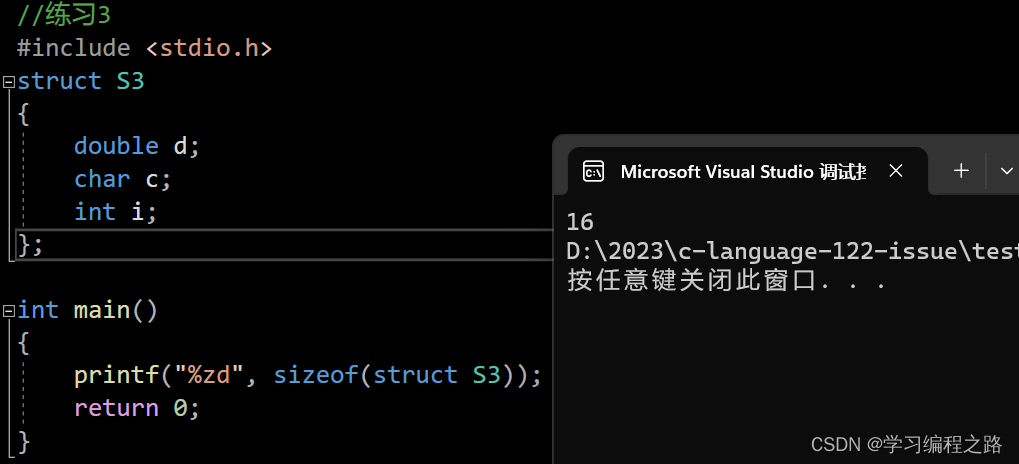
	printf("%zd", sizeof(struct S3));
	return 0;
}

运行结果如图:
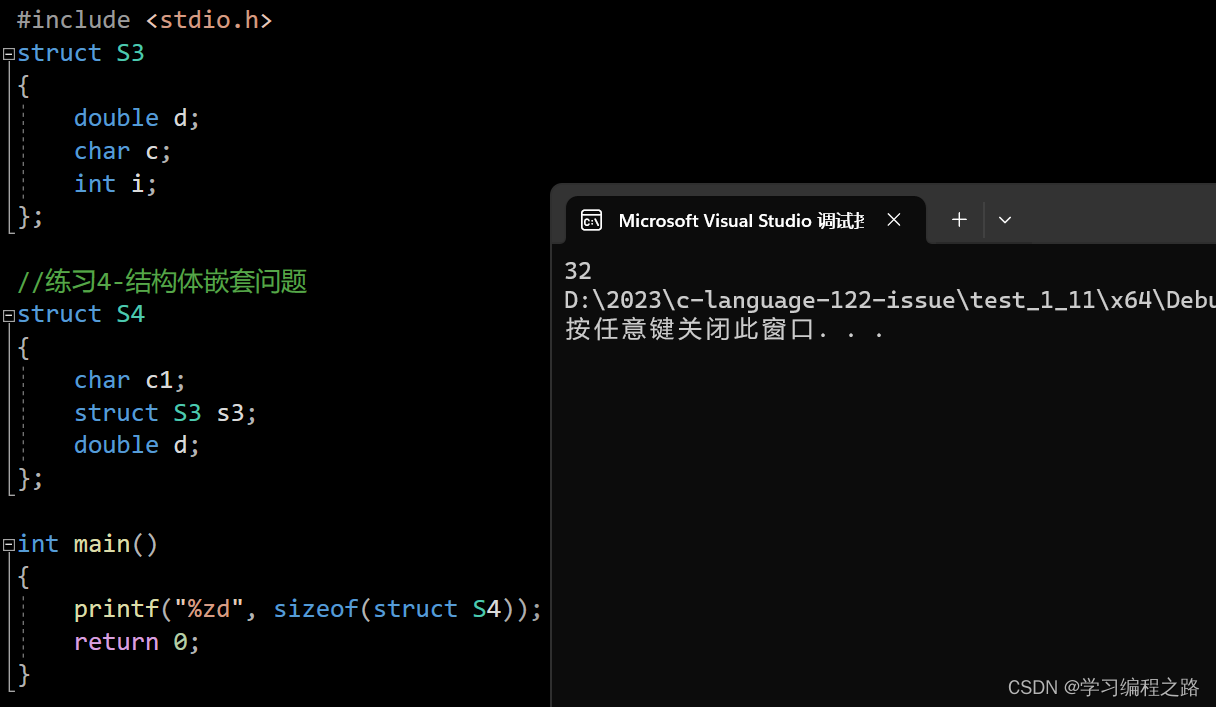
在这里插入图片描述

2.1.4 练习4:
//练习4-结构体嵌套问题
#include <stdio.h>
struct S3
{
	double d;
	char c;
	int i;
};

struct S4
{
	char c1;//0
	struct S3 s3;//8~23(嵌套的结构体成员对齐到自己的成员中最大对齐数的整数倍处)
	double d;//24~31
	//一共32个字节
};

int main()
{
	printf("%zd", sizeof(struct S4));
	return 0;
}

运行结果如图:
在这里插入图片描述

2.2 offsetof宏的使用

在这里插入图片描述

offsetof (type,member)
  • offsetof - 计算结构体成员相较于起始位置的偏移量
  • 第一个参数是结构体类型，第二个参数是结构体成员名
  • 使用offsetof宏需要包含头文件 #include <stddef.h>

代码举例:

#include <stdio.h>
#include <stddef.h>
struct S3
{
	double d;
	char c;
	int i;
};

//练习4-结构体嵌套问题
struct S4
{
	char c1;
	struct S3 s3;
	double d;
};

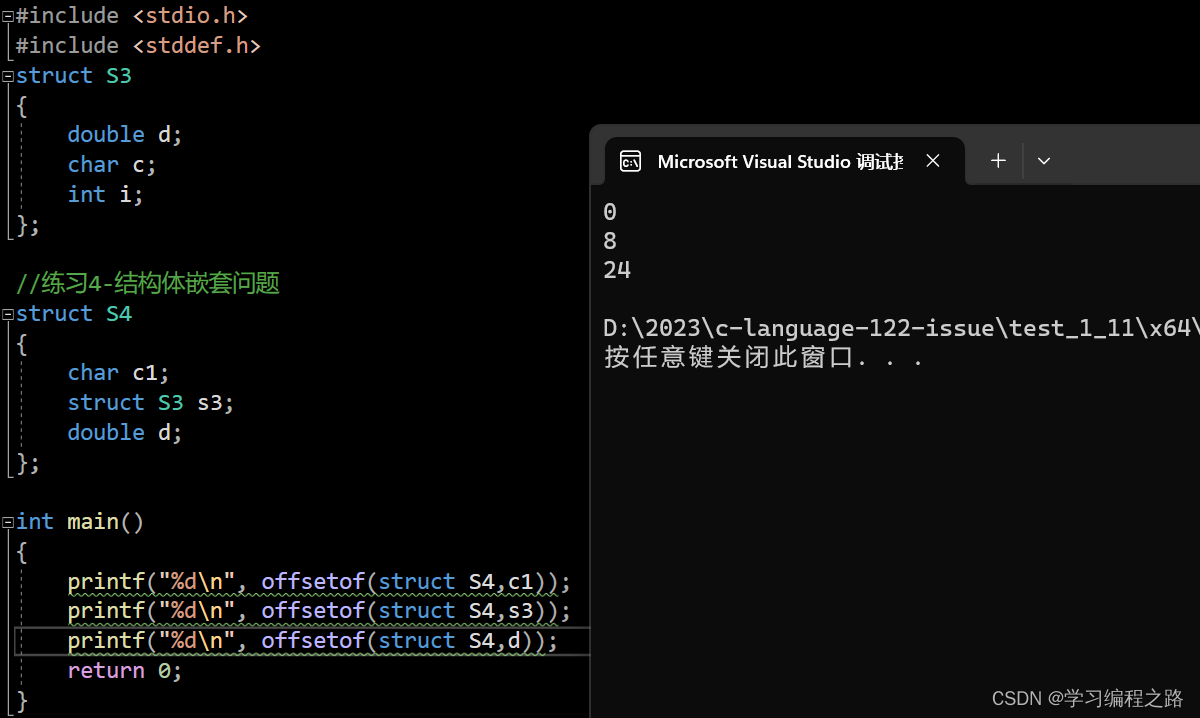
int main()
{
	printf("%d\n", offsetof(struct S4,c1));
	printf("%d\n", offsetof(struct S4,s3));
	printf("%d\n", offsetof(struct S4,d));
	return 0;
}

运行结果如图:
在这里插入图片描述

2.3 为什么存在内存对齐?

大部分的参考资料都是这样说的：

  1. 平台原因 (移植原因)：
    不是所有的硬件平台都能访问任意地址上的任意数据的；某些硬件平台只能在某些地址处取某些特定类型的数据，否则抛出硬件异常。
  2. 性能原因：
    数据结构(尤其是栈)应该尽可能地在⾃然边界上对齐。原因在于，为了访问未对⻬的内存，处理器需要作两次内存访问；⽽对⻬的内存访问仅需要⼀次访问。假设⼀个处理器总是从内存中取8个字节，则地址必须是8的倍数。如果我们能保证将所有的double类型的数据的地址都对⻬成8的倍数，那么就可以⽤⼀个内存操作来读或者写值了。否则，我们可能需要执⾏两次内存访问，因为对象可能被分放在两个8字节内存块中。

那在设计结构体的时候，我们既要满⾜对⻬，⼜要节省空间，如何做到：

让占用空间小的成员尽量集中在一起

总体来说：结构体的内存对齐是拿空间来换取时间的做法。

 //例如：
struct S1
{
	char c1;
	int i;
	char c2;
	};

struct S2
{
	char c1;
	char c2;
	int i;
};

S1 和 S2 类型的成员⼀模⼀样，但是 S1 和 S2 所占空间的大小有了⼀些区别。

2.4 修改默认对齐数

#pragma 这个预处理指令，可以改变编译器的默认对齐数。

#include <stdio.h>
#pragma pack(1)//设置默认对齐数为1
struct S
{
	char c1;
	int i;
	char c2;
};
#pragma pack()//取消设置的对齐数，还原为默认
int main()
{
	//输出的结果是什么？
	printf("%d\n", sizeof(struct S));
	return 0;
}

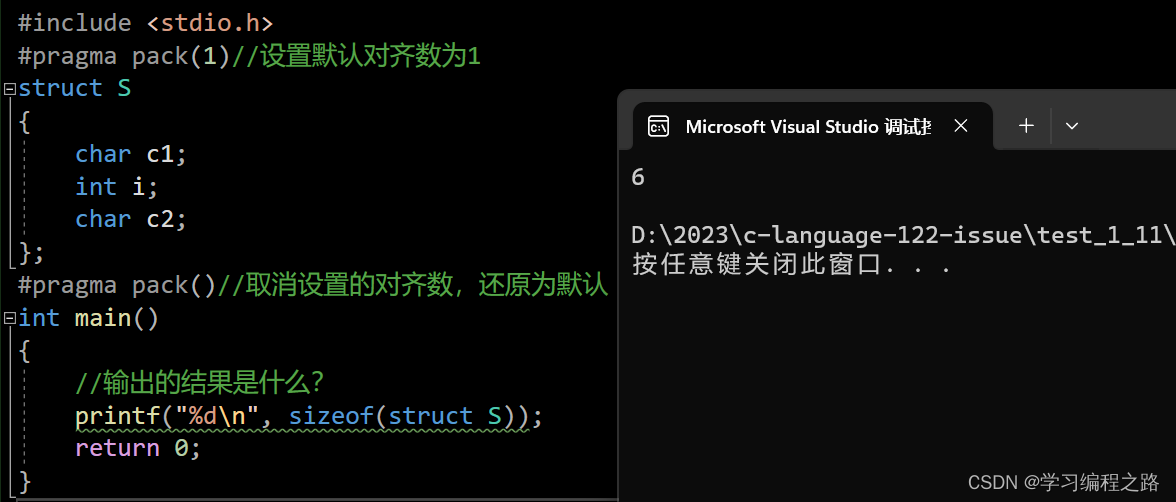
在这里插入图片描述

结构体在对齐方式不合适的时候，我们可以自己更改默认对齐数。

3. 结构体传参

3.1 代码一

#include <stdio.h>

struct S
{
	int data[1000];
	int num;
};

void print1(struct S t)
{
	printf("%d %d\n", t.data[0], t.num);

}

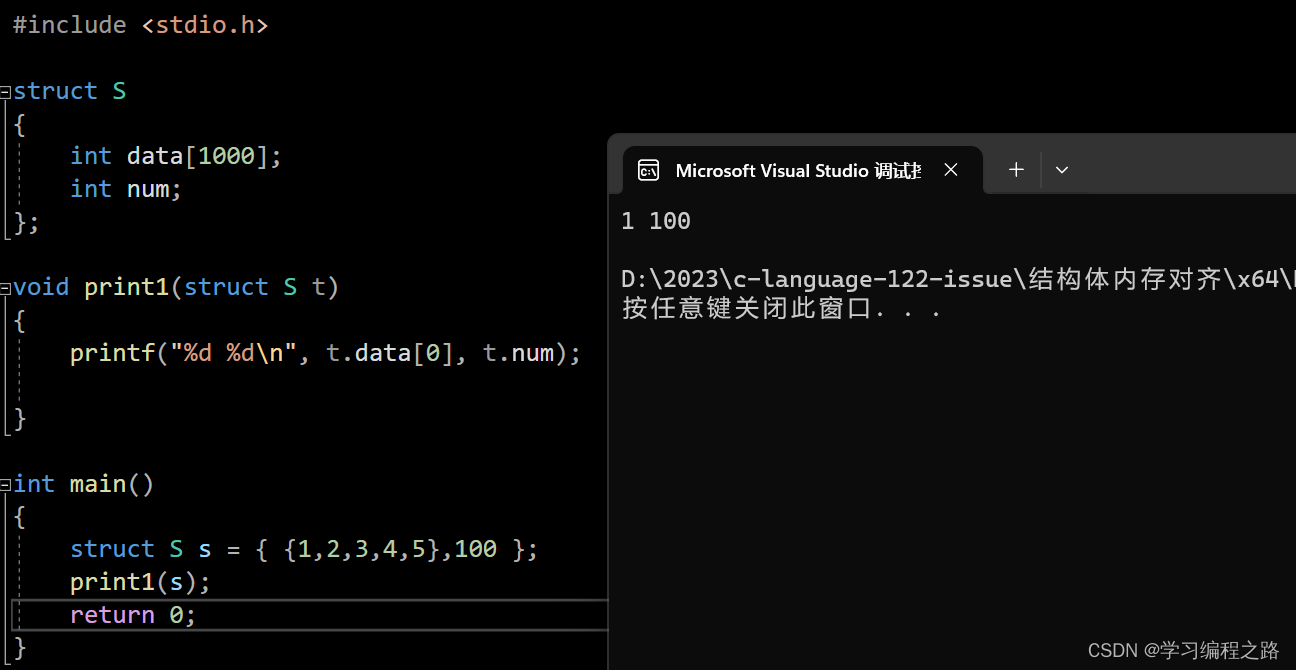
int main()
{
	struct S s = { {1,2,3,4,5},100 };
	print1(s);
	return 0;
}

运行结果如图:
在这里插入图片描述

3.2 代码二

#include <stdio.h>

struct S
{
	int data[1000];
	int num;
};

void print1(struct S t)
{
	printf("%d %d\n", t.data[0], t.num);

}

void print2(struct S* ps)
{
	printf("%d %d\n", ps->data[0], ps->num);
}

int main()
{
	struct S s = { {1,2,3,4,5},100 };
	print1(s);
	print2(&s);
	return 0;
}

运行结果如图:
在这里插入图片描述

上面的 print1 和 print2 函数哪个好些？

答案是：首选print2函数。

原因：

函数传参的时候，参数是需要压栈，会有时间和空间上的系统开销。

如果传递⼀个结构体对象的时候，结构体过大，参数压栈的的系统开销⽐较⼤，所以会导致性能的下降。

结论：
结构体传参的时候，要传结构体的地址。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1401272.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

蓝桥杯省赛无忧 编程7

蓝桥杯省赛无忧 编程7

为了解决这个问题&#xff0c;我们可以编写一个函数来计算从编号为1的石头到达编号为n的石头所需的最少步数。问题的关键是理解每一步的移动规则&#xff1a;从当前石头编号n移动到编号为nx的石头上&#xff0c;其中x是n的各位数字之和。因此&#xff0c;我们需要一个辅助函数来…
阅读更多...
docker 部署 sentinel

docker 部署 sentinel

docker 部署 sentinel 环境安装 拉取镜像 目前稳定的版本是1.8.0 docker pull bladex/sentinel-dashboard:1.8.0启动服务 docker run --name sentinel -p 8858:8858 -td bladex/sentinel-dashboard:1.8.0登录 登录的时候账号和密码都是sentinel
阅读更多...
[安全警报] Npm木马利用“Oscompatible“包悄然安装AnyDesk

[安全警报] Npm木马利用“Oscompatible“包悄然安装AnyDesk

最近&#xff0c;一个名为OsCompatible的恶意包被上传到npm 。该包被发现包含一个针对 Windows 的远程访问木马。 这个名为OsCompatible的软件包于2024年1月9日发布&#xff0c;在被撤下之前共吸引了380次下载。 据了解&#xff0c;OsCompatible包含“几个奇怪的二进制文件”…
阅读更多...
解决 pnpm : 无法加载文件 C:\Program Files\nodejs\pnpm.ps1，因为在此系统上禁止运行脚本。

解决 pnpm : 无法加载文件 C:\Program Files\nodejs\pnpm.ps1，因为在此系统上禁止运行脚本。

执行下面命令进行安装pnpm安装后 npm install -g pnpm 然后执行pnpm 报错 解决办法&#xff1a; 以管理员身份运行 Windows PowerShell &#xff0c; 在命令行输入以下命令后按回车&#xff0c; set-ExecutionPolicy RemoteSigned 再输入Y 回车即可。 再回到控制台输入p…
阅读更多...
Elasticsearch Index Shard Allocation 索引分片分配策略

Elasticsearch Index Shard Allocation 索引分片分配策略

Elasticsearch 索引分片的分配策略说明 在上一篇《索引生命周期管理ILM看完不懂你锤我 》&#xff08;https://mp.weixin.qq.com/s/ajhFp-xBU1dJm8a1dDdRQQ&#xff09;中&#xff0c;我们已经学会了索引级别的分片分配过滤属性&#xff0c;也就是在配置文件中指定当前节点的属…
阅读更多...
srm-50——攻防世界

srm-50——攻防世界

可以知道这道题是二类题型&#xff0c;你完成某个事情给你flag 我们输入正确的东西&#xff0c;给“flag” 运行一下可以知道这些关键词 直接关键词在字符串里面 找到运行得到的东西 INT_PTR __stdcall DialogFunc(HWND hDlg, UINT a2, WPARAM a3, LPARAM a4) {HMODULE Mo…
阅读更多...
Vue 组件通信方式

Vue 组件通信方式

✨ 专栏介绍 在当今Web开发领域中&#xff0c;构建交互性强、可复用且易于维护的用户界面是至关重要的。而Vue.js作为一款现代化且流行的JavaScript框架&#xff0c;正是为了满足这些需求而诞生。它采用了MVVM架构模式&#xff0c;并通过数据驱动和组件化的方式&#xff0c;使…
阅读更多...
天津想转行学python培训班靠谱吗？

天津想转行学python培训班靠谱吗？

现在的职业如此繁多&#xff0c;很多人把高薪当成衡量工作好坏的重要标准&#xff0c;因此IT行业以超出其他行业几倍薪资水平成为不错的选择&#xff0c;而Python又以其简单易学好上手成为大家所青睐的学习目标。 Python发展前景如何 Python语言就业发展方向广泛&#xff1a;…
阅读更多...
SpringSecurity+OAuth2.0 搭建认证中心和资源服务中心

SpringSecurity+OAuth2.0 搭建认证中心和资源服务中心

目录 1. OAuth2.0 简介 2. 代码搭建 2.1 认证中心&#xff08;8080端口&#xff09; 2.2 资源服务中心&#xff08;8081端口&#xff09; 3. 测试结果 1. OAuth2.0 简介 OAuth 2.0&#xff08;开放授权 2.0&#xff09;是一个开放标准&#xff0c;用于授权第三方应用程序…
阅读更多...
java垃圾回收GC过程

java垃圾回收GC过程

GC&#xff08;Gabage Collection&#xff09; 用于回收堆中的垃圾数据 清理方法 1.标记-清理 对数据标记&#xff0c;然后清理 缺点&#xff1a;容易产生内存碎片 2.标记-整理 对标记后的数据清理&#xff0c;剩下数据前移 缺点&#xff1a;每次清理后数据都要迁移&#xff0…
阅读更多...
代码随想录二刷 ｜ 回溯 ｜ 组合优化

代码随想录二刷 ｜ 回溯 ｜ 组合优化

代码随想录二刷 &#xff5c; 回溯 &#xff5c; 组合优化 剪枝优化 剪枝优化 在遍历的过程中有如下代码&#xff1a; for (int i startIndex; i < n; i) {path.pop_back();backtracking(n, k, i 1);path.pop_back(); }n 4&#xff0c;k 4的话&#xff0c;那么第一层f…
阅读更多...
qemu使用

qemu使用

百度qemu bios 问题 坑爹的玩意&#xff0c;编译qemu 还需要python3.5以上 解决方法&#xff1a; CentOS7安装Python3.8-CSDN博客 https://www.cnblogs.com/Oliver.net/p/7211967.html 编译python3.8还由于openssl过低 参考 QEMU启动x86-Linux内核_qemu-system-x86-…
阅读更多...
SaaS多租户篇

SaaS多租户篇

文章目录 1. 多租户是什么2. 技术组件2.1 如何实现多租户的DB封装2.2 如何实现多租户的redis封装2.3 如何实现多租户的Web和Security封装2.4 如何实现多租户的Job封装2.5 如何实现多租户的 MQ 与 Async 封装&#xff1f;2.6 如何实现多租户的 AOP 与 Util 封装&#xff1f; 3.业…
阅读更多...
【Qt之模型视图】5. Qt库提供的视图便捷类

【Qt之模型视图】5. Qt库提供的视图便捷类

1. 前言 Qt提供了一些便捷的视图类&#xff0c;如QListWidget提供项目列表&#xff0c;QTreeWidget显示多级树结构&#xff0c;QTableWidget提供单元格项的表格。每个类都继承了QAbstractItemView类的行为&#xff0c;QAbstractItemView类实现了项目选择和标题管理的通用行为。…
阅读更多...
《WebKit 技术内幕》之五（1）： HTML解释器和DOM 模型

《WebKit 技术内幕》之五（1）： HTML解释器和DOM 模型

第五章 HTML 解释器和 DOM 模型 1.DOM 模型 1.1 DOM标准 DOM &#xff08;Document Object Model&#xff09;的全称是文档对象模型&#xff0c;它可以以一种独立于平台和语言的方式访问和修改一个文档的内容和结构。这里的文档可以是 HTML 文档、XML 文档或者 XHTML 文档。D…
阅读更多...
ubuntu 相关内容

ubuntu 相关内容

ubuntu 优盘安装&#xff1a; 台式机安装纯ubuntu系统的操作步骤-CSDN博客https://blog.csdn.net/youngwah292/article/details/127032009?ops_request_misc%257B%2522request%255Fid%2522%253A%2522170583039216800213099577%2522%252C%2522scm%2522%253A%252220140713.1301…
阅读更多...
音视频开发ffmpeg

音视频开发ffmpeg

ffmpeg数据结构 重要的结构体 压缩数据 avpacket 帧数据 avframe 管家&#xff1a; avformatcontext 格式上下文 文件是一种协议 解协议&#xff08;http、rtsp rtmp mms tcp udp…&#xff09; AVIOContext URLProtocol URLContext存储音视频中的协议类型和状态 有缓冲区…
阅读更多...
74.搜索二维矩阵 - 力扣（LeetCode）

74.搜索二维矩阵 - 力扣（LeetCode）

题目描述 给你一个满足下述两条属性的 m x n 整数矩阵&#xff1a; 每行中的整数从左到右按非严格递增顺序排列。 每行的第一个整数大于前一行的最后一个整数。 给你一个整数 target &#xff0c;如果 target 在矩阵中&#xff0c;返回 true &#xff1b;否则&#xff0c;返回…
阅读更多...
爬虫案例—雪球网行情中心板块数据抓取

爬虫案例—雪球网行情中心板块数据抓取

爬虫案例—雪球网行情中心板块数据抓取 雪球网行情中心网址&#xff1a;https://xueqiu.com/hq 目标&#xff1a;市场一览板块、热股榜板块、新股预告板块、关注排行榜板块 import datetimeimport requestsheaders {user-agent: Mozilla/5.0 (Macintosh; Intel Mac OS X 10…
阅读更多...
算法优化：LeetCode第122场双周赛解题策略与技巧

算法优化：LeetCode第122场双周赛解题策略与技巧

接下来会以刷常规题为主 &#xff0c;周赛的难题想要独立做出来还是有一定难度的&#xff0c;需要消耗大量时间 比赛地址 3011. 判断一个数组是否可以变为有序 public class Solution {public int minimumCost(int[] nums) {if (nums.length < 3) {// 数组长度小于3时&a…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023