一，题目

SPOJ PT07Z, Longest path in a tree

---

一.定义

树上任意两节点之间最长的简单路径即为树的「直径」。

---

二，解法

做法 1. 两次 DFS

过程:

首先从任意节点y, 开始进行第一次 DFS，到达距离其最远的节点，记为 z，然后再从 z开始做第二次 DFS，到达距离z 最远的节点，记为z' ，则 f(z,z')即为树的直径。

显然，如果第一次 DFS 到达的节点 z是直径的一端，那么第二次 DFS 到达的节点z' 一定是直径的另外一端。我们只需证明在任意情况下，z必为直径的一端。

定理：

在一棵树上，从任意节点 y开始进行一次 DFS，到达的距离其最远的节点z 必为直径的一端。

证明:

注意事项:

1.

上述证明过程建立在所有路径均不为负的前提下。如果树上存在负权边，则上述证明不成立。

所以:

故若存在 负权边，则无法使用 两次 DFS 的方式求解 直径。

2.

如果需要求出一条直径上所有的节点，则可以在第二次 DFS 的过程中，记录每个点的前序节点，即可从直径的一端一路向前，遍历直径上所有的节点。

代码实现:

#include <bits/stdc++.h>
const int N = 10000 + 10;
using namespace std;

int n, c, d[N];
vector<int> E[N];

void dfs(int u, int fa) {
  for (int v : E[u]) {
    if (v == fa) continue;
    d[v] = d[u] + 1;
    if (d[v] > d[c]) c = v;
    dfs(v, u);
  }
}

int main() {
  scanf("%d", &n);
  for (int i = 1; i < n; i++) {
    int u, v;
    scanf("%d %d", &u, &v);
    E[u].push_back(v), E[v].push_back(u);
  }
  dfs(1, 0);
  d[c] = 0, dfs(c, 0);
  printf("%d\n", d[c]);
  return 0;
}

做法 2.树形 DP

过程:

我们记录当 1的根时，每个节点作为子树的根向下，所能延伸的最远距离d1 ，和次远距离d2 ，那么直径就是所有 d1+d2的最大值。

树形 DP 可以在存在负权边的情况下求解出树的直径。

性质:

若树上所有边边权均为正，则树的所有直径中点重合

注意事项:

如果需要求出一条直径上所有的节点，则可以在 DP 的过程中，记录下每个节点能向下延伸的最远距离与次远距离所对应的子节点，之后再找到对应的u ，使得

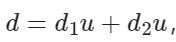
，即可分别沿着从u 开始的最远距离和次远距离对应的子节点一路向下，遍历直径上所有的节点。

证明:

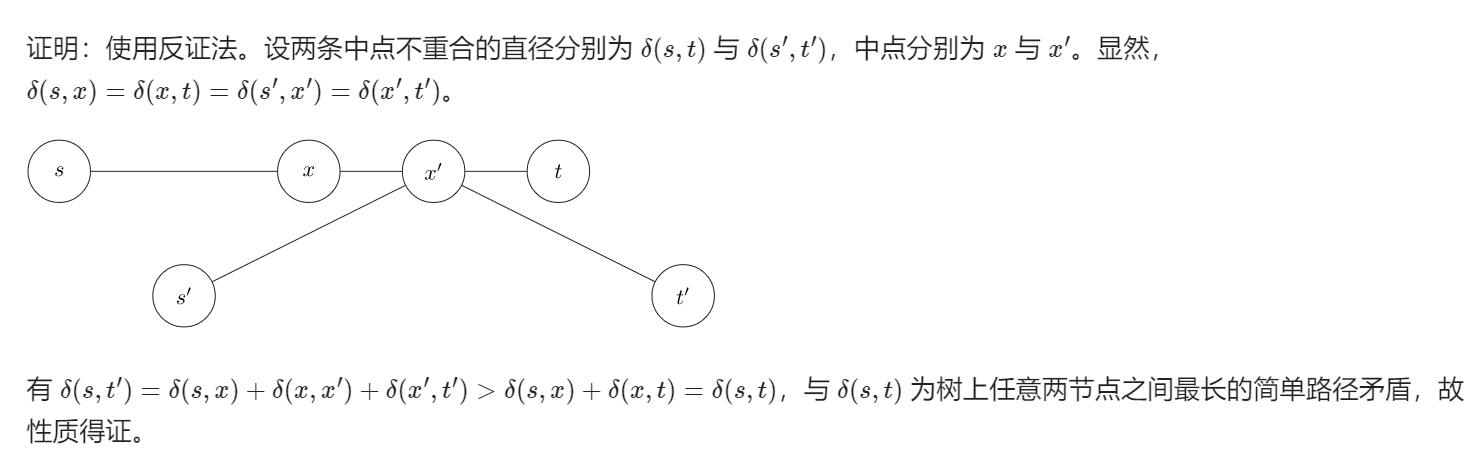
代码实现:

#include <bits/stdc++.h>
const int N = 10000 + 10;
using namespace std;
int n,d = 0;
int d1[N], d2[N];
vector<int> E[N];
void dfs(int u, int fa)
{
  d1[u] = d2[u] = 0;
  for(int v : E[u])
  {
    if(v == fa) continue;
    dfs(v,u);
    int t = d1[v] + 1;
    if(t > d1[u])
    {
      d2[u] = d1[u];
      d1[u] = t;
    }
    else if(t > d2[u]) d2[u] = t;
  }
  d = max(d,d1[u] + d2[u]);
}
int main()
{
  scanf("%d",&n);
  for(int i = 1; i < n; i++)
  {
    int u,v;
    scanf("%d%d",&u,&v);
    E[u].push_back(v);
    E[v].push_back(u);
  }
  dfs(1,0);
  printf("%d\n", d);
  return 0;
}