文章目录
- 1 感知机的直观理解
- 2 感知机的数学角度
- 3 代码实现
- 4 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 感知机的直观理解
感知机应该属于机器学习算法中最简单的一种算法,其原理可以看下图:
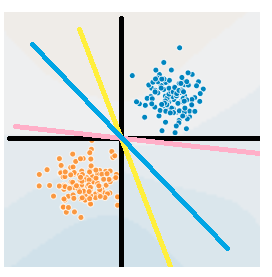
比如说我们有一个坐标轴(图中的黑色线),横的为x1轴,竖的x2轴。图中的每一个点都是由(x1,x2)决定的。如果我们将这张图应用在判断零件是否合格上,x1表示零件长度,x2表示零件质量,坐标轴表示零件的均值长度和均值重量,并且蓝色的为合格产品,黄色为劣质产品,需要剔除。那么很显然如果零件的长度和重量都大于均值,说明这个零件是合格的。也就是在第一象限的所有蓝色点。反之如果两项都小于均值,就是劣质的,比如在第三象限的黄色点。
在预测上很简单,拿到一个新的零件,我们测出它的长度x1,质量x2,如果两项都大于均值,说明零件合格。这就是我们人的人工智能。
那么程序怎么知道长度重量都大于均值的零件就是合格的呢?
或者说
它是怎么学会这个规则的呢?
程序拿到手的是当前图里所有点的信息以及标签,也就是说它知道所有样本x的坐标为(x1, x2),同时它属于蓝色或黄色。对于目前手里的这些点,要是能找到一条直线把它们分开就好了,这样我拿到一个新的零件,知道了它的质量和重量,我就可以判断它在线的哪一侧,就可以知道它可能属于好的或坏的零件了。例如图里的黄、蓝、粉三条线,都可以完美地把当前的两种情况划分开。甚至x1坐标轴或x2坐标轴都能成为一个划分直线(这两个直线均能把所有点正确地分开)。
读者也看到了,对于图中的两堆点,我们有无数条直线可以将其划分开,事实上我们不光要能划分当前的点,当新来的点进来是,也要能很好地将其划分,所以哪条线最好呢?
怎样一条直线属于最佳的划分直线?实际上感知机无法找到一条最佳的直线,它找到的可能是图中所有画出来的线,只要能把所有的点都分开就好了。
得出结论:
如果一条直线能够不分错一个点,那就是一条好的直线
进一步来说:
如果我们把所有分错的点和直线的距离求和,让这段求和的举例最小(最好是0,这样就表示没有分错的点了),这条直线就是我们要找的。
2 感知机的数学角度
首先我们确定一下终极目标:甭管找最佳划分直线啥中间乱七八糟的步骤,反正最后生成一个函数f(x),当我们把新的一个数据x扔进函数以后,它会预测告诉我这是蓝的还是黄的,多简单啊。所以我们不要去考虑中间过程,先把结果定了。
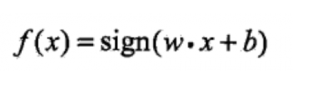
瞧,f(x)不是出来了嘛,sign是啥?wx+b是啥?别着急,我们再看一下sigin函数是什么。
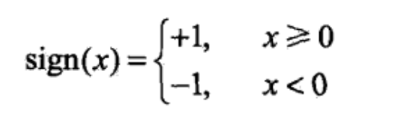
sign好像很简单,当x大于等于0,sign输出1,否则输出-1。那么往前递归一下,wx+b如果大于等于0,f(x)就等于1,反之f(x)等于-1。
那么wx+b是啥?
它就是那条最优的直线。我们把这个公式放在二维情况下看,二维中的直线是这样定义的:y=ax+b。在二维中,w就是a,b还是b。所以wx+b是一条直线(比如说本文最开始那张图中的蓝线)。如果新的点x在蓝线左侧,那么wx+b<0,再经过sign,最后f输出-1,如果在右侧,输出1。等等,好像有点说不通,把情况等价到二维平面中,y=ax+b,只要点在x轴上方,甭管点在线的左侧右侧,最后结果都是大于0啊,这个值得正负跟线有啥关系?emmm….其实wx+b和ax+b表现直线的形式一样,但是又稍有差别。我们把最前头的图逆时针旋转45度,蓝线是不是变成x轴了?哈哈这样是不是原先蓝线的右侧变成了x轴的上方了?其实感知机在计算wx+b这条线的时候,已经在暗地里进行了转换,使得用于划分的直线变成x轴,左右侧分别为x轴的上方和下方,也就成了正和负。
那么,为啥是wx+b,而不叫ax+b?
在本文中使用零件作为例子,上文使用了长度和重量(x1,x2)来表示一个零件的属性,所以一个二维平面就足够,那么如果零件的品质和色泽也有关系呢?那就得加一个x3表示色泽,样本的属性就变成了(x1,x2,x3),变成三维了。wx+b并不是只用于二维情况,在三维这种情况下,仍然可以使用这个公式。所以wx+b与ax+b只是在二维上近似一致,实际上是不同的东西。在三维中wx+b是啥?我们想象屋子里一个角落有蓝点,一个角落有黄点,还用一条直线的话,显然是不够的,需要一个平面!所以在三维中,wx+b是一个平面!至于为什么,后文会详细说明。四维呢?emmm…好像没法描述是个什么东西可以把四维空间分开,但是对于四维来说,应该会存在一个东西像一把刀一样把四维空间切成两半。能切成两半,应该是一个对于四维来说是个平面的东西,就像对于三维来说切割它的是一个二维的平面,二维来说是一个一维的平面。总之四维中wx+b可以表示为一个相对于四维来说是个平面的东西,然后把四维空间一切为二,我们给它取名叫超平面。由此引申,在高维空间中,wx+b是一个划分超平面,这也就是它正式的名字。
正式来说:
wx+b是一个n维空间中的超平面S,其中w是超平面的法向量,b是超平面的截距,这个超平面将特征空间划分成两部分,位于两部分的点分别被分为正负两类,所以,超平面S称为分离超平面。
细节:
w是超平面的法向量:对于一个平面来说w就是这么定义的,是数学知识,可以谷歌补习一下
b是超平面的截距:可以按照二维中的ax+b理解
特征空间:也就是整个n维空间,样本的每个属性都叫一个特征,特征空间的意思是在这个空间中可以找到样本所有的属性组合

我们从最初的要求有个f(x),引申到能只输出1和-1的sign(x),再到现在的wx+b,看起来越来越简单了,只要能找到最合适的wx+b,就能完成感知机的搭建了。前文说过,让误分类的点距离和最大化来找这个超平面,首先我们要放出单独计算一个点与超平面之间距离的公式,这样才能将所有的点的距离公式求出来对不?

先看wx+b,在二维空间中,我们可以认为它是一条直线,同时因为做过转换,整张图旋转后wx+b是x轴,那么所有点到x轴的距离其实就是wx+b的值对不?当然了,考虑到x轴下方的点,得加上绝对值->|wx+b|,求所有误分类点的距离和,也就是求|wx+b|的总和,让它最小化。很简单啊,把w和b等比例缩小就好啦,比如说w改为0.5w,b改为0.5b,线还是那条线,但是值缩小两倍啦!你还不满意?我可以接着缩!缩到0去!所以啊,我们要加点约束,让整个式子除以w的模长。啥意思?就是w不管怎么样,要除以它的单位长度。如果我w和b等比例缩小,那||w||也会等比例缩小,值一动不动,很稳。没有除以模长之前,|wx+b|叫函数间隔,除模长之后叫几何间隔,几何间隔可以认为是物理意义上的实际长度,管你怎么放大缩小,你物理距离就那样,不可能改个数就变。在机器学习中求距离时,通常是使用几何间隔的,否则无法求出解。

对于误分类的数据,例如实际应该属于蓝色的点(线的右侧,y>0),但实际上预测出来是在左侧(wx+b<0),那就是分错了,结果是负,这时候再加个符号,结果就是正了,再除以w的模长,就是单个误分类的点到超平面的举例。举例总和就是所有误分类的点相加。
上图最后说不考虑除以模长,就变成了函数间隔,为什么可以这么做呢?不考虑wb等比例缩小这件事了吗?上文说的是错的吗?
有一种解释是这样说的:感知机是误分类驱动的算法,它的终极目标是没有误分类的点,如果没有误分类的点,总和距离就变成了0,w和b值怎样都没用。所以几何间隔和函数间隔在感知机的应用上没有差别,为了计算简单,使用函数间隔。

以上是损失函数的正式定义,在求得划分超平面的终极目标就是让损失函数最小化,如果是0的话就相当完美了。

感知机使用梯度下降方法求得w和b的最优解,从而得到划分超平面wx+b,关于梯度下降及其中的步长受篇幅所限可以自行谷歌。
3 代码实现
#coding=utf-8
#Author:Dodo
#Date:2018-11-15
#Email:lvtengchao@pku.edu.cn
'''
数据集:Mnist
训练集数量:60000
测试集数量:10000
------------------------------
运行结果:
正确率:81.72%(二分类)
运行时长:78.6s
'''
import numpy as np
import time
def loadData(fileName):
'''
加载Mnist数据集
:param fileName:要加载的数据集路径
:return: list形式的数据集及标记
'''
print('start to read data')
# 存放数据及标记的list
dataArr = []; labelArr = []
# 打开文件
fr = open(fileName, 'r')
# 将文件按行读取
for line in fr.readlines():
# 对每一行数据按切割福','进行切割,返回字段列表
curLine = line.strip().split(',')
# Mnsit有0-9是个标记,由于是二分类任务,所以将>=5的作为1,<5为-1
if int(curLine[0]) >= 5:
labelArr.append(1)
else:
labelArr.append(-1)
#存放标记
#[int(num) for num in curLine[1:]] -> 遍历每一行中除了以第一哥元素(标记)外将所有元素转换成int类型
#[int(num)/255 for num in curLine[1:]] -> 将所有数据除255归一化(非必须步骤,可以不归一化)
dataArr.append([int(num)/255 for num in curLine[1:]])
#返回data和label
return dataArr, labelArr
def perceptron(dataArr, labelArr, iter=50):
'''
感知器训练过程
:param dataArr:训练集的数据 (list)
:param labelArr: 训练集的标签(list)
:param iter: 迭代次数,默认50
:return: 训练好的w和b
'''
print('start to trans')
#将数据转换成矩阵形式(在机器学习中因为通常都是向量的运算,转换称矩阵形式方便运算)
#转换后的数据中每一个样本的向量都是横向的
dataMat = np.mat(dataArr)
#将标签转换成矩阵,之后转置(.T为转置)。
#转置是因为在运算中需要单独取label中的某一个元素,如果是1xN的矩阵的话,无法用label[i]的方式读取
#对于只有1xN的label可以不转换成矩阵,直接label[i]即可,这里转换是为了格式上的统一
labelMat = np.mat(labelArr).T
#获取数据矩阵的大小,为m*n
m, n = np.shape(dataMat)
#创建初始权重w,初始值全为0。
#np.shape(dataMat)的返回值为m,n -> np.shape(dataMat)[1])的值即为n,与
#样本长度保持一致
w = np.zeros((1, np.shape(dataMat)[1]))
#初始化偏置b为0
b = 0
#初始化步长,也就是梯度下降过程中的n,控制梯度下降速率
h = 0.0001
#进行iter次迭代计算
for k in range(iter):
#对于每一个样本进行梯度下降
#李航书中在2.3.1开头部分使用的梯度下降,是全部样本都算一遍以后,统一
#进行一次梯度下降
#在2.3.1的后半部分可以看到(例如公式2.6 2.7),求和符号没有了,此时用
#的是随机梯度下降,即计算一个样本就针对该样本进行一次梯度下降。
#两者的差异各有千秋,但较为常用的是随机梯度下降。
for i in range(m):
#获取当前样本的向量
xi = dataMat[i]
#获取当前样本所对应的标签
yi = labelMat[i]
#判断是否是误分类样本
#误分类样本特诊为: -yi(w*xi+b)>=0,详细可参考书中2.2.2小节
#在书的公式中写的是>0,实际上如果=0,说明改点在超平面上,也是不正确的
if -1 * yi * (w * xi.T + b) >= 0:
#对于误分类样本,进行梯度下降,更新w和b
w = w + h * yi * xi
b = b + h * yi
#打印训练进度
print('Round %d:%d training' % (k, iter))
#返回训练完的w、b
return w, b
def test(dataArr, labelArr, w, b):
'''
测试准确率
:param dataArr:测试集
:param labelArr: 测试集标签
:param w: 训练获得的权重w
:param b: 训练获得的偏置b
:return: 正确率
'''
print('start to test')
#将数据集转换为矩阵形式方便运算
dataMat = np.mat(dataArr)
#将label转换为矩阵并转置,详细信息参考上文perceptron中
#对于这部分的解说
labelMat = np.mat(labelArr).T
#获取测试数据集矩阵的大小
m, n = np.shape(dataMat)
#错误样本数计数
errorCnt = 0
#遍历所有测试样本
for i in range(m):
#获得单个样本向量
xi = dataMat[i]
#获得该样本标记
yi = labelMat[i]
#获得运算结果
result = -1 * yi * (w * xi.T + b)
#如果-yi(w*xi+b)>=0,说明该样本被误分类,错误样本数加一
if result >= 0: errorCnt += 1
#正确率 = 1 - (样本分类错误数 / 样本总数)
accruRate = 1 - (errorCnt / m)
#返回正确率
return accruRate
if __name__ == '__main__':
#获取当前时间
#在文末同样获取当前时间,两时间差即为程序运行时间
start = time.time()
#获取训练集及标签
trainData, trainLabel = loadData('../Mnist/mnist_train.csv')
#获取测试集及标签
testData, testLabel = loadData('../Mnist/mnist_test.csv')
#训练获得权重
w, b = perceptron(trainData, trainLabel, iter = 30)
#进行测试,获得正确率
accruRate = test(testData, testLabel, w, b)
#获取当前时间,作为结束时间
end = time.time()
#显示正确率
print('accuracy rate is:', accruRate)
#显示用时时长
print('time span:', end - start)
4 建模资料
资料分享: 最强建模资料