游戏开发中的噪声算法

一、噪声

噪声是游戏编程的常见技术，广泛应用于地形生成，图形学等多方面。

那么为什么要引入噪声这个概念呢？在程序中，我们经常使用直接使用最简单的rand()生成随机值，但它的问题在于生成的随机值太“随机”了，得到的值往往总是参差不齐，如下图使用随机值作为像素点的黑白程度：

而使用噪声，我们得到的值看起来虽然随机但平缓，这种图也看起来更自然和舒服：

1.1 随机性

随机性是噪声的基础，不必多说。

1.2 哈希性

在《Minecraft》里，由于世界是无限大的，它以“Chunk”区块（16×16×256格子）为单位，只加载玩家附近的区块。也就是说，当玩家在移动时，它会卸载远离的区块，然后加载靠近的区块。

一个问题是，当玩家离开一个区块时，进入第二个区块，然后又回到第一个区块，此时玩家期望看到的第一个区块和之前看到的保持一致。例如，输入1时得到0.3，输入2时得到0.7，当再次输入1时预期得到0.3。

因此噪声的一个重要性质是哈希性（可哈希的）。

尽管使用输入值作为srand()的参数来设置rand()的种子，从而达到哈希效果也是可行的。
然而最好花点时间写一个自己的哈希函数，使其简易使用而且也不破坏程序其他地方使用rand()的效果。

//一个随机性的哈希函数
unsigned int hash11(int position){
const unsigned int BIT_NOISE1 = 0x85297A4D;
const unsigned int BIT_NOISE2 = 0x68E31DA4;
const unsigned int BIT_NOISE3 = 0x1B56C4E9;
unsigned int mangled = position;
mangled *= BIT_NOISE1;
mangled ^= (mangled >> 8);
mangled += BIT_NOISE2;
mangled ^= (mangled << 8);
mangled *= BIT_NOISE3;
mangled ^= (mangled >> 8);
return mangled;
}

1.3 平滑性

对一个随机生成地形来说，如果简单的使用随机和哈希组合，
那么容易得到下图（以一维地图举例，x轴为位置，y轴为地形高度）：

容易看出的问题是，由于随机的杂乱无章，地形非常的参差不齐，这可不是一个自然的地形。

我们期望得到的地形不仅随机还应该是平滑的，这样才显得自然，如下图：

为了达到连续性，自然想到利用插值函数进行插值，常见的插值方法有：线性插值、缓和曲线插值

二、Value噪声

Value噪声是最简单的一种噪声，其主要思路是定义若干个顶点且每个顶点含有一个随机值（以顶点坐标作为参数通过哈希运算得到的），该随机值会周围坐标产生影响，越靠近顶点则越容易受该顶点影响（输出值越接近顶点随机值）。当需要求某个坐标的输出值时，需要将该坐标附近的各个顶点所造成的影响值进行叠加，从而得到一个总值并输出之。

原理：

1.首先定义一个晶格结构，每个晶格的顶点有一个伪随机值（Value）。对于二维的Value噪声来说，晶格结构就是一个平面网格（通常是正方形），三维的就是一个立体网格（通常是正方体）。

2.输入一个点（二维空间的话就是2D坐标），我们找到它所在晶格的顶点（二维下有4个，三维下有8个，N维下有 $2^n$ 个），并经过哈希运算得到这些顶点的伪随机值。

3.根据这些顶点的伪随机值，使用插值函数计算出输入点的输出值。对于插值函数的权重，我们还需要使用缓和曲线（ease curves）来计算这些伪随机值的权重和。在原始的Perlin噪声实现所使用的缓和曲线是 $s(t) = 3t^2 - 2t^3$ ，在2002年的论文中Perlin又改进为 $s(t) = 6t^5-15t^4+10t^3$ 。

实现：

int valueNoise(Vector2 p){
  //晶格以1为长度单位，通过向下取整可以确定p点所在晶格
  //注意：不应使用转变整型，因为负数的转整型是向上取整，而正数则是向下取整，这可能会导致(-1~0)和(0~1)的边缘问题
  Vector2 pi = Vector2(floor(p.x),floor(p.y));
  //找到对应晶格的四个顶点坐标
  Vector2 vertex[4] = {{pi.x,pi.y},{pi.x+1,pi.y},{pi.x,pi.y+1},{pi.x+1,pi.y+1}};
  //通过hash21函数得出坐标对应的随机值
  float vertexRandom[4] = {{hash21(vertex[0])},{hash21(vertex[1])},{hash21(vertex[2])},{hash21(vertex[3])}};  
  //wx、wy代表p点的权重，实际就是以(0.0~1.0)的范围表示在晶格中的位置比例
  float wx = (p.x-pi.x))/1.0f;
  float wy = (p.y-pi.y))/1.0f;
  //插值
  return interpolation(wx,wy,vertexRandom);
}

三、柏林噪声

谈起噪声，最著名的且最常用的莫过于Perlin噪声，Perlin噪声的名字来源于它的创始人Ken Perlin。

在理解了上面Value噪声后，我们再来看看柏林噪声的主要想法：
定义若干个顶点且每个顶点含有一个随机梯度向量，这些顶点会根据自己的梯度向量对周围坐标产生势能影响，沿着顶点的梯度方向越上升则势能越高。当需要求某个坐标的输出值时，需要将该坐标附近的各个顶点所造成的势能进行叠加，从而得到一个总势能并输出之。

我们给顶点赋予一个随机性的哈希函数，输入一个坐标可以得到一个随机向量，满足上述随机性和哈希性。
此外，由于势能是沿着梯度方向渐变的，所以很容易得到平滑性。

原理：

和Value噪声一样，它也是一种基于晶格的噪声，也需要三个步骤：

1.首先定义一个晶格结构，每个晶格的顶点有一个随机的梯度向量。对于二维的Perlin噪声来说，晶格结构就是一个平面网格（通常是正方形），三维的就是一个立体网格（通常是正方体）

2.输入一个点（二维空间的话就是2D坐标），我们找到它所在晶格的顶点（二维下有4个，三维下有8个，N维下有 $2^n$ 个），并经过哈希运算得到这些顶点的梯度向量（随机向量）；接着计算该点到各个晶格顶点的距离向量，再分别与顶点代表的梯度向量做点乘，得到 $2^n$ 个梯度值结果

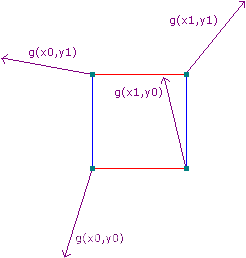
//点乘
float dot(Vector2 v1,Vector2 v2){
  return v1.x*v2.x+v1.y*v2.y;
}

//求梯度值（本质是求顶点代表的梯度向量与距离向量的点积）
float grad(Vector2 vertex, Vector2 p)
{
  return dot(hash22(vertex), p);
}

3.使用缓和曲线来计算它们的权重和（同样的，可以是 $s(t) = 3t^2 - 2t^3$ ，也可以是 $s(t) = 6t^5-15t^4+10t^3$

下图通过颜色差异显示了由2D柏林噪声生成的各像素点的值：

实现：

//二维柏林噪声
float perlinNoise(Vector2 p)
{  
  //向量两个纬度值向下取整
  Vector2 pi = Vector2(floor(p.x),floor(p.y));
  //找到对应晶格的四个顶点坐标
  Vector2 vertex[4] = {{pi.x,pi.y},{pi.x+1,pi.y},{pi.x,pi.y+1},{pi.x+1,pi.y+1}};
  //通过grad函数得出坐标对应的随机值
  float vertexRandom[4] = {grad(vertex[0],p),grad(vertex[1],p),grad(vertex[2],p),grad(vertex[3],p)};  
  //wx、wy代表p点的权重，实际就是以(0.0~1.0)的范围表示在晶格中的位置比例
  float wx = (p.x-pi.x))/1.0f;
  float wy = (p.y-pi.y))/1.0f;
  //插值
  return interpolation(wx,wy,vertexRandom);
}

gard函数另一个更快的实现方式，它与标准实现方式的区别是：晶体顶点是从若干个梯度向量里随机选择一个向量而不是产生一个随机向量，这样做可以预先计算好求梯度值时各项的系数。因此我们只需这样重写一下grad函数：

//求梯度值（本质是求顶点代表的梯度向量与距离向量的点积）
float grad(Vector2 vertex, Vector2 p)
{
    switch(hash21(vertex) % 4)
    {
      case 1: return  p.x + p.y;  //代表梯度向量(1,1)
      case 2: return -p.x + p.y;  //代表梯度向量(-1,1)
      case 3: return  p.x - p.y;  //代表梯度向量(1,-1)
      case 4: return -p.x - p.y;  //代表梯度向量(-1,-1)
      default: return 0; // never happens
    }
}

这里示例提供了4个可选的随机向量，实际上这个数量是偏少的，如果想要更加多样的效果，建议在实现时多提供些可选的随机向量。

四、Simplex噪声

Simplex噪声也是一种基于晶格的梯度噪声，它和Perlin噪声在实现上唯一不同的地方在于，它的晶格并不是方形（在2D下是正方形，在3D下是立方体，在更高纬度上我们称它们为超立方体，hypercube），而是单形（simplex）。

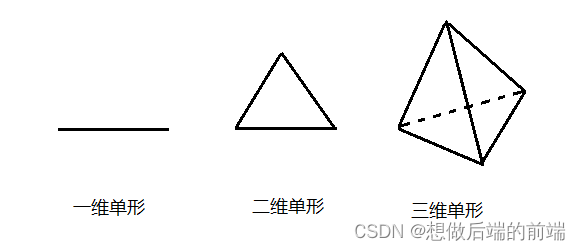
通俗解释单形的话，可以认为是在N维空间里，选出一个最简单最紧凑的多边形，让它可以平铺整个N维空间。我们可以很容易地想到一维空间下的单形是等长的线段，把这些线段收尾相连即可铺满整个一维空间。在二维空间下，单形是三角形，我们可以把等腰三角形连接起来铺满整个平面。三维空间下的单形就是四面体。更高维空间的单形也是存在的。

总结起来，在n维空间下，超立方体的顶点数目是 $2^n$ ，而单形的顶点数目是n+1，这使得我们在计算梯度噪声时可以大大减少需要计算的顶点权重数目。

一个潜在的问题是如何找到输入点所在的单形。
在计算Perlin噪声时，判断输入点所在的正方形是非常容易的，我们只需要对输入点下取整即可找到。
对于单形来说，我们需要对单形进行坐标偏斜（skewing），把平铺空间的单形变成一个新的网格结构，这个网格结构是由超立方体组成的，而每个超立方体又由一定数量的单形构成：

我们之前讲到的单形网格如上图中的红色网格所示，它们有一些等边三角形组成（注意到这些等边三角形是沿空间对角线排列的）。经过坐标倾斜后，它们变成了后面的黑色网格，这些网格由正方形组成，每个正方形是由之前两个等边三角形变形而来的三角形组成。这个把N维空间下的单形网格变形成新网格的公式如下：

$x' = x + (x+y+...)\cdot K1$

$y' = y + (x+y+...)\cdot K1$

其中， $K1 = \frac{\sqrt{n+1}-1}{n}$

在二维空间下，取n为2即可。这样变换之后，我们就可以按照之前方法判断该点所在的超立方体，在二维下即为正方形。

原理：

1.坐标偏斜：把输入点坐标进行坐标偏斜。

$x' = x + (x+y+...)\cdot K1$

$y' = y + (x+y+...)\cdot K1$

2.找到顶点：对偏斜后坐标下取整得到输入点所在的超立方体 $xi = floor(x'), yi = floor(y')$ ,...我们还可以得到小数部分 $xf = x'-xi, yf = y'-yi$ ,...我们把之前得到的(xf,yf,...)中的数值按降序排序，来决定输入点位于变形后的哪个单形内。这个单形的顶点是由按序排列的(0, 0, …, 0)到(1, 1, …, 1)中的n+1个顶点组成，共有n!种可能性。
我们可以按下面的过程来得到这n+1个顶点：从零坐标(0, 0, …, 0)开始，找到当前最大的分量，在该分量位置加1，直至添加了所有分量。这一步的算法复杂度即为排序复杂度 $O(n^2)$ 。

3.梯度选取：我们在偏斜后的超立方体网格上获取该单形的各个顶点的伪随机梯度向量。

4.变换回单形网格里的顶点：我们首先需要把单形顶点变回到之前由单形组成的单形网格。这一步需要使用第一步公式的逆函数来求得：

$x = x' + (x'+y'+...)\cdot K2$

$y = y' + (x'+y'+...)\cdot K2$

其中， $K2 = \frac{\frac{1}{\sqrt{n+1}}-1}{n}$

5.贡献度取和：我们由此可以得到输入点到这些单形顶点的位移向量。这些向量有两个用途，一个是为了和顶点梯度向量点乘，另一个是为了得到之前提到的距离值dist，来据此求得每个顶点对结果的贡献度：

$(r^2 - |dist|^2)^4 \times dot(dist,grad)$

实现：

float simplexNoise(Vector2 p)
{
  const float K1 = 0.366025404; // (sqrt(3)-1)/2;
  const float K2 = 0.211324865; // (3-sqrt(3))/6;
  //坐标偏斜
  float s = (p.X + p.Y) * K1;
  Vector2 pi = Vector2(floor(p.X+s),floor(p.Y+s));
  float t = (pi.X + pi.Y) *K2;
  Vector2 pf = p-(pi-t*Vector2::UnitVector);
  Vector2 vertex2Offset = (pf.X < pf.Y) ? Vector2(0, 1) : Vector2(1, 0);
  
  //顶点变换回单行网格空间
  Vector2 dist1 = pf;
  Vector2 dist2 = pf - vertex2Offset + K2 * Vector2::UnitVector;
  Vector2 dist3 = pf - Vector2(1,1) + 2 * K2 * Vector2::UnitVector;

  //计算贡献度取和
  float hx = 0.5f - Vector2::DotProduct(dist1, dist1);
  float hy = 0.5f - Vector2::DotProduct(dist2, dist2);
  float hz = 0.5f - Vector2::DotProduct(dist3, dist3);

  hx=hx*hx*hx*hx;
  hy=hy*hy*hy*hy;
  hz=hz*hz*hz*hz;

  //结果范围是[-1,1]
  return 70*(
  		hx*Vector2::DotProduct(dist1, hash22(pi)) 
	  	+hy*Vector2::DotProduct(dist2, hash22(pi + vertex2Offset))
	  	+hz*Vector2::DotProduct(dist3, hash22(pi + Vector2(1,1)))
      );
}

虽然理解上Simplex噪声相比于Perlin噪声更难理解，但由于它的效果更好、速度更优，因此很多情况下会替代Perlin噪声。

而且高维的噪声并不少见，例如对于常见的二维噪声纹理，我们可以额外引入时间分量，变成一个2D纹理动画（三维噪声），用于火焰纹理动画等..
对于常见的三维噪声纹理，引入额外的时间分量，就可以变成一个3D纹理动画（四维噪声），用于3D云雾动画等..
当我们需要一个可循环无缝衔接的动画时（见下文可平埔的噪声），那噪声又要提高一个维度。