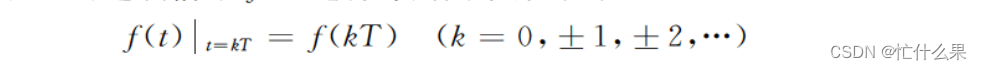文章目录
- 前言
- 参数估计的原理
- 总体、样本和统计量
- 点估计
- 区间估计
- 评价估计量的标准
- 有效性
- 总体均值的区间估计
- 一个总体均值的估计(大样本)
- 一个总体均值的估计(小样本估计)
- 练习
前言
本篇文章将开始介绍参数估计的相关知识。
参数估计的原理
总体、样本和统计量
在调查居民对延迟退休态度的例子中,每个爱民区居民的态度称为(这个调查问题中的)个体(element, individual, unit),而所有爱民区居民对这个问题的观点称为总体(population)
总体是包含所有要研究的个体的集合。
由于包含的个体数有限,该总体也称为有限总体(finite population)
如果总体包含的个体数是无限或相对无限的,则称为无限总体(infinite population)
调查获得的部分爱民区居民的观点(也就是部分个体)称为该总体的一个样本(sample),它是从总体中选出的一部分。
总体代表我们所关心的那部分现实世界
在大多数情况下,要么总体的规模很大,要么很难确定总体的所有成员,因此需要通过样本信息来推断总体特征
但是,样本虽然含有总体的信息,但是信息一般比较分散,不能直接用于统计推断
为了把分散在样本中的信息集中起来,我们用样本的某个不含总体未知参数的函数来表示,这个函数就称为统计量(statistics)
因此,统计量是对数据的压缩
如果样本的函数包含了未知参数,那这个函数就不是统计量,因为还未完成对数据的压缩。
如果能够估计出参数,那么对总体的具体分布就知道得差不多了。换句话说,不知道总体的特征参数,但可以通过计算样本统计量来估计总体参数。
用于估计参数的统计量称为估计量(estimator)。若得到一组观察值,则将其代入估计量得到的具体数值, 称为参数的估计值。
今后,将不再强调估计量和估计值的区别,在不至于引起混淆的场合统称为估计。
点估计
点估计(point estimation)是用估计量 的某个取值直接作为总体参数θ的估计值。比如:用样本均值 直接作为总体均值μ的估计值;
用样本比例p直接作为总体比例的估计值,等等。
比如:从软件行业从业人员中抽出一个随机样本,计算出平均月收入为18000元,用18000元作为该行业从业人员月平均收入的一个估计值,这就是点估计。
比如:要估计一批产品的合格率,根据样本计算的合格率为98%,将98%直接作为这批产品合格率的估计值,这也是点估计。
由于点估计无法得到估计的可靠性(因为一个点估计量的可靠性是由其抽样分布的标准误来衡量的),也无法说出点估计值与总体参数真实值接近的程度,因此,我们不能完全依赖一个点估计,而应围绕点估计值构造出总体参数的一个区间。
区间估计
区间估计(interval estimate)是在点估计的基础上,给出总体参数估计的一个估计区间,该区间由样本统计量加减估计误差而得到。
根据样本统计量的抽样分布能够对样本统计量与总体参数的接近程度给出一个概率度量。
比如,某班级平均分数在75~85之间,置信水平是95% 。
在区间估计中,由样本估计量构造出的总体参数在一定置信水平下的估计区间称为置信区间(confidence interval,CI),其中区间的最小值称为置信下限,最大值称为置信上限。
置信区间中包含总体参数真值的次数所占的比例称为置信水平,也称为置信度或置信系数(confidence coefficient)。统计上,常用的置信水平有90%,95%和99%。有关置信区间的概念可用下面的图来表示:
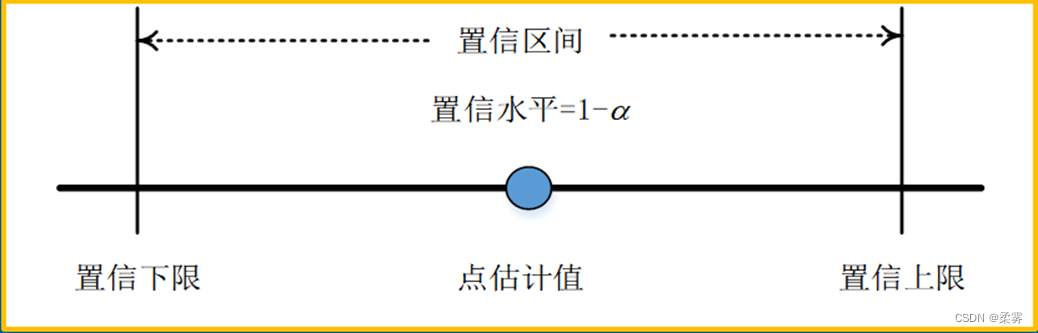
对于固定的样本量,置信水平越大,包含总体均值的区间就越多(上下比较)
对于同样的置信水平,样本量n大的, 区间往往就短些(左右比较)
在每个图内部的各个置信区间的长短也不一样,因为样本标准差因样本 而异,这也影响了置信区间的宽度。
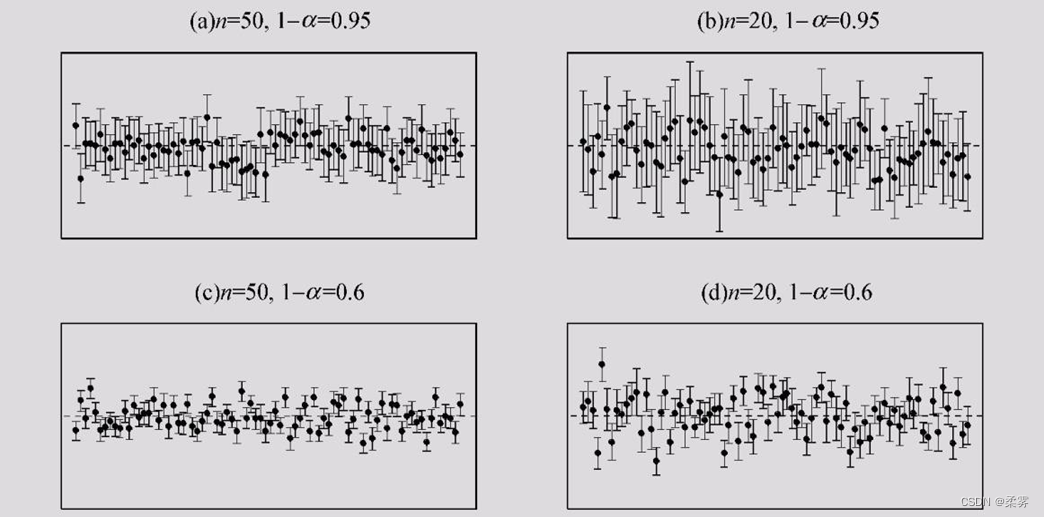
样本量相同时,置信水平越大,置信区间就越宽。置信水平相同时,样本量越大,置信区间就越窄。
使用一个较大的置信水平会得到一个比较宽的置信区间,而使用一个较大的样本则会得到一个较准确(较窄)的区间。直观地说,较宽的区间会有更大的可能性包含参数
但实际应用中,过宽的区间往往没有实际意义。
区间估计的两个端点都是统计量,因而也都是随机变量
“某总体参数μ的置信度为100 1− 𝜶 %的置信区间”意味着如果抽取(相同样本量)的大量样本,那么,从这些样本中 得到的以同样方法(或公式)计算的大量区间中会有大约𝟏− 𝜶比例的区间包含未知的总体参数𝝁,而有约𝜶比例的区间不包含该总体参数
具体的从一个样本中计算出来的一个数值区间,比如前面的(75,85),则要么包含真实比例,要么不包含真实比例。
由于真实比例和这个区间(75,85)都是确定的数,不包括随机性,也没有概率可言。因此,“95%置信区间(75,85)以概率0.95包含真实比例”的说法是正确的还是错误的?
该种说法是错误的。
评价估计量的标准
用于估计总体参数θ的估计量 可以有很多。
如:可以用样本均值作为总体均值的估计量
也可以用样本中位数作为总体均值的估计量,等等。
那么,究竟用哪种估计量作为总体参数的估计呢?什么样的估计量才算是一个好的估计量呢?这就需要有一定的评价标准。统计学家给出了评价估计量的一些标准,主要有以下几个。
无偏性、有效性、一致性。

无偏性(unbiasedness)是指估计量抽样分布的数学期望等于被估计的总体参数。设总体参数为 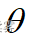 ,所选择的估计量为
,所选择的估计量为  ,如果
,如果 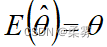 ,则称
,则称 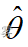 是
是 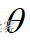 的无偏估计量。
的无偏估计量。
由统计量的抽样分布可知,E( )=μ,E(p)=π,E( )= ,因此 、p、 分别是总体均值μ、总体比例、总体方差的无偏估计量。
样本均值、样本中位数和样本方差的无偏性模拟
假定从均值为50、方差为100的正态总体中随机抽取10000组样本量为10的样本,分别计算出10000个样本均值的均值样本中位数的均值和样本方差的均值
注:函数vector()用于产生一个空向量。函数append(x, values, after = length(x))在向量x中追加数值,after指定在哪个数据后插入数值。
x<-vector();m<-vector();v<-vector()
n=10
for(i in 1:10000){
x<-append(x,mean(rnorm(n,50,10)))
m<-append(m,median(rnorm(n,50,10)))
v<-append(v,var(rnorm(n,50,10)))
}
data.frame(mean(x),mean(m),mean(v))

在正态总体条件下,样本均值和样本中位数都是总体均值的无偏估计量,而样本方差则是总体方差的无偏估计量。


有效性
无偏性对估计量而言是很基本的要求,它的直观意义是没有系统误差。
一个好的估计量应当对参数的平均偏差比较小。
第二个标准就是无偏估计量中取方差最小的估计量,也称为最有效或者最好的估计量。换句话说,这就是当样本变化时,该统计量变化最小
方差小,说明由许多样本产生的各个估计量之间差别较小 。

衡量估计量好坏的第三个标准是一致性或相合性 (consistency)
它意味着样本量越大,估计量对总体参数的估计就越精确(统计量收敛于所估总体的参数)
当样本容量越大时,信息越多,当然估计就应该越准确
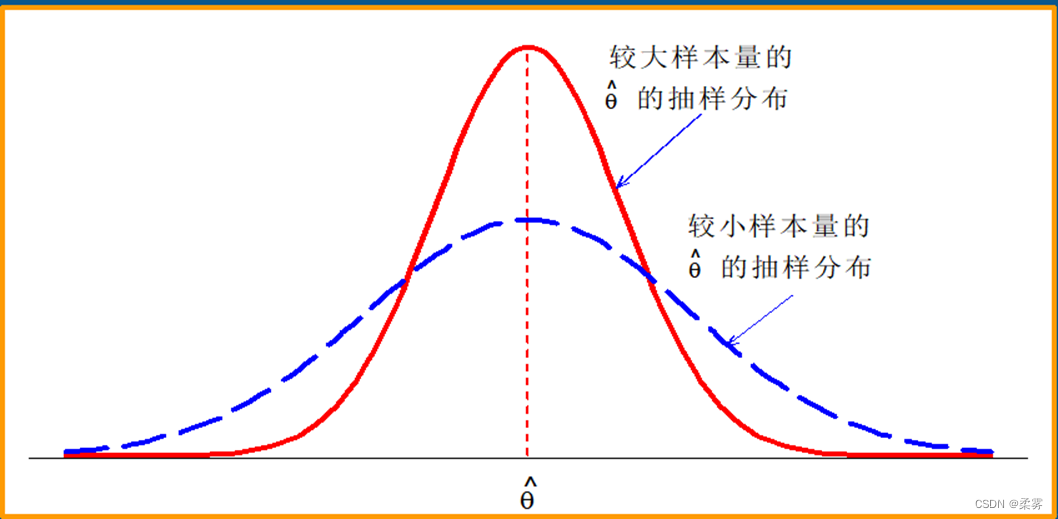
假定总体是均值为50、方差为100的1000正态随机数,从该总体分别抽取样本量为10,100,500,900的样本,并计算出每个样本的均值:
计算样本量分别为10、100、500、900时的样本均值
N=rnorm(1000,50,10)
mu=mean(N)
xbar10<-mean(sample(N,10,replace=F))
xbar100<-mean(sample(N,100,replace=F))
xbar500<-mean(sample(N,500,replace=F))
xbar900<-mean(sample(N,900,replace=F))
data.frame(总体均值=mu,xbar10,xbar100,xbar500,xbar900)

计算样本均值与总体均值mu的差值d
data.frame("d10"=(xbar10-mu),"d100"=(xbar100-mu),"d500"=(xbar500-mu),"d900"=(xbar900-mu))

样本均值随着样本量的增大而越来越接近总体均值。
总体均值的区间估计
一个总体均值的估计(大样本)
一个总体均值区间的一般表达式:
总体均值的置信区间是由样本均值加减估计误差得到的
估计误差由两部分组成:一是点估计量的标准误,它取决于样本统计量的抽样分布。二是估计时所要的求置信水平,统计量分布两侧面积对应的分位数值,它取决于事先所要求的可靠程度
总体均值在置信水平下的置信区间可一般性地表达为
样本均值±分位数×样本均值的标准误。
在大样本(n≥30)情形下,由中心极限定理可知,样本均值近似服从期望值为μ、方差为 的正态分布。
使用正态分布统计量 z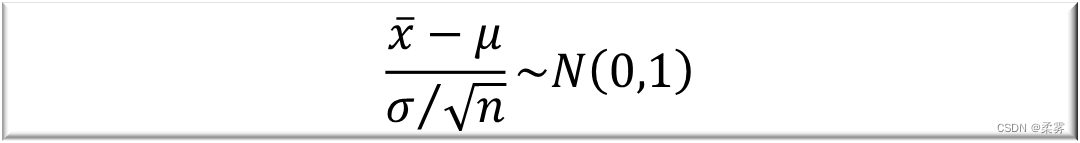
总体均值 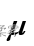 在1-
在1-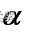 置信水平下的置信区间为
置信水平下的置信区间为

是事先确定的一个概率值,它是总体均值不包括在置信区间内的概率;
(1- 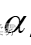 )称为置信水平;
)称为置信水平;
 是标准正态分布两侧面积各为
是标准正态分布两侧面积各为 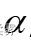 /2时的z值;
/2时的z值;
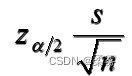 是估计误差。
是估计误差。
可以看出:
置信区间的上下界是统计量,因此该区间是随机区间。
从上面的推导可以看出, 置信度是该随机区间覆盖真实均值的概率。
如果根据一个样本的数据算出上下界的实现值,就不是随机区间了,而是一个固定的数值区间。
例题:
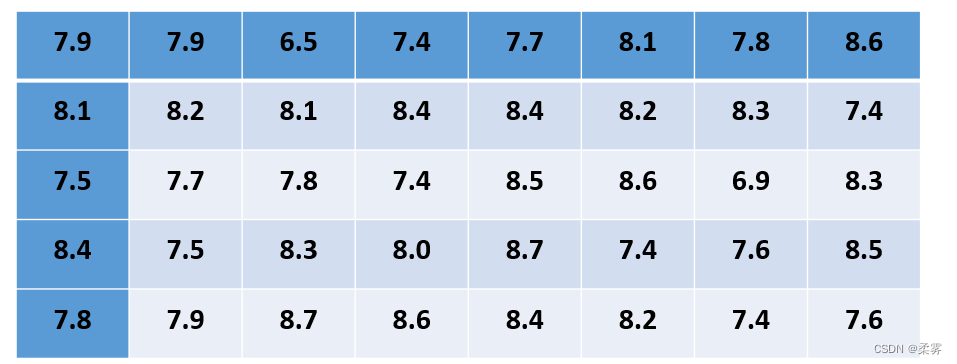
一家研究机构随机抽取40辆相同排气量的家用轿车,经过测试得到每百公里耗油量数据(单位:升) 。建立该排气量轿车平均耗油量的90%的置信区间
example5_1
注:函数z.test(x,y=NULL,sigma.x=NULL,sima.y=NULL,conf. level=0.95)用于构建基于标准正态分布的单样本和双样本的置信区间和假设检验。参数y=NULL用于单样本; sigma.x和 sigma.y用于指定两个总体的标准差,当总体标准差未知时用样本标准差代替;conf.level用于指定置信水平,默认为0.95.
平均耗油量的90%的置信区间(使用z.test函数)
load("C:/example/ch5/example5_1.RData")
library(BSDA)
z.test(example5_1$耗油量,sigma.x=sd(example5_1$耗油量),conf.level=0.90)

只输出置信区间的信息
z.test(example5_1
耗油量
,
s
i
g
m
a
.
x
=
s
d
(
e
x
a
m
p
l
e
5
1
耗油量,sigma.x=sd(example5_1
耗油量,sigma.x=sd(example51耗油量),conf.level=0.90)$conf.int
一个总体均值的估计(小样本估计)
假定条件(对总体均值的估计)
总体服从正态分布
小样本 (n < 30)
如果正态总体的σ已知,样本均值经过标准化后仍然服从标准正态分布,此时可使用 建立总体均值的置信区间
如果正态总体的σ未知,样本均值经过标准化后则服从自由度为n-1的t分布,此时使用 t 分布统计量
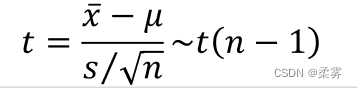
总体均值 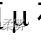 在1-
在1- 置信水平下的置信区间为
置信水平下的置信区间为
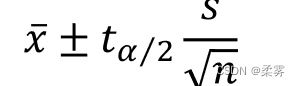
例题:
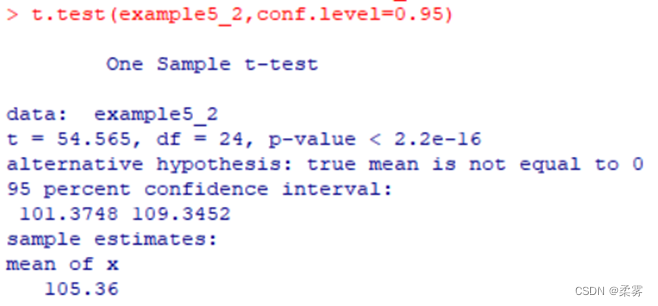
(数据:example5_2.Rdata)从一批袋装食品中随机抽取25袋,测得每袋重量如下表所示。假定食品重量服从正态分布,估计该批食品平均重量的置信区间,置信水平为95%。
总体服从正态分布但σ未知,由于是小样本,样本均值经标准化后服从自由度为n-1的t分布。

注:t.test(x,y=NULL,mu=0, paired=FALSE,var.equal=FALSE)用于单样本和双样本假设检验。参数y=NULL用于单样本;独立样本时, paired=FALSE;方差不等时,var equal=FALSE。
食品平均重量95%的置信区间(使用t.test函数)
load("C:/example/ch5/example5_2.RData")
t.test(example5_2,conf.level=0.95)
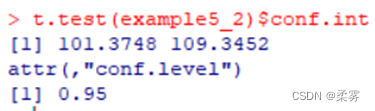
只输出置信区间的信息
t.test(example5_2)$conf.int
练习
1、假定从均值为0、方差为1的正态总体中随机抽取10000组样本量为10的样本,如何来计算出10000个样本均值的方差和样本中位数的方差?从结果当中我们又能得到什么结论?
x<-vector();m<-vector()
n=10
for(i in 1:10000){
x<-append(x,mean(rnorm(n)))
m<-append(m,median(rnorm(n)))
}
data.frame(var(x),var(m))
2、某快餐店想要估计每位顾客午餐平均花费的金额,在为期3周的时间里选取49名顾客组成了一个简单随机样本,得到样本均值为120元,标准差为15元。求总体均值μ的95%的置信区间。
用公式计算
q<-qnorm(0.975)
LCI<-120-q*(15/sqrt(49))
UCI<-120+q*(15/sqrt(49))
data.frame(LCI,UCI)
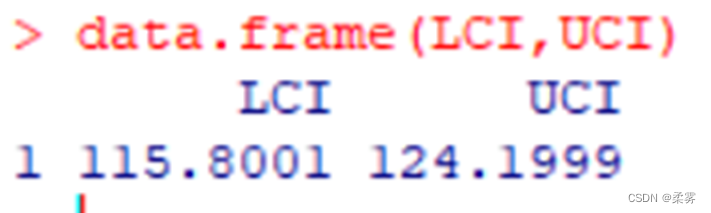
3、利用下面的信息,构建总体均值μ的置信区间。
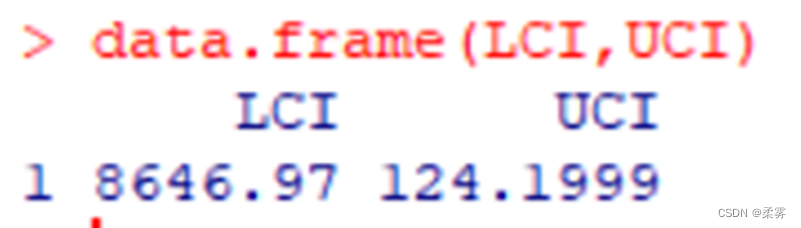
(1)总体服从正态分布,已知σ=500,n=15, =8900,置信水平为95%。
用公式计算

q<-qnorm(0.975)
LCI<-8900-q*(500/sqrt(15))
UCL<-8900+q*(500/sqrt(15))
data.frame(LCI,UCI)



![[Error]连接iPhone调试时提示Failed to prepare the device for development.](https://img-blog.csdnimg.cn/direct/8faa77347a35461b84c12294f506be30.png)