题目
在一个字符串 S 中,如果 Si=Si−1 且 Si≠Si+1,则称 Si和 Si+1 为边缘字符。
如果 Si≠Si−1 且 Si=Si+1,则 Si−1 和 Si 也称为边缘字符。
其它的字符都不是边缘字符。
对于一个给定的串 S,一次操作可以一次性删除该串中的所有边缘字符(操作后可能产生新的边缘字符)。
请问经过 264264 次操作后,字符串 S 变成了怎样的字符串,如果结果为空则输出 EMPTY。
输入格式
输入一行包含一个字符串 S。
输出格式
输出一行包含一个字符串表示答案,如果结果为空则输出 EMPTY。
数据范围
对于 25% 的评测用例,|S|≤10^3,其中 |S|表示 S 的长度;
对于 50% 的评测用例,|S|≤10^4;
对于 75% 的评测用例,|S|≤10^5;
对于所有评测用例,|S|≤10^6,S 中仅含小写字母。
样例
输入样例1
edda
输出样例1
EMPTY
输入样例2
sdfhhhhcvhhxcxnnnnshh
输出样例2
s题目思路
该题目的重点在于如何对其进行优化。从题目中可以清楚的看出,如果我们使用暴力做法的话会TLE,如果每一次只删除一个字符,那么时间复杂度:n、n-1、n-2、n-3……1.;如此时间复杂度为O(n^2),在这题中最多能过50%的数据。
优化只要添加一个备选数,在备选数中去查找边缘数。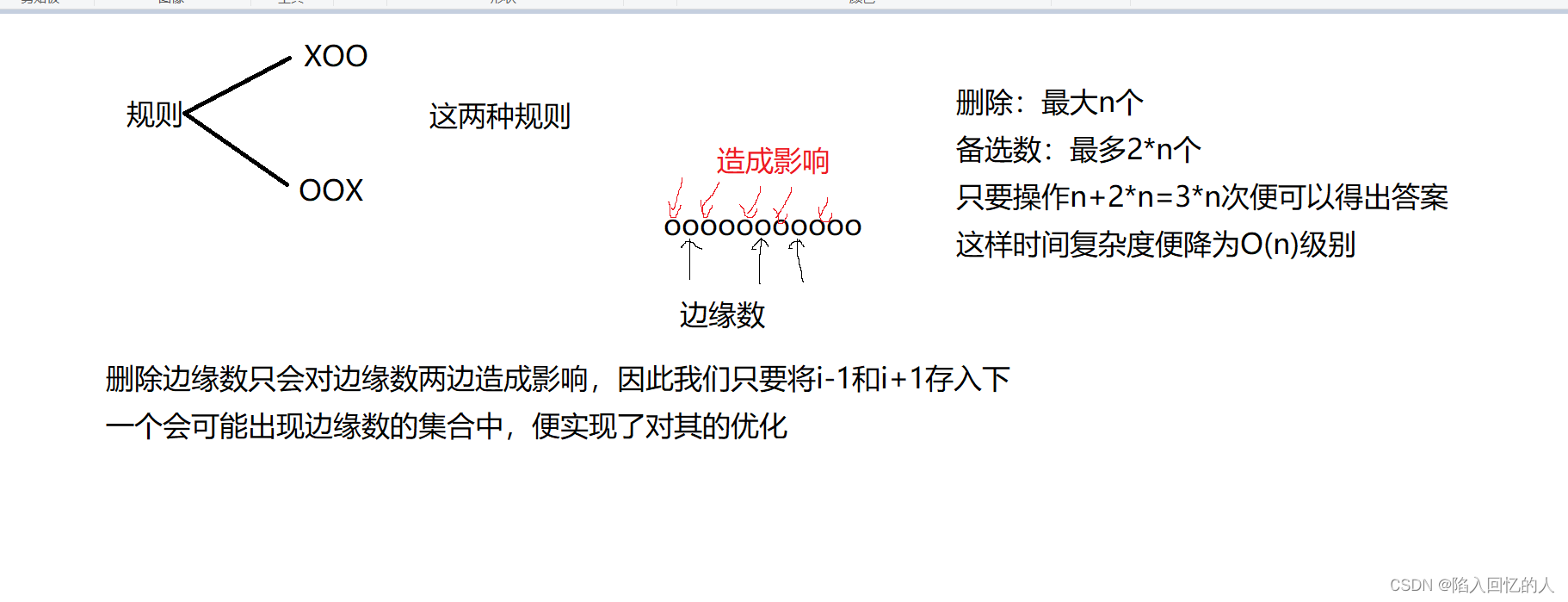
源代码
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e6+10;
char g[N];
int l[N],r[N];
vector<int> q,w;
bool st[N];
int n;
void insert(int k){
if(!st[k]){
st[k]=true;
w.push_back(k);
}
}
void filter_dels(){
w.clear();
for(int k:q){
int a=l[k],b=k,c=r[k];
if(g[a]==g[b] && g[b]!=g[c] && g[c]!='*'){
insert(b);
insert(c);
}
if(g[c]==g[b] && g[b]!=g[a] && g[a]!='*'){
insert(b);
insert(a);
}
}
}
int main()
{
scanf("%s",g+1);
n=strlen(g+1);
g[0]=g[n+1]='*';
for(int i=1;i<=n;i++){
q.push_back(i);
l[i]=i-1,r[i]=i+1;
}
r[0]=1,l[n+1]=n;
while(true){
filter_dels();
if(w.empty()) break;
q.clear();
for(int k:w){
int a=l[k],b=k,c=r[k];
//q.back()!=a这个条件保证了不会出现备选数,当然如果删除也是可以的
//如:xxoo其中中间两个xo被添加了两次,如果不加条件的话
if (!st[a] && a && (q.empty() || q.back()!=a)) q.push_back(a);
if (!st[c] && c != n + 1) q.push_back(c);
//删除k节点
r[a]=c,l[c]=a;
}
}
if(r[0]==n+1) puts("EMPTY");
else{
for(int i=r[0];i!=n+1;i=r[i]) printf("%c",g[i]);
}
return 0;
}没有优化的代码——这个代码只能过33.3%的数据
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 1e6+10;
char g[N];
int l[N],r[N];
queue<int> q;
bool st[N];
int n;
//查找边缘字符,只要记录前一个节点即可
void insert(int x){
if(x==1 || x==n) return;
int left=l[x],right=r[x];
if(g[left]!=g[x] && g[right]==g[x]) q.push(left),q.push(x);
else if(g[right]!=g[x] && g[left]==g[x]) q.push(x),q.push(right);
}
void deletes(int x){
l[r[x]]=l[x];
r[l[x]]=r[x];
}
int main()
{
scanf("%s", g+1);
n=strlen(g+1);
g[0]=g[n+1]='*';;
for(int i=1;i<=n;i++){
l[i]=i-1,r[i]=i+1;
}
r[0]=1,l[n+1]=n;
while(true){
for(int i=r[0];i!=n+1;i=r[i]) insert(i);
if(q.empty()) break;
while(!q.empty()){
auto x=q.front();
q.pop();
if(!st[x]) deletes(x);
st[x]=true;
}
}
if(r[0]==n+1) puts("EMPTY");
else{
for(int i=r[0];i!=n+1;i=r[i]) printf("%c",g[i]);
}
return 0;
}