·本节展示了计算机中的加法器和比较器的底层实现电路设计。

加法器

        计算机中加法器的实现依赖门的结构，如果是两个十进制进行加减，则首先把右边的两个0-9之间的数相加，它们的总和在0-18之间，如果答案是0-9之间，则直接写在两个数下面，如果答案在10-18之间，则写下右边的数字，然后把1加在左边的下一列。

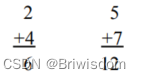
        在二进制数系统中，实际上要简单的多。当两个二进制数做加法时候，右边的两列数字只能是0或者1,。因此将两个二进制数字的右列相加的唯一可能答案是0、1或10（零、一或二）。如果你加0+0，你得到0、1+0或0+1，你得到1，1+1，你在右边的列中得到0，在左边的列中携带1。

        我们前面介绍的异或门，与门可以实现这个加法器。两个输入连接的XOR将告诉我们右边列的答案应该是什么，两位的and将告诉我们是否需要将1加到左边列。如果一位为开，另一位为关，也就是说，我们将1和0相加，右列的答案将为1。如果两个数字都为1，或者两个数字均为0，则右列将为0。与门仅在两个输入数字均为1的情况下开启。

        当要加上第三个数字时候，同理用如下门结构来实现：

        左边的XOR告诉我们“a”和“b”是否不同。如果它们是，并且“进位”是关闭的，或者如果“a”和“b”是相同的，并且“入位”是打开的，那么右XOR将生成1作为当前列的总和。如果两个输入都打开，则下与门将打开“进位”。如果“进位输入”和其中一个输入都开启，则上与门将开启“进位输出”。这就是计算机加法的简单方式！现在我们看到了它的工作原理，我们可以对它做一个更简单的描述。

        要制作一个将两个字节相加的加法器，我们需要一个一位加法器来处理字节的每一位，每个位的进位输出连接到下一位的进进位输入。请注意，每一位都有进位，即使是第一位（右列）。当我们想加上大于255的数字时，也会用到这个。

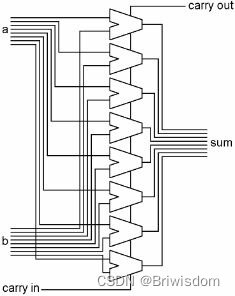
        简化版本如下：

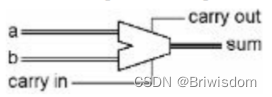
        如果两个数字之和大于255，则最左边（顶部）列的进位输出位将打开，该位将在计算机的其他位置使用。这就是计算机做加法的方式。

比较器

        比较器只产生两个输出：是否相等，a是否更大。我们希望比较器做的是找出输入总线上的两个字节是否完全相等，如果不相等，根据二进制数系统，“a”总线上的字节是否更大。

        同样的事情很简单。当输入相同时，XOR门关闭，因此如果所有XOR门都关闭，则输入相等。要确定两个二进制数中较大的一个有点棘手。你必须从两个最高位开始，如果一个是开的，另一个是关的，那么开的那个是更大的数字。如果它们是相同的，那么你必须检查下一对较低的比特等，直到你找到一对不同的比特。但是一旦你找到了一对不同的，你就不想再检查任何比特了。例如，0010 0000（32）大于0001 1111（31）。前两位在两个字节中相同。第三位在第一个字节中打开，在第二个字节中关闭，因此第一个字节更大。尽管其余的位在第二个字节中打开，但它们的总数小于第一个字节中的一位。

        一个字节是8位，所以要想实现比较器，需要五个门结构和八个bit位置。从两个字节的高bit位开始，用XOR传递比较结果。

        左侧的a,b来自总线上的一个bit， 右边c是输出到总线上的一个bit。如果门1的输出打开，则意味着“a”和“b”不同或不相等。我们添加门2，当“a”和“b”相等时，门2将打开。

        如果门2在每个位置都打开，那么门3也将在每个位置打开，从底部出来的位告诉我们两个输入字节相等。

        如果如下三件事属实，4号门就会打开。1） 位“a”和“b”不同。2） 位“a”是打开的位。3）高于此点的所有位都相等。当门4打开时，它打开门5，并且在该点以下每隔一个门5打开，因此比较器的输出“更大”。

        当字节“b”是较大的一个时，“相等”位和“较大”位都将关闭。您将这些位比较器中的八个堆叠起来，如下图所示，其中一个“1”和“0”连接到最上面的一个以启动它。“c”处仍然有XOR函数，现在底部有两个比较器位。

        再次简化，我们将回到总线型XOR图，只需添加比较器的两个新输出位

        在我们的计算机里还有一件我们需要的东西，它给我们提供了另一点信息。这是一个简单的门组合，以一个完整的字节作为输入，只生成一位作为输出。当字节中的所有位都关闭时，输出位打开。

        它只是一个八输入或门和一个非门。当或门的任何一个输入都打开时，其输出将打开，非门的输出将关闭。只有当或门所有八个输入都关闭，其输出因此关闭时，非门输出才会打开。更简单的总线表示如右图所示。