目录
参考链接
定义
直观理解
公式推导
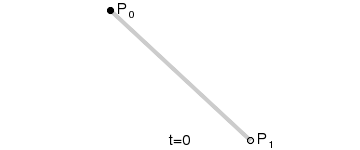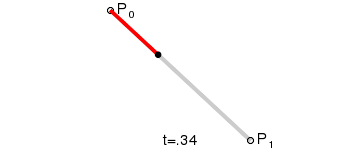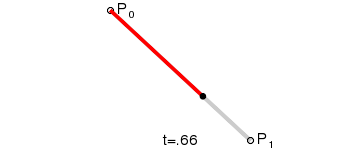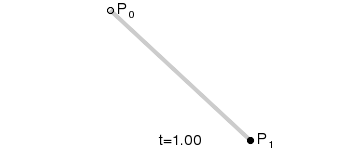
一次贝塞尔曲线(线性公式)
二次贝塞尔曲线(二次方公式)
三次贝塞尔曲线(三次方公式)
n次贝塞尔曲线(一般参数公式)
代码实现
参考链接
贝塞尔曲线(Bezier Curve)原理及公式推导_bezier曲线-CSDN博客
贝塞尔曲线(Bezier Curve)原理、公式推导及matlab代码实现-CSDN博客
贝塞尔曲线——这个是可以在线控制点来绘制贝塞尔曲线的网站
定义
贝塞尔曲线用于计算机图形绘制形状,CSS 动画和许多其他地方。
贝塞尔曲线(Bezier curve),又称贝兹曲线或贝济埃曲线,是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线,贝兹曲线定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。 贝塞尔曲线是计算机图形学中相当重要的参数曲线,在一些比较成熟的位图软件中也有贝塞尔曲线工具,如PhotoShop等。
1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名,称为贝塞尔曲线。
贝塞尔曲线的一些特性:
- 使用
个控制点
来控制曲线的形状
- 曲线通过起始点
和终止点
,接近但不通过中间点
-
曲线的阶次等于控制点的数量减一。 对于两个点我们能得到一条线性曲线(直线),三个点 — 一条二阶曲线,四个点 — 一条三阶曲线。
-
曲线总是在控制点的凸包内部:
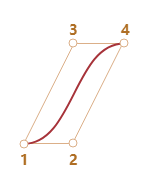

由于最后一个属性,在计算机图形学中,可以优化相交测试。如果凸包不相交,则曲线也不相交。因此,首先检查凸包的交叉点可以非常快地给出“无交叉”结果。检查交叉区域或凸包更容易,因为它们是矩形,三角形等(见上图),比曲线简单的多。
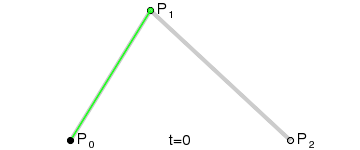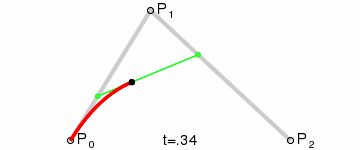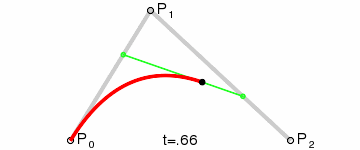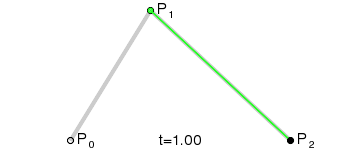
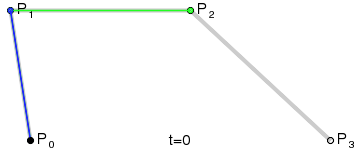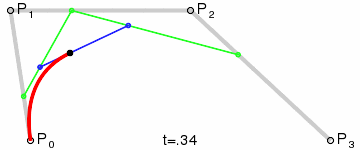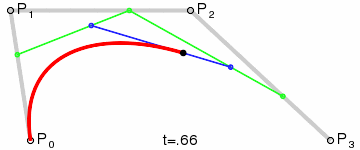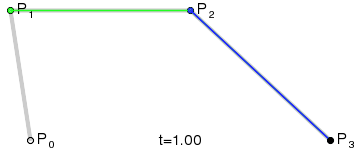
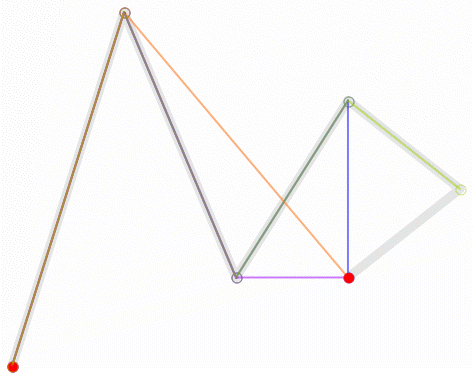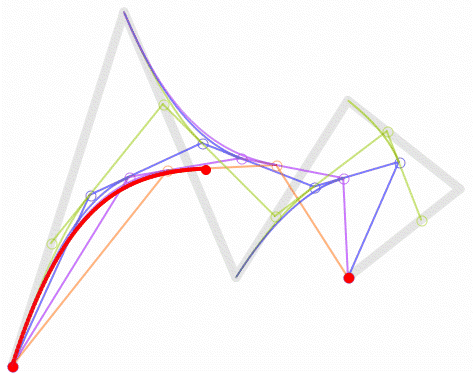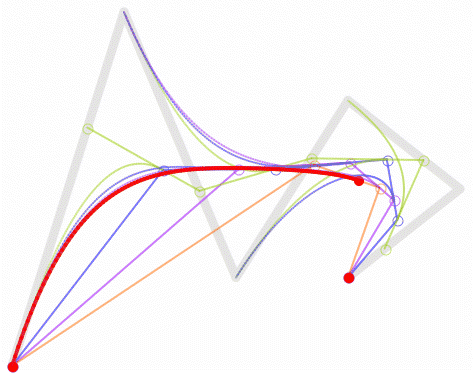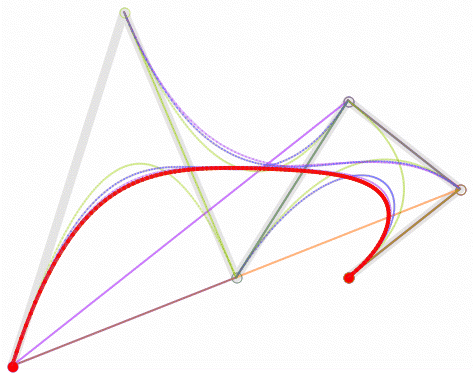
直观理解
Step 1. 在二维平面内选三个不同的点并依次用线段连接
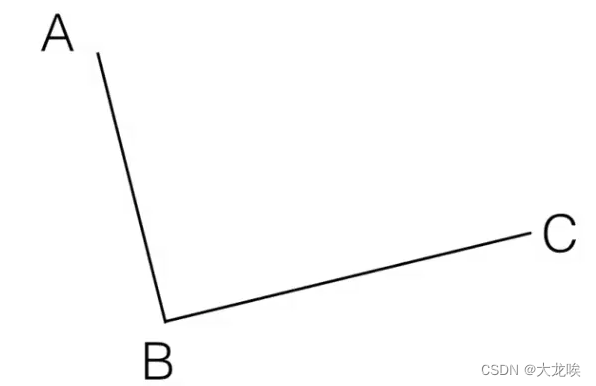
Step 2. 在线段和
上找到
、
两点,使得
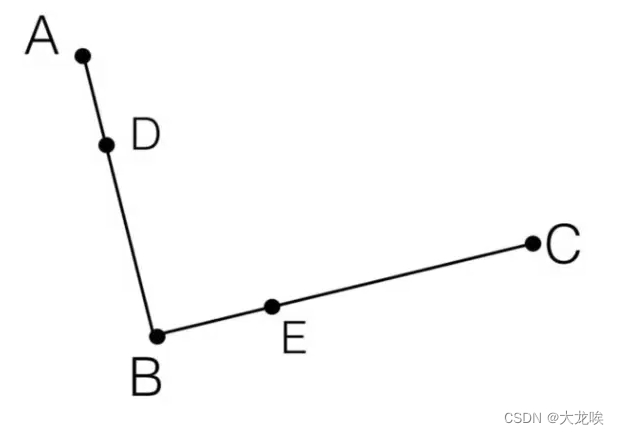
Step 3. 连接,并在
上找到
点,使其满足
(抛物线的三切线定理)
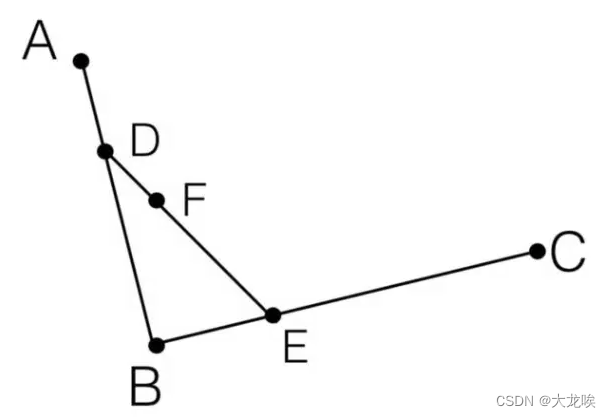
Step 4. 找出符合上述条件的所有点

上述为一个二阶贝塞尔曲线。同样的有阶贝塞尔曲线:
| 曲线 | 图示 |
| 一阶 |
|
| 二阶 |
|
| 三阶 |
|
| 四阶 |
|
| 五阶 |
|
公式推导
一次贝塞尔曲线(线性公式)
定义:给定点
、
,线性贝塞尔曲线只是一条两点之间的直线,这条线由下式给出,且其等同于线性插值:

其中,公式里的、
同步表示为其
或
轴坐标。
假设坐标为
,
坐标为
,
坐标为
,则有:
同理有:
于是可将上式简写为:
二次贝塞尔曲线(二次方公式)
定义:二次贝塞尔曲线的路径由给定点
、
、
的函数
给出:
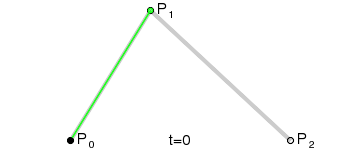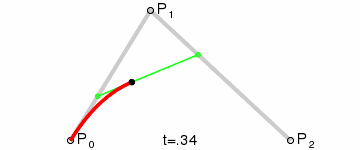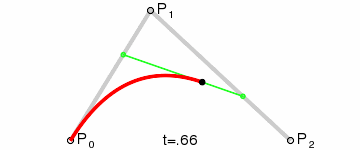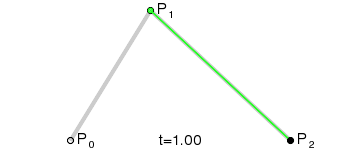
假设、
上的点为
,
、
上的点为
,
上的点为
(也即
为曲线上的点。则根据一次贝塞尔曲线公式有:
将上式中、
带入
中,即可得到二次贝塞尔曲线的公式:
三次贝塞尔曲线(三次方公式)
同理可得三次贝塞尔曲线公式:
n次贝塞尔曲线(一般参数公式)
定义:给定点
、
、
,则
次贝塞尔曲线由下式给出:
n次贝塞尔曲线的公式可由如下递归表达:
进一步可以得到贝塞尔曲线的递推计算公式:
代码实现
首先来看不同阶数的贝塞尔曲线公式,来找共同点:
N=2:
N=3:
N=4:
可将贝塞尔曲线一般参数公式中的表达式用如下方式表示:
设有常数 a,b 和 c,则该表达式可统一表示为如下形式:
根据上面的分析就可以总结出 a,b,c 对应的取值规则:
b: 递减到 0 (b 为 1-t 的幂)
c: 0 递增到 (N - 1) (c 为 t 的幂)
a: 在 N 分别为 1,2,3,4,5 时将其值用如下形式表示:
N=1:---------1
N=2:--------1 1
N=3:------1 2 1
N=4:-----1 3 3 1
N=5:---1 4 6 4 1
a 值的改变规则为: 杨辉三角
-------------------------------------------------------------------
理论基础有了,开始写代码
a 值用杨辉三角计算,b ,c 值在for 循环里计算,从传入的点坐标读取。
step1:首先使用杨辉三角的方式生成a值
N = len(control_points)
ta = np.zeros((N, N))
# 初始化杨辉三角左右两边的值为1
for i in range(N):
ta[i, 0] = 1
ta[i, i] = 1
# 计算杨辉三角
for row in range(2, N):
for col in range(1, row):
ta[row, col] = ta[row-1, col-1] + ta[row-1, col]step2:生成贝塞尔曲线上的点
p = np.zeros((M, 2))
for i in range(M):
t = i / M # 确定每一个点的比例
for k in range(N):
c = k # 分别确定 a, b, c 三个系数
b = N - c - 1 # 分别确定 a, b, c 三个系数
a = ta[N-1, k] # 分别确定 a, b, c 三个系数
# 确定点的 x 和 y 坐标
p[i, 0] += a * (1 - t)**b * t**c * control_points[k, 0]
p[i, 1] += a * (1 - t)**b * t**c * control_points[k, 1]
完整代码
# N表示控制点个数,M表示时间步
import numpy as np
from scipy.special import comb
def calculate_bezier_curve(control_points, M=1000):
N = len(control_points)
ta = np.zeros((N, N))
# 初始化杨辉三角左右两边的值为1
for i in range(N):
ta[i, 0] = 1
ta[i, i] = 1
# 计算杨辉三角
for row in range(2, N):
for col in range(1, row):
ta[row, col] = ta[row-1, col-1] + ta[row-1, col]
p = np.zeros((M, 2))
for i in range(M):
t = i / M # 确定每一个点的比例
for k in range(N):
c = k # 分别确定 a, b, c 三个系数
b = N - c - 1 # 分别确定 a, b, c 三个系数
a = ta[N-1, k] # 分别确定 a, b, c 三个系数
# 确定点的 x 和 y 坐标
p[i, 0] += a * (1 - t)**b * t**c * control_points[k, 0]
p[i, 1] += a * (1 - t)**b * t**c * control_points[k, 1]
return p
# 示例调用
control_points = np.array([(0, 0), (1, 2), (2, 0)])
result_points = calculate_bezier_curve(control_points)
# 打印结果
print(result_points)
# 可视化
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 6))
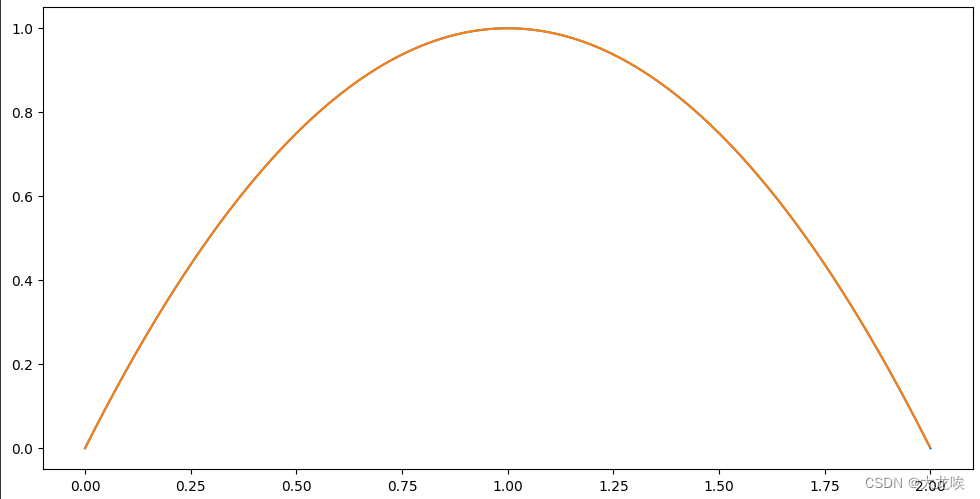
plt.plot(result_points[:, 0], result_points[:, 1], label='Bezier Curve')下图是一个生成的二阶贝塞尔曲线(有3个控制点)
另外一种实现方式:
def bezier_curve(points, n_times=1000):
"""
Generate a Bezier curve from control points.
Args:
points (list of tuples): control points.
n_times (int): number of time steps (resolution of the curve).
Returns:
list of tuples: points on the bezier curve.
"""
n_points = len(points)
t = np.linspace(0, 1, n_times)
curve = np.zeros((n_times, 2))
for i in range(n_points):
binom = comb(n_points - 1, i) # 计算二项式系数,即组合数。表示从 n_points - 1 个元素中选择 i 个元素的方式有多少种。
curve += np.outer(binom * (t ** i) * ((1 - t) ** (n_points - 1 - i)), points[i])
return curve
control_points1 = [(0, 0), (1, 2), (2, 0)]
bezier1 = bezier_curve(control_points1)
print(bezier1)