NOIP2011提高组day1 - T3：Mayan游戏（玛雅游戏）

题目链接

[NOIP2011 提高组] Mayan 游戏

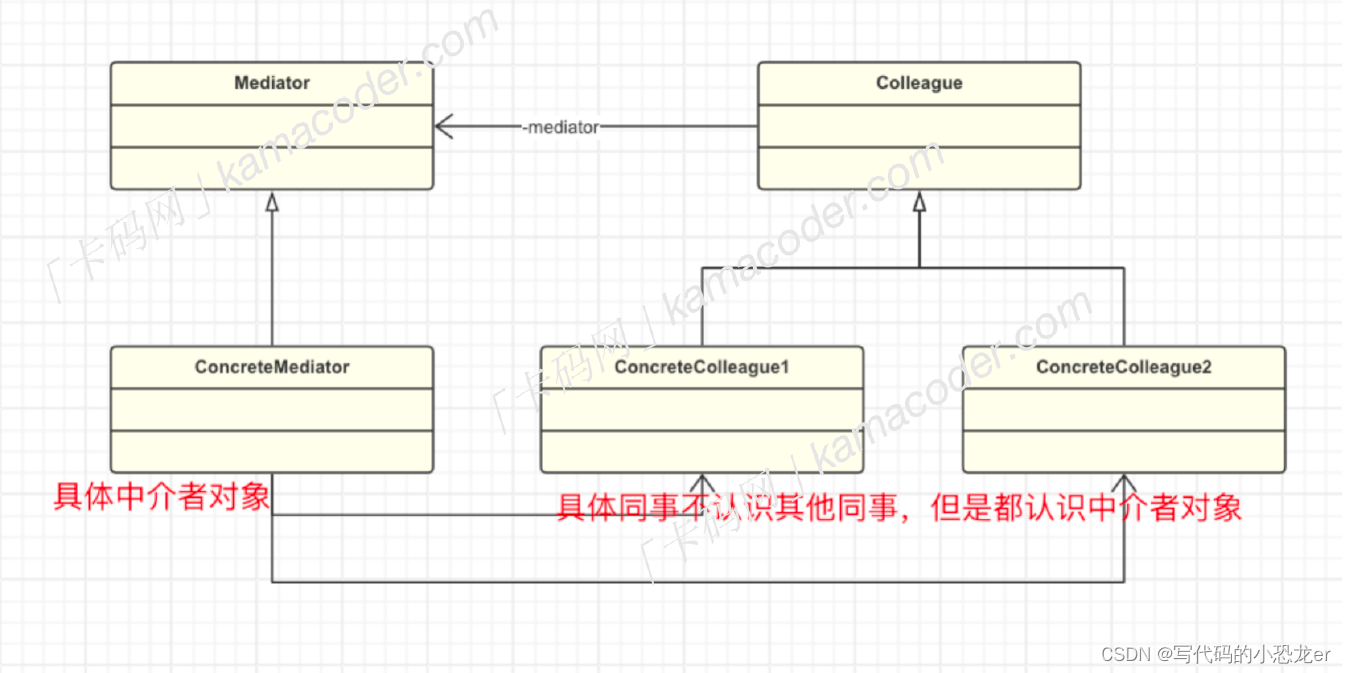
题目描述

Mayan puzzle 是最近流行起来的一个游戏。游戏界面是一个 $7$ 行 $\times5$ 列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见输入输出样例说明中的图 $6$ 到图 $7$ ）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见下面图 $1$ 和图 $2$ ）；

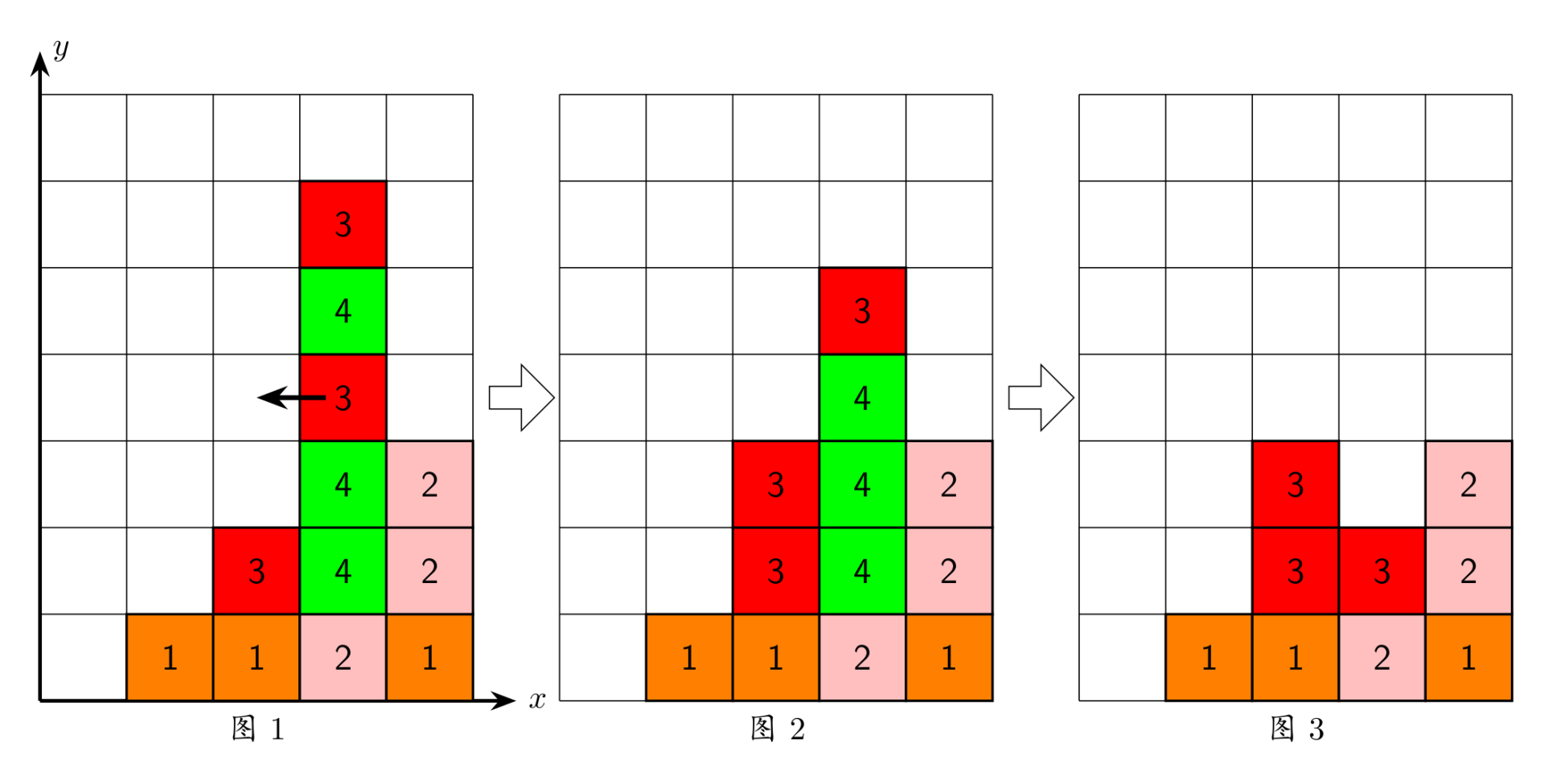
任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1 到图3）。

注意：

a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图 $4$ ，三个颜色为 $1$ 的方块和三个颜色为 $2$ 的方块会同时被消除，最后剩下一个颜色为 $2$ 的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5 所示的情形， $5$ 个方块会同时被消除）。

方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图 $1$ 到图 $3$ 给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为 $(0, 0)$ ，将位于 $(3, 3)$ 的方块向左移动之后，游戏界面从图 $1$ 变成图 $2$ 所示的状态，此时在一竖列上有连续三块颜色为 $4$ 的方块，满足消除条件，消除连续 $3$ 块颜色为 $4$ 的方块后，上方的颜色为 $3$ 的方块掉落，形成图 $3$ 所示的局面。

输入格式

共 $6$ 行。

第一行为一个正整数 $n$ ，表示要求游戏通关的步数。

接下来的 $5$ 行，描述 $\times 5$ 的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个 $0$ 结束，自下向上表示每竖列方块的颜色编号（颜色不多于 $10$ 种，从 $1$ 开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

输出格式

如果有解决方案，输出 $n$ 行，每行包含 $3$ 个整数 $x, y, g$ ，表示一次移动，每两个整数之间用一个空格隔开，其中 $(x, y)$ 表示要移动的方块的坐标， $g$ 表示移动的方向， $1$ 表示向右移动， $- 1$ 表示向左移动。注意：多组解时，按照 $x$ 为第一关键字， $y$ 为第二关键字， $1$ 优先于 $- 1$ ，给出一组字典序最小的解。游戏界面左下角的坐标为 $(0, 0)$ 。

如果没有解决方案，输出一行 -1。

样例 #1

样例输入 #1

样例输出 #1

2 1 1
3 1 1
3 0 1

提示

【输入输出样例说明】

按箭头方向的顺序分别为图 $6$ 到图 $11$

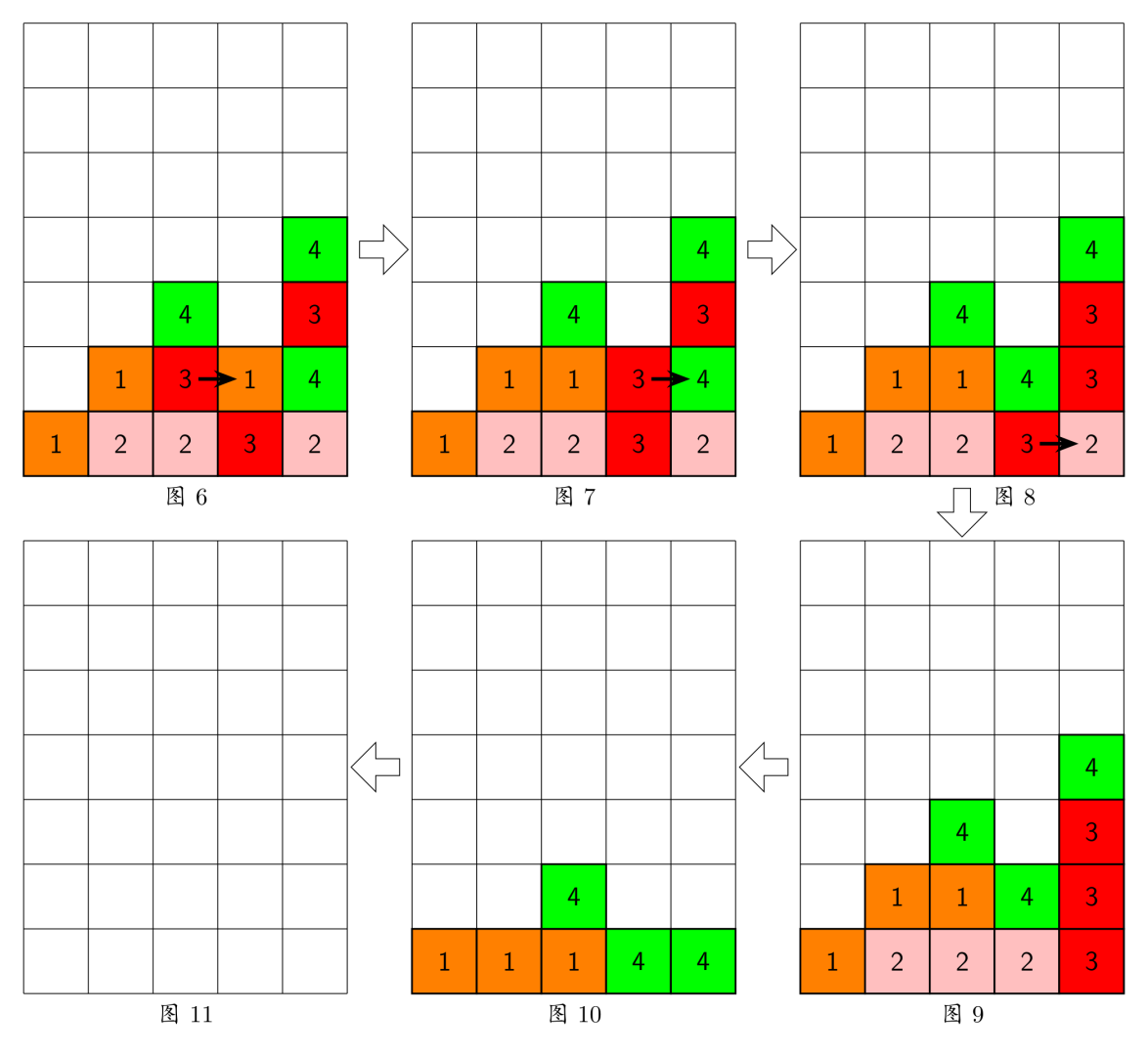
样例输入的游戏局面如上面第一个图片所示，依次移动的三步是： $(2, 1)$ 处的方格向右移动， $(3, 1)$ 处的方格向右移动， $(3, 0)$ 处的方格向右移动，最后可以将棋盘上所有方块消除。

【数据范围】

对于 $30\%$ 的数据，初始棋盘上的方块都在棋盘的最下面一行；

对于 $100\%$ 的数据， $\le 5$ 。

算法思想

根据题目描述，可以分析出下面一些有用的信息。

方块的移动规则：
- 每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格
- 当拖动这一方块时，如果拖动后到达的位置也有方块，那么这两个方块将交换位置
- 如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落，直到不悬空
方块的消除规则：
- 如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除
- 如果同时有多组方块满足消除条件，几组方块会同时被消除
- 如果行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除
方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除

由于题目给出的数据范围比较小，游戏通关的步数 $\le 5$ ，也就是最多枚举 $5$ 步得到解决方案，因此直接暴力搜索每一步移动的方块，模拟移动和消除的过程即可。

搜索顺序

依次枚举每一步选择哪个方块，向左右哪个方向移动。

可行性剪枝

当某种颜色的方块数量小于等于 $2$ 时，无法消除，则一定无解，直接剪枝。

优化性剪枝

根据输出要求，多组解时，按照 $x$ 为第一关键字， $y$ 为第二关键字， $1$ 优先于 $- 1$ ，给出一组字典序最小的解。其中 $1$ 表示向右移动， $- 1$ 表示向左移动。

如果将有颜色的方块 $(i, j)$ 向左移动时，而左侧方块 $(i - 1, j)$ 也有颜色，则不如将左边的方块向右移动，即 $j)\to(i, j)$ ，这样得到的字典序更小。因此在这种情况下，应该进行最优性剪枝。

移动和消除

当选择将 $a$ 列 $b$ 行的方块移动 $c$ 列 $b$ 行时，即 $b)\to(c, b)$ ：

首先将这两个方块将交换位置
其次要重复下面几个步骤，直到没有方块被消除为止：
- 处理悬空方块，即被移走或者消除的方块上面的方块要落下来。
- 检查行列上是否有符合消除规则的方块，将其标记为消除
- 消除方块

时间复杂度

总共有 $5\times7=35$ 个方块，每个格子可以向左或向右移动，一共移动 $5$ 步，也就是说最坏情况下每一步都有 $70$ 种选择，时间复杂度为 $O(70^5)$ 。

但随着方块被消除，以及剪枝操作，实际搜索的空间远小于最坏情况。

代码实现

#include <iostream>
#include <cstring>
using namespace std;
struct S {
    int x, y, d; //记录移动过程
}ans[5];
int n;
int g[5][7], bg[5][5][7]; //bg备份数组，用于回溯恢复现场
int cnt[15], bcnt[5][15]; //cnt[i]表示第i种颜色的方块数量
bool st[5][7]; //用来标记方块是否被消除
void move(int a, int b, int c)
{
    swap(g[a][b], g[c][b]); //交换两个方块
    while(true) //一直处理直到没有消除方块
    {
        for(int i = 0; i < 5; i ++) //处理悬空方块
        {
            int k = 0;
            for(int j = 0; j < 7; j ++) //有颜色的方块向下移动
                if(g[i][j]) g[i][k ++] = g[i][j];
            while(k < 7) g[i][k ++] = 0; //将k上方的方块都设置为0
        }
        
        memset(st, 0, sizeof st);
        bool flag = false; //是否消除了方块
        //消除方块
        for(int i = 0; i < 5; i ++)
            for(int j = 0; j < 7; j ++)
            {
                if(g[i][j])
                {
                    int L = i, R = i; //计算方块(i,j)左右相同颜色方块的数量
                    while(L - 1 >= 0 && g[L - 1][j] == g[i][j]) L --;
                    while(R + 1 < 5 && g[R + 1][j] == g[i][j]) R ++;
                    if(R - L + 1 >= 3) //可以消除
                    {
                        st[i][j] = true; //标记成消除状态
                        flag = true;
                    }
                    else //不能消除则继续检查同一列是否能消除
                    {
                        int D = j, U = j; //计算方块(i,j)上下相同颜色方块的数量
                        while(D - 1 >= 0 && g[i][D - 1] == g[i][j]) D --;
                        while(U + 1 < 7 && g[i][U + 1] == g[i][j]) U ++; //注意这里小于7行
                        if(U - D + 1 >= 3)
                        {
                            st[i][j] = true;
                            flag = true;
                        }
                    }
                    
                }
            }
        if(!flag) break;
        for(int i = 0; i < 5; i ++)
            for(int j = 0; j < 7; j ++)
                if(st[i][j]) //消除格子
                {
                    cnt[0] --;
                    cnt[g[i][j]] --;
                    g[i][j] = 0;
                }
    }
}

bool dfs(int u)
{
    if(u == n) return cnt[0] == 0; //搜索结束，如果方块全部消除则有解
    
    for(int i = 1; i <= 10; i ++) //可行性剪枝，当某种颜色的方块数量小于等于2时，无法消除，则一定无解
        if(cnt[i] == 1 || cnt[i] == 2)
            return false;
    
    memcpy(bg[u], g, sizeof g); //备份，用来恢复现场
    memcpy(bcnt[u], cnt, sizeof cnt); 
    //选择1个方块进行移动
    for(int i = 0; i < 5; i ++)
        for(int j = 0; j < 7; j ++)
            if(g[i][j]) //有方块
            {
                int c = i + 1; //向右移动
                if(c < 5)
                {
                    ans[u] = {i, j, 1};
                    move(i, j, c);
                    if(dfs(u + 1)) return true;
                    memcpy(g, bg[u], sizeof g); //回溯，恢复现场
                    memcpy(cnt, bcnt[u], sizeof cnt);
                }
                c = i - 1; //向左移动
                if(c >= 0 && g[c][j] == 0) //向左移动，而左边方块也有颜色，进行最优性剪枝
                {
                    ans[u] = {i, j, -1};
                    move(i, j, c);
                    if(dfs(u + 1)) return true;
                    memcpy(g, bg[u], sizeof g); //回溯，恢复现场
                    memcpy(cnt, bcnt[u], sizeof cnt);
                }
            }
    return false;
}
int main()
{
    scanf("%d", &n);
    for(int i = 0; i < 5; i ++) //枚举列
    {
        int c, j = 0; //j表示行
        while(scanf("%d", &c), c != 0)
        {
            g[i][j ++] = c;
            cnt[0] ++; //方块的总数
            cnt[c] ++; //c颜色的方块数量
        }
    }
    if(dfs(0)) //从第0步暴力搜索
    {
        for(int i = 0; i < n; i ++)
            printf("%d %d %d\n", ans[i].x, ans[i].y, ans[i].d);
    }
    else puts("-1");
    return 0;
}