C++ 二叉树OJ题

news2024/9/28 17:29:21

目录

1、606. 根据二叉树创建字符串

2、102. 二叉树的层序遍历 

3、107. 二叉树的层序遍历 II

4、236. 二叉树的最近公共祖先

5、JZ36 二叉搜索树与双向链表

6、105. 从前序与中序遍历序列构造二叉树

7、106. 从中序与后序遍历序列构造二叉树

8、144. 二叉树的前序遍历

9、94. 二叉树的中序遍历

10、145. 二叉树的后序遍历

1、606. 根据二叉树创建字符串

思路：

  1. 首先判断当前节点是否为空，为空则返回空字符串，不为空则将节点的值转换成字符串，并将其赋值给str。
  2. 接着判断如果节点的左右子节点至少有一个不为空，将左括号添加到str中，然后递归调tree2str函数处理左子树，并将结果添加到str中，最后添加右括号。接着检查当前节点是否有右子节点。
  3. 如果有右子节点，表示当前节点无论是否有左子节点和右子节点，都需要添加括号。
class Solution {
public:
    string tree2str(TreeNode* root) {
        if (root == nullptr)
            return "";
        string str = to_string(root->val);
        if (root->left || root->right) {
            str += '(';
            str += tree2str(root->left);
            str += ')';
        }
        if (root->right) {
            str += '(';
            str += tree2str(root->right);
            str += ')';
        }
        return str;
    }
};

拓展： 

在C++中，std::stoi函数是一个非常有用的函数，它可以将字符串转换为整数。类似的，我们还有std::stol，std::stoll，std::stof，std::stod，std::stold等函数，它们分别用于将字符串转换为长整型，长长整型，浮点型，双精度浮点型和长双精度浮点型。

#include <string>
#include <iostream>

int main() {
    std::string str1 = "42";
    std::string str2 = "3.14159";
    std::string str3 = "1234567890123456789";
    std::string str4 = "0x7f";

    int num1 = std::stoi(str1);
    float num2 = std::stof(str2);
    long long num3 = std::stoll(str3);
    int num4 = std::stoi(str4, 0, 16); // 使用16进制

    std::cout << "num1: " << num1 << "\n";
    std::cout << "num2: " << num2 << "\n";
    std::cout << "num3: " << num3 << "\n";
    std::cout << "num4: " << num4 << "\n";

    return 0;
}

在这个例子中，我们首先定义了四个字符串，然后使用不同的函数将它们转换为不同类型的数字。注意，std::stoi和std::stoll等函数的第二个和第三个参数是可选的，它们分别用于指定转换的基数（例如，10表示十进制，16表示十六进制）和存储转换停止的位置。 

std::stoi(str4, 0, 16)时出现的0实际上是第三个参数，它表示转换的基数。这个例子中，基数被设置为0，这意味着函数会根据字符串的格式自动确定基数。

输出：

num1: 42
num2: 3.14159
num3: 1234567890123456789
num4: 127

to_string函数：to_string函数用于将数字转换为字符串。它接受一个数字作为参数，并返回相应的字符串表示。这个函数对于将数字与其他字符串连接起来或者在输出中使用数字非常有用。

#include <iostream>
#include <string>

int main() {
    int num = 12345;
    std::string str = std::to_string(num);
    std::cout << "Converted string: " << str << std::endl;
    return 0;
}

 输出：

Converted string: 12345

2、102. 二叉树的层序遍历 

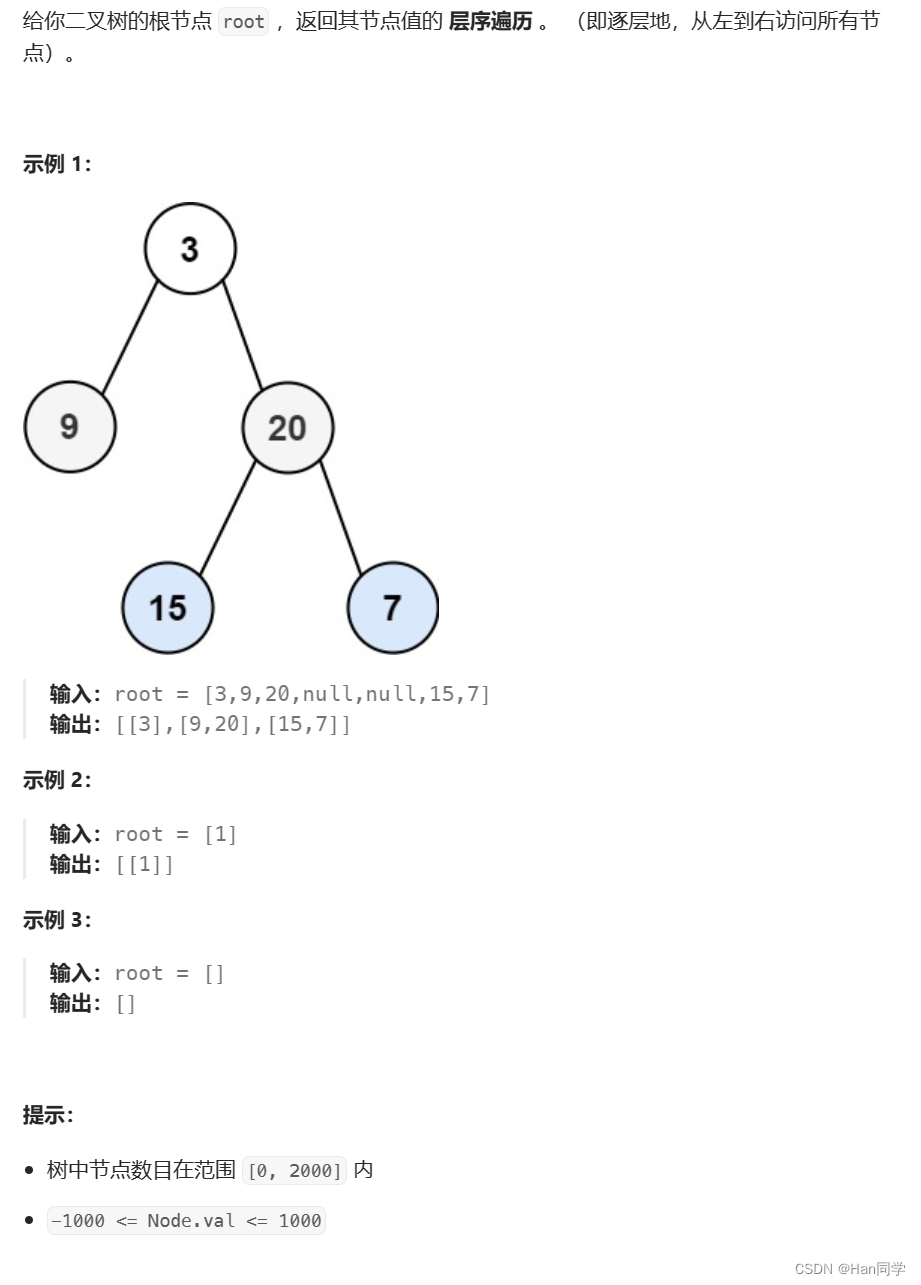
思路：使用队列来实现层序遍历，每次遍历一层的节点，并将节点的值存储在一个二维向量中返回。 

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        int levelSize = 0;
        if (root) {
            q.push(root);
            levelSize = 1;
        }
        vector<vector<int>> vv;
        while (!q.empty()) {
            vector<int> v;
            while (levelSize--) {
                TreeNode* front = q.front();
                q.pop();
                v.push_back(front->val);
                if (front->left)
                    q.push(front->left);
                if (front->right)
                    q.push(front->right);
            }
            vv.push_back(v);
            levelSize = q.size();
        }
        return vv;
    }
};

  1. 首先定义了一个Solution类，其中包含了一个levelOrder函数，用于执行层序遍历操作。

  2. 在levelOrder函数中，创建了一个队列q，用于存储待遍历的节点。同时，定义了一个变量levelSize，用于记录当前层的节点数量。

  3. 如果根节点root存在，将其加入队列q，并将levelSize设置为1。

  4. 创建一个二维向量vv，用于存储遍历结果。

  5. 进入while循环，当队列q不为空时，执行以下操作：

    a. 创建一个一维向量v，用于存储当前层的节点值。

    b. 在内层while循环中，通过levelSize--来遍历当前层的节点。每次循环，从队列q中取出一个节点front，并将其值加入到v中。

    c. 如果front的左子节点存在，将其加入队列q。

    d. 如果front的右子节点存在，将其加入队列q。

    e. 将v加入到vv中，表示当前层的节点值已经遍历完毕。

    f. 将levelSize更新为队列q的大小，即下一层的节点数量。

  6. 循环结束后，返回二维向量vv，即为二叉树的层序遍历结果。

3、107. 二叉树的层序遍历 II

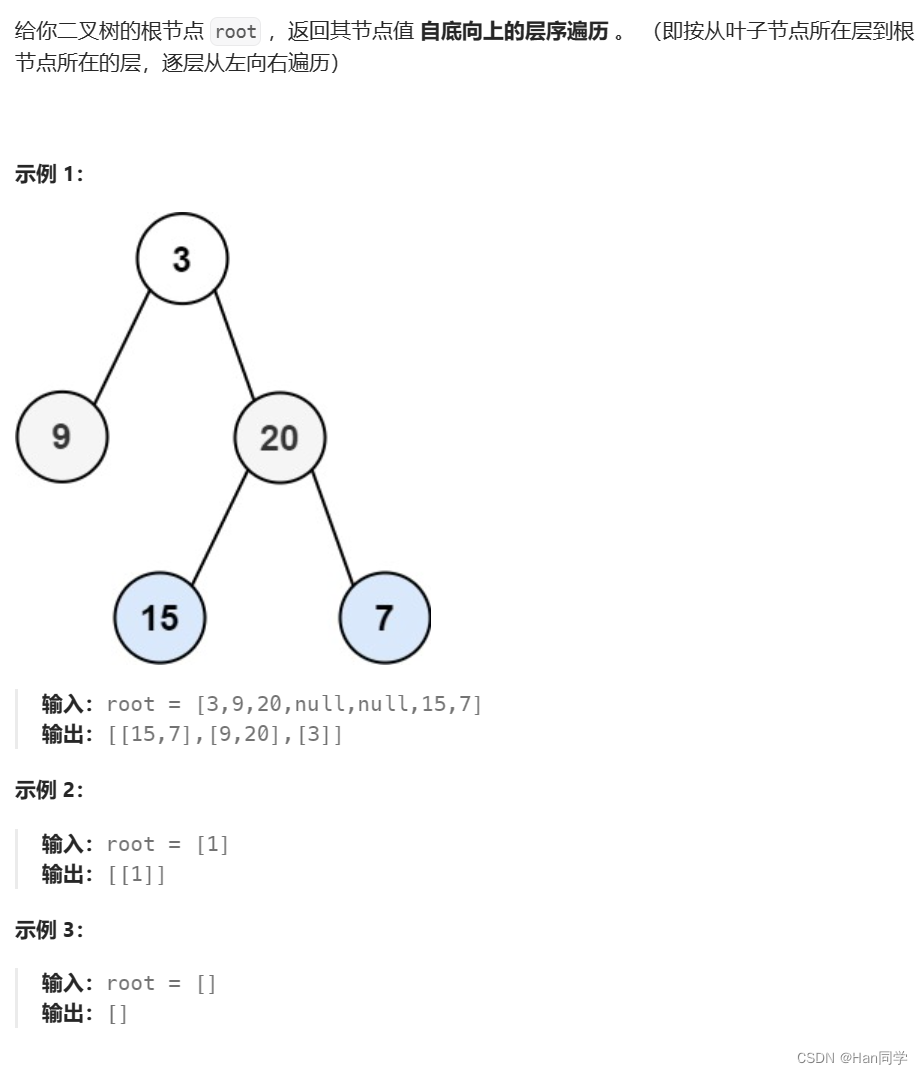
思路：与上题思路一样，仅需将结果数组逆置即可。 

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        queue<TreeNode*> q;
        int levelSize = 0;
        vector<vector<int>> vv;
        if (root) {
            q.push(root);
            levelSize = 1;
        }
        while (!q.empty()) {
            vector<int> v;
            while (levelSize--) {
                TreeNode* front = q.front();
                q.pop();
                v.push_back(front->val);
                if (front->left)
                    q.push(front->left);
                if (front->right)
                    q.push(front->right);
            }
            vv.push_back(v);
            levelSize = q.size();
        }
        reverse(vv.begin(), vv.end());
        return vv;
    }
};

 

4、236. 二叉树的最近公共祖先

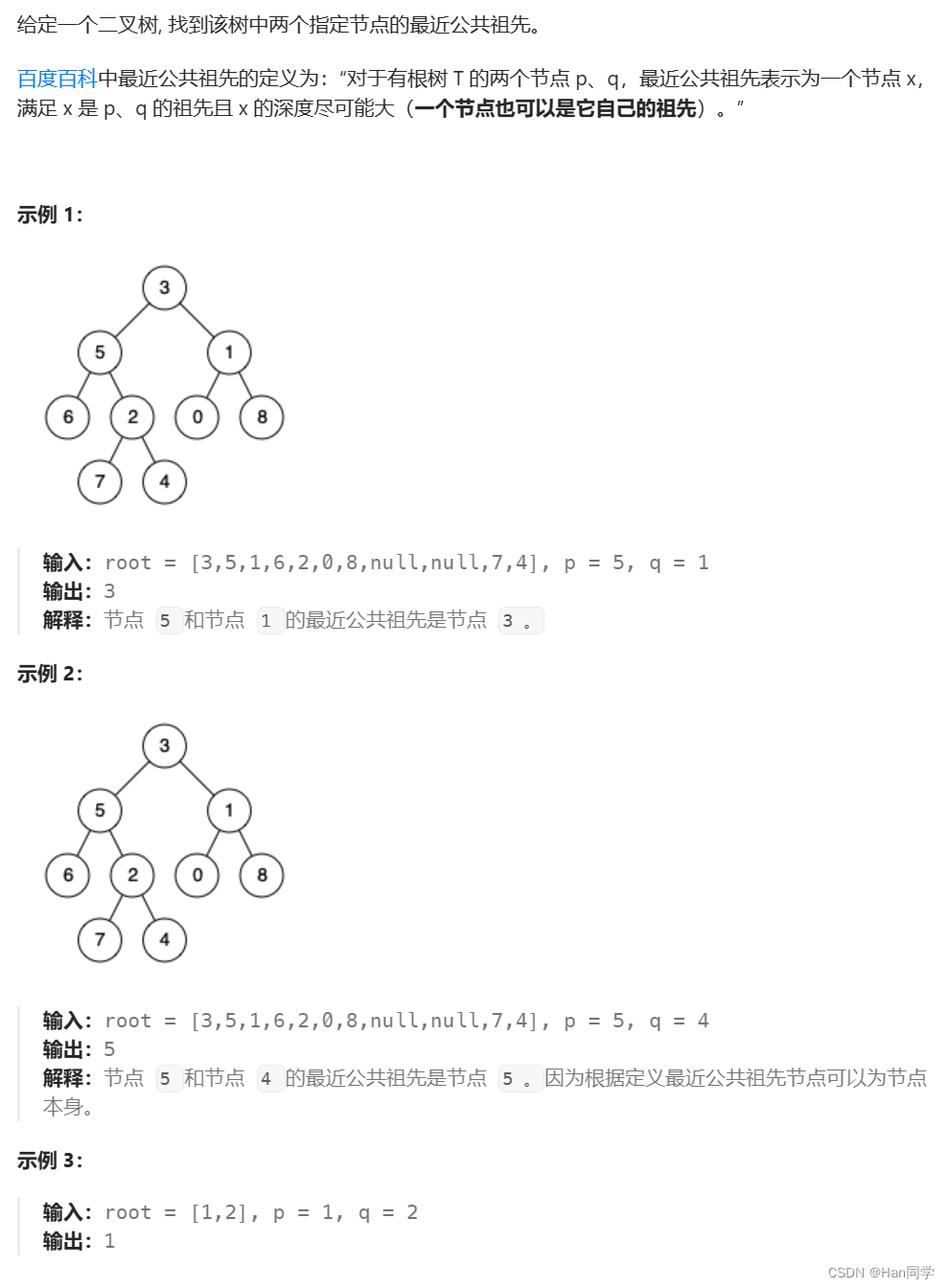
第一种思路：

  • 如果一个在节点的左树一个在节点的右树，那这个节点就是公共祖先。
  • 如果二者都在根节点的同一颗子树（左子树或右子树），转换为子问题，到对应子树找公共祖先。
class Solution {
public:
    bool InsInTree(TreeNode* root, TreeNode* x) {
        if (root == nullptr)
            return false;

        return root == x || InsInTree(root->left, x) ||
               InsInTree(root->right, x);
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root == nullptr)
            return nullptr;

        if (p == root || q == root)
            return root;

        bool pInleft = InsInTree(root->left, p);
        bool pInRight = !pInleft;

        bool qInleft = InsInTree(root->left, q);
        bool qInRight = !qInleft;

        if ((pInLeft && qInRight) || (qInLeft && pInRight))
            return root;
        else if (pInLeft && qInLeft)
            return lowestCommonAncestor(root->left, p, q);
        else
            return lowestCommonAncestor(root->right, p, q);
    }
};
  1. 如果根节点是空的，那么返回空。
  2. 如果根节点就是我们要找的其中一个节点，那么返回根节点。
  3. 然后，我们检查两个节点是否在根节点的左子树或右子树中。这是通过调用IsInTree函数实现的，这个函数会递归地在子树中查找目标节点。
  4. 如果两个节点分别在根节点的左子树和右子树中，那么根节点就是他们的最低公共祖先。
  5. 如果两个节点都在左子树中，那么我们在左子树中递归地查找他们的最低公共祖先。
  6. 如果两个节点都在右子树中，那么我们在右子树中递归地查找他们的最低公共祖先。

这个算法的时间复杂度是O(N^2)，其中N是二叉树的节点数。这是因为对于每个节点，我们都可能需要在其子树中查找目标节点，这需要O(N)的时间。而我们可能需要对每个节点都做这样的操作，所以总的时间复杂度是O(N^2)。

空间复杂度是O(N)，这是因为在最坏的情况下，我们可能需要递归地访问所有的节点，这会在调用栈上产生O(N)的空间。

这个算法的时间复杂度可以进一步优化，时间复杂度可以降低到O(N)。

第二种思路：计算二者路径进行比较。时间复杂度：O(N)。

通过获取两个节点的路径，然后比较路径上的节点，找到最低公共祖先节点。它使用了栈来存储路径，通过递归遍历二叉树来获取路径。最后，通过比较栈中的节点，找到最低公共祖先节点并返回。

class Solution {
public:
    bool GetPath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path) {
        if (root == nullptr)
            return false;
        path.push(root);
        if (root == x)
            return true;
        if (GetPath(root->left, x, path))
            return true;
        if (GetPath(root->right, x, path))
            return true;
        path.pop();
        return false;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        stack<TreeNode*> pPath, qPath;
        GetPath(root, p, pPath);
        GetPath(root, q, qPath);
        while (qPath.size() != pPath.size()) {
            if (pPath.size() > qPath.size())
                pPath.pop();
            else
                qPath.pop();
        }
        while (pPath.top() != qPath.top()) {
            pPath.pop();
            qPath.pop();
        }
        return qPath.top();
    }
};

  1. GetPath 函数用于获取从根节点到目标节点的路径，并将路径上的节点存储在一个栈中。它采用递归的方式进行遍历。

  2. lowestCommonAncestor 函数是主要的解决方案函数。它首先创建两个栈 pPath 和 qPath，分别用于存储节点 p 和节点 q 的路径。

  3. 调用 GetPath 函数两次，分别获取节点 p 和节点 q 的路径，并将路径存储在对应的栈中。

  4. 接下来，使用一个循环来比较两个路径的长度，直到它们的长度相等为止。如果 pPath 的长度大于 qPath 的长度，则从 pPath 栈中弹出顶部节点；否则，从 qPath 栈中弹出顶部节点。这样，两个栈的长度将相等。

  5. 最后，使用另一个循环来比较 pPath 和 qPath 栈顶的节点，直到找到最低公共祖先节点为止。每次比较时，都从两个栈中同时弹出顶部节点。

  6. 返回 qPath 栈顶的节点作为最低公共祖先节点。

5、JZ36 二叉搜索树与双向链表

class Solution {
  public:
    void InOrder(TreeNode* cur, TreeNode*& prev) {
        if (cur == nullptr)
            return;
        InOrder(cur->left, prev);
        cur->left = prev;
        if (prev)
            prev->right = cur;
        prev = cur;
        InOrder(cur->right, prev);
    }
    TreeNode* Convert(TreeNode* pRootOfTree) {
        TreeNode* prev = nullptr;
        InOrder(pRootOfTree, prev);
        TreeNode* head = pRootOfTree;
        while (head && head->left) {
            head = head->left;
        }
        return head;
    }
};
  • 首先，我们定义了一个TreeNode结构体，它包含一个整数值val，以及左右子节点的指针left和right。这个结构体用于表示二叉树的节点。
  • 接下来是Solution类，其中包含了两个函数：InOrder和Convert。
  • InOrder函数是一个递归函数，用于进行中序遍历并完成转换。它接受两个参数：当前节点cur和前一个节点prev的引用。
    • 在函数内部，首先进行递归调用InOrder函数来处理当前节点的左子树。然后，将当前节点的左指针指向prev，将prev的右指针指向当前节点（如果prev不为空）。最后，更新prev为当前节点。接着，继续递归调用InOrdert函数来处理当前节点的右子树。
  • 在Convert函数内部，首先定义一个指针prev，并初始化为nullptr。然后调用InOrder函数来完成中序遍历和转换。最后，通过循环找到双向链表的头节点，即最左侧的节点，将其赋值给head，并返回head。

6、105. 从前序与中序遍历序列构造二叉树

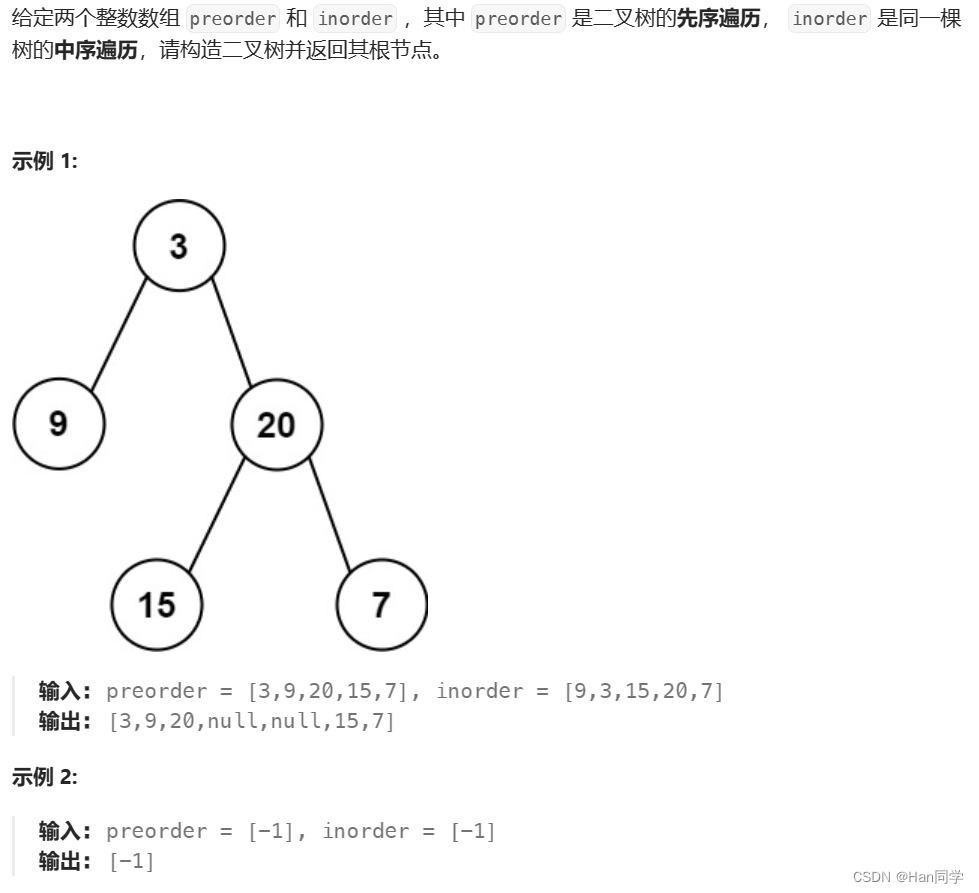
思路： 根据前序遍历结果创建根节点，然后根据中序遍历结果确定左子树和右子树的范围，再递归构建左子树和右子树，最后返回构建好的二叉树根节点。

class Solution {
public:
    TreeNode* _buildTree(vector<int>& preorder, vector<int>& inorder, int& prei,
                         int inbegin, int inend) {
        if (inbegin > inend)
            return nullptr;
        TreeNode* root = new TreeNode(preorder[prei]);
        int rooti = inbegin;
        while (rooti <= inend) {
            if (inorder[rooti] == preorder[prei])
                break;
            else
                rooti++;
        }
        ++prei;
        root->left = _buildTree(preorder, inorder, prei, inbegin, rooti - 1);
        root->right = _buildTree(preorder, inorder, prei, rooti + 1, inend);
        return root;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int i = 0;
        return _buildTree(preorder, inorder, i, 0, inorder.size() - 1);
    }
};

  1. _buildTree 函数是一个递归函数，用于构建二叉树。它接受前序遍历结果 preorder、中序遍历结果 inorder、前序遍历索引 prei、中序遍历起始索引 inbegin 和中序遍历结束索引 inend 作为参数。

  2. 首先，检查中序遍历的起始索引 inbegin 是否大于结束索引 inend，如果是，则返回空指针，表示当前子树为空。

  3. 创建一个新的节点 root，节点的值为前序遍历索引 prei 对应的值。

  4. 初始化一个变量 rooti，用于记录当前节点在中序遍历结果中的索引。从 inbegin 开始遍历中序遍历结果，直到找到与当前节点值相等的节点为止。

  5. 增加前序遍历索引 prei 的值，以便下一次递归调用时可以获取下一个节点的值。

  6. 递归调用 _buildTree 函数构建当前节点的左子树，传入前序遍历结果 preorder、中序遍历结果 inorder、前序遍历索引 prei、中序遍历起始索引 inbegin 和 rooti - 1。

  7. 递归调用 _buildTree 函数构建当前节点的右子树，传入前序遍历结果 preorder、中序遍历结果 inorder、前序遍历索引 prei、rooti + 1 和中序遍历结束索引 inend。

  8. 返回当前节点 root。

  9. buildTree 函数是主要的解决方案函数。它初始化一个变量 i 为 0，并调用 _buildTree 函数来构建整个二叉树，传入前序遍历结果 preorder、中序遍历结果 inorder、前序遍历索引 i、中序遍历起始索引 0 和中序遍历结束索引 inorder.size() - 1。

  10. 返回构建好的二叉树的根节点。

 

7、106. 从中序与后序遍历序列构造二叉树

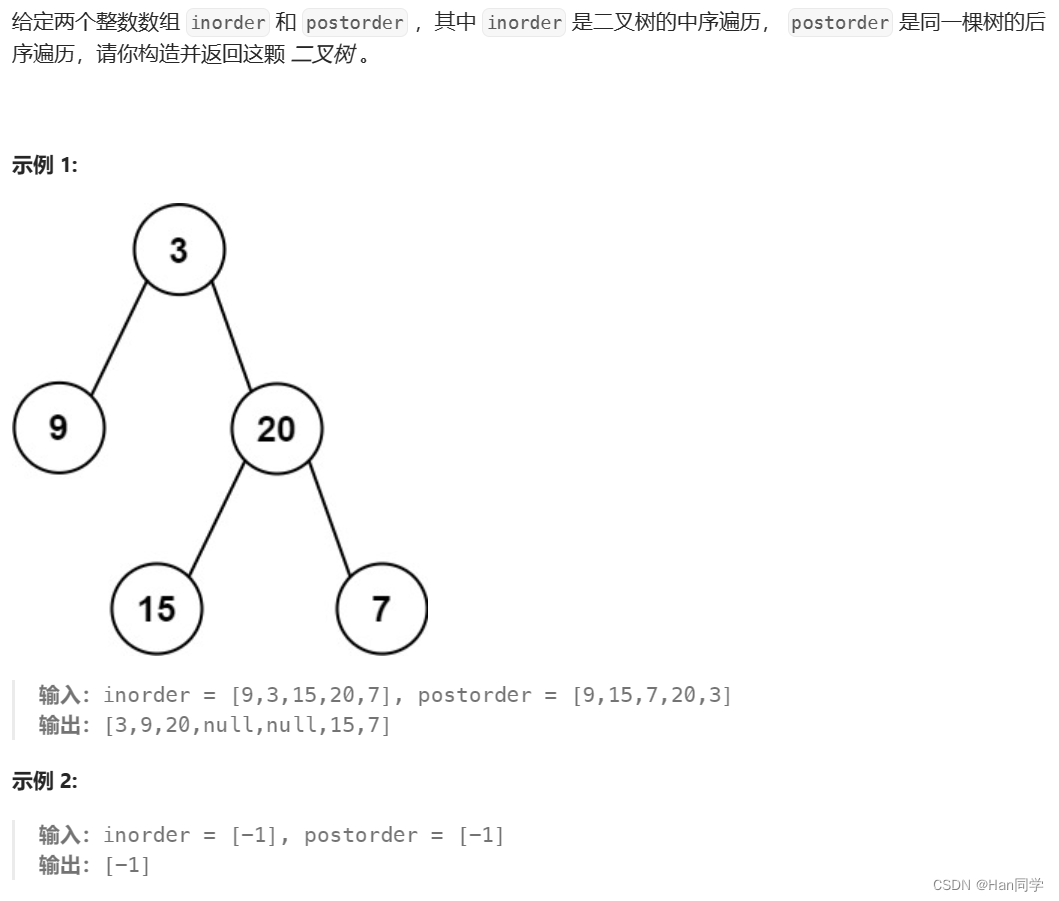
思路：根据后续遍历结果创建根节点，然后根据中序遍历结果确定左子树和右子树的范围，再递归构建左子树和右子树，最后返回构建好的二叉树根节点。 

class Solution {
public:
    TreeNode* _buildTree(vector<int>& postorder, vector<int>& inorder,
                         int& posi, int inbegin, int inend) {
        if (inbegin > inend)
            return nullptr;
        TreeNode* root = new TreeNode(postorder[posi]);
        int rooti = inbegin;
        while (rooti <= inend) {
            if (inorder[rooti] == postorder[posi])
                break;
            else
                rooti++;
        }
        --posi;
        root->right = _buildTree(postorder, inorder, posi, rooti + 1, inend);
        root->left = _buildTree(postorder, inorder, posi, inbegin, rooti - 1);
        return root;
    }
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int i = postorder.size() - 1;
        return _buildTree(postorder, inorder, i, 0, inorder.size() - 1);
    }
};

  1. _buildTree 函数是一个递归函数，用于构建二叉树。它接受后序遍历结果 postorder、中序遍历结果 inorder、后序遍历索引 posi、中序遍历起始索引 inbegin 和中序遍历结束索引 inend 作为参数。

  2. 首先，检查中序遍历的起始索引 inbegin 是否大于结束索引 inend，如果是，则返回空指针，表示当前子树为空。

  3. 创建一个新的节点 root，节点的值为后序遍历索引 posi 对应的值。

  4. 初始化一个变量 rooti，用于记录当前节点在中序遍历结果中的索引。从 inbegin 开始遍历中序遍历结果，直到找到与当前节点值相等的节点为止。

  5. 减小后序遍历索引 posi 的值，以便下一次递归调用时可以获取下一个节点的值。

  6. 递归调用 _buildTree 函数构建当前节点的右子树，传入后序遍历结果 postorder、中序遍历结果 inorder、后序遍历索引 posi、rooti + 1 和中序遍历结束索引 inend。

  7. 递归调用 _buildTree 函数构建当前节点的左子树，传入后序遍历结果 postorder、中序遍历结果 inorder、后序遍历索引 posi、中序遍历起始索引 inbegin 和 rooti - 1。

  8. 返回当前节点 root。

  9. buildTree 函数是主要的解决方案函数。它初始化一个变量 i 为后序遍历结果的最后一个索引，并调用 _buildTree 函数来构建整个二叉树，传入后序遍历结果 postorder、中序遍历结果 inorder、后序遍历索引 i、中序遍历起始索引 0 和中序遍历结束索引 inorder.size() - 1。

  10. 返回构建好的二叉树的根节点

8、144. 二叉树的前序遍历

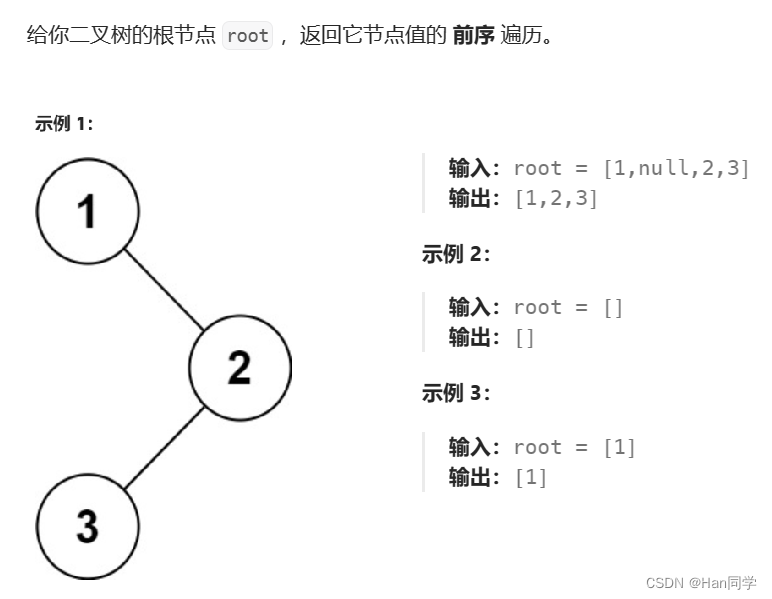
非递归： 

思路：

  • 首先，我们创建一个栈 st 来存储节点。我们将根节点 root 赋值给当前节点 cur。
  • 然后，我们使用一个循环来遍历树，条件是当前节点不为空或者栈不为空。在循环中，我们首先进入一个内部循环，将当前节点及其值加入栈 st 和结果向量 v 中，并将当前节点更新为其左子节点，直到当前节点的左子树为空。
  • 当内部循环结束后，我们取出栈顶的节点 top，将其右子节点赋值给当前节点 cur。这样，我们就完成了对当前节点的左子树的遍历。
  • 整个过程会一直持续到当前节点为空且栈为空，即遍历完整个二叉树。
  • 最后，我们返回结果向量 v，其中存储了前序遍历的结果。 
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        vector<int> v;
        while (cur || !st.empty()) {
            while (cur) {
                v.push_back(cur->val);
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            st.pop();
            cur = top->right;
        }
        return v;
    }
};

​

递归：

class Solution {
public:
    void preorder(TreeNode* root, vector<int>& ret) {
        if (root == nullptr) {
            return;
        }
        ret.push_back(root->val);
        preorder(root->left, ret);
        preorder(root->right, ret);
    }

    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ret;
        preorder(root, ret);
        return ret;
    }
};

9、94. 二叉树的中序遍历

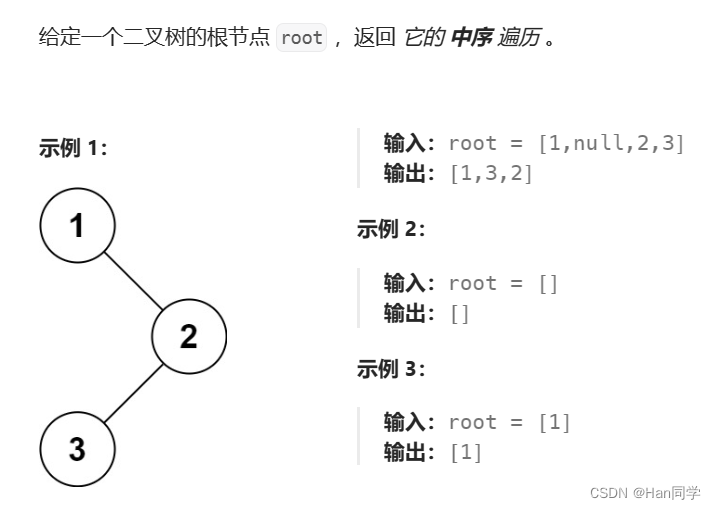
非递归： 

思路：继承非递归的前序遍历思路，存入数组的时机需要更改。 

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        vector<int> v;
        while (cur || !st.empty()) {
            while (cur) {
                st.push(cur);
                cur = cur->left;
            }
            TreeNode* top = st.top();
            st.pop();
            v.push_back(top->val);
            cur = top->right;
        }
        return v;
    }
};

​

递归： 

class Solution {
public:
    void inorder(TreeNode* root, vector<int>& ret) {
        if (root == nullptr)
            return;
        inorder(root->left, ret);
        ret.push_back(root->val);
        inorder(root->right, ret);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        inorder(root, ret);
        return ret;
    }
};

10、145. 二叉树的后序遍历

非递归：  

 思路：通过栈来模拟递归的过程。先遍历左子树，然后遍历右子树，最后访问根节点。通过维护一个 prev 指针来判断右子树是否已经被访问过，从而确定是否可以访问当前的根节点。

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        vector<int> v;
        TreeNode* prev = nullptr;
        while (cur || !st.empty()) {
            while (cur) {
                st.push(cur);
                cur = cur->left;
            }
            
            TreeNode* top = st.top();

            //右为空，或者 右子树已经访问过了(上一个访问的节点是右子树的根)，可以访问根节点
            if (top->right == nullptr || top->right == prev) {
                v.push_back(top->val);
                st.pop();
                prev = top;
            } else {
                cur = top->right;
            }
        }
        return v;
    }
};

递归： 

class Solution {
public:
    void postorder(TreeNode *root, vector<int> &ret) {
        if (root == nullptr) {
            return;
        }
        postorder(root->left, ret);
        postorder(root->right, ret);
        ret.push_back(root->val);
    }

    vector<int> postorderTraversal(TreeNode *root) {
        vector<int> ret;
        postorder(root, ret);
        return ret;
    }
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1396432.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

pdf怎么查看？6个不能错过的软件！

pdf怎么查看？6个不能错过的软件！

PDF&#xff0c;作为一种常用的文件格式&#xff0c;已经成为了我们工作、学习中的必备工具。然而&#xff0c;对于许多新手来说&#xff0c;如何查看和编辑PDF文件却是一个不小的挑战。今天&#xff0c;我们就来为大家详细介绍一下如何查看和编辑PDF文件&#xff0c;以及一些必…
阅读更多...
从法律的角度看待项目前期可行性研究的必要性

从法律的角度看待项目前期可行性研究的必要性

前言 在司法实践中&#xff0c;很多纠纷展现出来的问题是项目提供方没有按照合同约定履行发生违约的情况&#xff0c;例如逾期交付、项目不符合约定标准等等&#xff0c;但是这些情况发生的原因是各不相同的&#xff0c;其中有一类纠纷的发生却是从一开始就埋下了风险的种子&a…
阅读更多...
2.0-学成在线内容管理

2.0-学成在线内容管理

内容管理模块 1.需求 1.1 业务流程 内容管理的业务由教学机构人员和平台的运营人员共同完成。 教学机构人员的业务流程如下&#xff1a; 1、登录教学机构。 2、维护课程信息&#xff0c;添加一门课程需要编辑课程的基本信息、上传课程图片、课程营销信息、课程计划、上传课程…
阅读更多...
深入详解使用 RabbitMQ 过程中涉及到的多个细节问题（面试可用）

深入详解使用 RabbitMQ 过程中涉及到的多个细节问题（面试可用）

目录 1、基础类问题 2、cluster 相关问题 3、综合性问题 4、参考资料 C软件异常排查从入门到精通系列教程&#xff08;专栏文章列表&#xff0c;欢迎订阅&#xff0c;持续更新...&#xff09;https://blog.csdn.net/chenlycly/article/details/125529931C/C基础与进阶&…
阅读更多...
OB OCP工具

OB OCP工具

文章目录 OCP产品架构OCP核心功能集群管理-集群拓扑图告警管理 OCP OCP&#xff08;OceanBase Cloud Platform&#xff09;是企业级数据库管理平台OceanBase 云平台&#xff08;OceanBase Cloud Platform&#xff0c;OCP&#xff09;是以 OceanBase 为核心的企业级数据库管理平…
阅读更多...
外汇天眼：加拿大监管机构提出了关于持有加密资产的公共投资基金的规定

外汇天眼：加拿大监管机构提出了关于持有加密资产的公共投资基金的规定

加拿大证券管理局&#xff08;CSA&#xff09;是由加拿大各省金融市场监管机构组成的国家机构。他们已发布了一组旨在征求意见的拟议监管要求&#xff0c;适用于寻求投资加密资产的公共投资基金。 Stan Magidson&#xff0c;CSA主席兼艾伯塔证券委员会主席兼首席执行官表示&…
阅读更多...
无货源跨境电商到底应该怎么做，新手必看

无货源跨境电商到底应该怎么做，新手必看

如今&#xff0c;跨境电商无疑已经成为了一个热门的创业领域&#xff0c;但对于一些新手来说&#xff0c;面临的一个主要挑战是如何处理产品的货源问题。下面我就和大家分享一下无货源跨境电商的基本概念以及一些新手可以采取的策略和步骤&#xff0c;帮助大家在这个领域取得成…
阅读更多...
UE4 添加按键输入事件 并在蓝图中使用按键输入节点

UE4 添加按键输入事件 并在蓝图中使用按键输入节点

绑定按键 选择Edit/ProjectSettings/Engine/Input 在bindings中可以选择添加ActionMappings或则AxisMappings ActionMappings:按键事件&#xff0c;有按下和抬起两个事件&#xff0c;需要分别用两个键触发AxisMappings:输入事件&#xff0c;返回值为float&#xff0c;对于键盘…
阅读更多...
突破划片机技术瓶颈，博捷芯BJX3352助力晶圆切割行业升级

突破划片机技术瓶颈，博捷芯BJX3352助力晶圆切割行业升级

随着半导体行业的快速发展&#xff0c;晶圆切割作为半导体制造过程中的重要环节&#xff0c;对于切割设备的性能和精度要求越来越高。为了满足市场需求&#xff0c;提高生产效率&#xff0c;国产划片机企业博捷芯推出了新一代划片机BJX3352&#xff0c;成功突破了技术瓶颈&…
阅读更多...
(设置非自定义Bean)学习Spring的第六天

(设置非自定义Bean)学习Spring的第六天

一 . 获取Bean的方法详解 , 如下图 : 二 . Spring配置非自定义bean----DruidDatasource 我们举个例子 : 配置Druid数据源交由Spring管理 首先导入在pom文件Druid坐标 然后考虑 : 被配置的Bean的实例化方式是什么 : 无参构造 被配置的Bena是否要注入必要属性 : 四个基本信息…
阅读更多...
msvcp140_atomic_wait.dll文件缺失的解决方法指南，如何快速修复

msvcp140_atomic_wait.dll文件缺失的解决方法指南，如何快速修复

在处理计算机软件时&#xff0c;我们经常遭遇一些阻碍程序运行的错误&#xff0c;尤其是那些与动态链接库(DLL)文件相关的。msvcp140_atomic_wait.dll是一个常见的DLL文件&#xff0c;它在Windows操作系统中扮演了重要角色。本文将讨论msvcp140_atomic_wait.dll文件的作用&…
阅读更多...
小程序导出excel

小程序导出excel

先上个图&#xff0c;这个是在电脑上测试导出来的表 大致远离就是用的原生td&#xff0c;tr去导出的&#xff0c; 代码 <template><view><button click"tableToExcel">导出一个表来看</button></view> </template><script&g…
阅读更多...
《Python数据分析技术栈》第01章 02 Jupyter入门（Getting started with Jupyter notebooks）

《Python数据分析技术栈》第01章 02 Jupyter入门（Getting started with Jupyter notebooks）

02 Jupyter入门&#xff08;Getting started with Jupyter notebooks&#xff09; 《Python数据分析技术栈》第01章 02 Jupyter入门&#xff08;Getting started with Jupyter notebooks&#xff09; Before we discuss the essentials of Jupyter notebooks, let us discuss…
阅读更多...
C语言编译和链接

C语言编译和链接

翻译环境和运行环境 在ANSI C的任何一种实现中&#xff0c;存在两个不同的环境 .第一种是翻译环境&#xff0c;在这个环境中源代码被转换为可执行的机器指令 .第二种是执行环境&#xff0c;它用于实际执行代码 翻译环境 翻译环境是由编译和链接两个大过程组成&#xff0c;而…
阅读更多...
公域＋私域，打造流量池最好的方式

公域＋私域，打造流量池最好的方式

阅读更多...
仿真机器人-深度学习CV和激光雷达感知(项目2)day03【机器人简介与ROS基础】

仿真机器人-深度学习CV和激光雷达感知(项目2)day03【机器人简介与ROS基础】

文章目录 前言机器人简介机器人应用与前景机器人形态机器人的构成 ROS基础ROS的作用和特点ROS的运行机制ROS常用命令 前言 &#x1f4ab;你好&#xff0c;我是辰chen&#xff0c;本文旨在准备考研复试或就业 &#x1f4ab;本文内容是我为复试准备的第二个项目 &#x1f4ab;欢迎…
阅读更多...
RT-Thread 瑞萨 智能家居网络开发：RA6M3 HMI Board 以太网+GUI技术实践

RT-Thread 瑞萨 智能家居网络开发：RA6M3 HMI Board 以太网+GUI技术实践

不用放大了&#xff0c; 我在包里找到张不小的…… 以太网HMI线下培训-环境准备 名字虽然叫技术培训&#xff1a; 其实是由两部分组成&#xff1a;板子网关 先介绍周六的培训是啥&#xff0c;然后再介绍一下要准备的一些东西 R A 6 M 3 H M I − B o a r d \textcolor{#41…
阅读更多...
AD导出BOM表 导出PDF

AD导出BOM表 导出PDF

1.Simple BOM: 这种模式下&#xff0c;最好在pcb界面&#xff0c;这样的导出的文件名字是工程名字&#xff0c;要是在原理图界面导出&#xff0c;会以原理图的名字命名表格。 直接在菜单栏 报告->Simple BOM 即可导出物料清单&#xff0c;默认导出 comment pattern qu…
阅读更多...
LaTeX-OCR安装教程

LaTeX-OCR安装教程

一. 通用安装步骤 1.前置应用 安装LaTeX-OCR首先需要安装Python。在系统自带的应用商店Microsoft Store搜索Python&#xff0c;点击最新版本Python 3.12下载即可。 2.运行powershell Win11按底部状态栏windows徽标在搜索框内搜索 powershell 或者按快捷键 “win 键 R” &am…
阅读更多...
GO基础进阶篇 (十四)、Http编程

GO基础进阶篇 (十四)、Http编程

Web基础概念 web应用程序 web程序可以提供浏览器访问的程序。Web应用程序通常采用客户端-服务器模型。客户端是用户使用的Web浏览器或其他Web客户端&#xff0c;而服务器是存储和处理数据的远程计算机。 我们能访问到的任何一个页面或资源&#xff0c;都存在于世界的某一个角落…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023