2018年认证杯SPSSPRO杯数学建模
基于轮廓提取与图像配准的零件定位问题研究
C题 机械零件加工过程中的位置识别
原题再现:
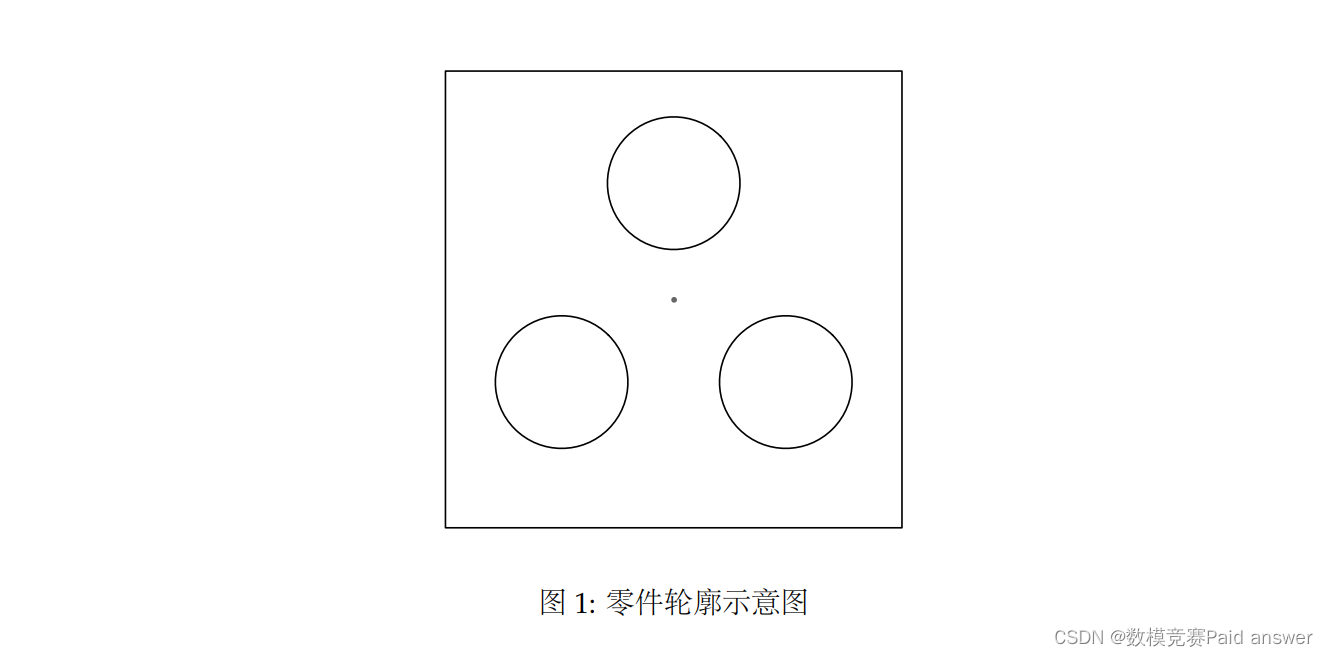
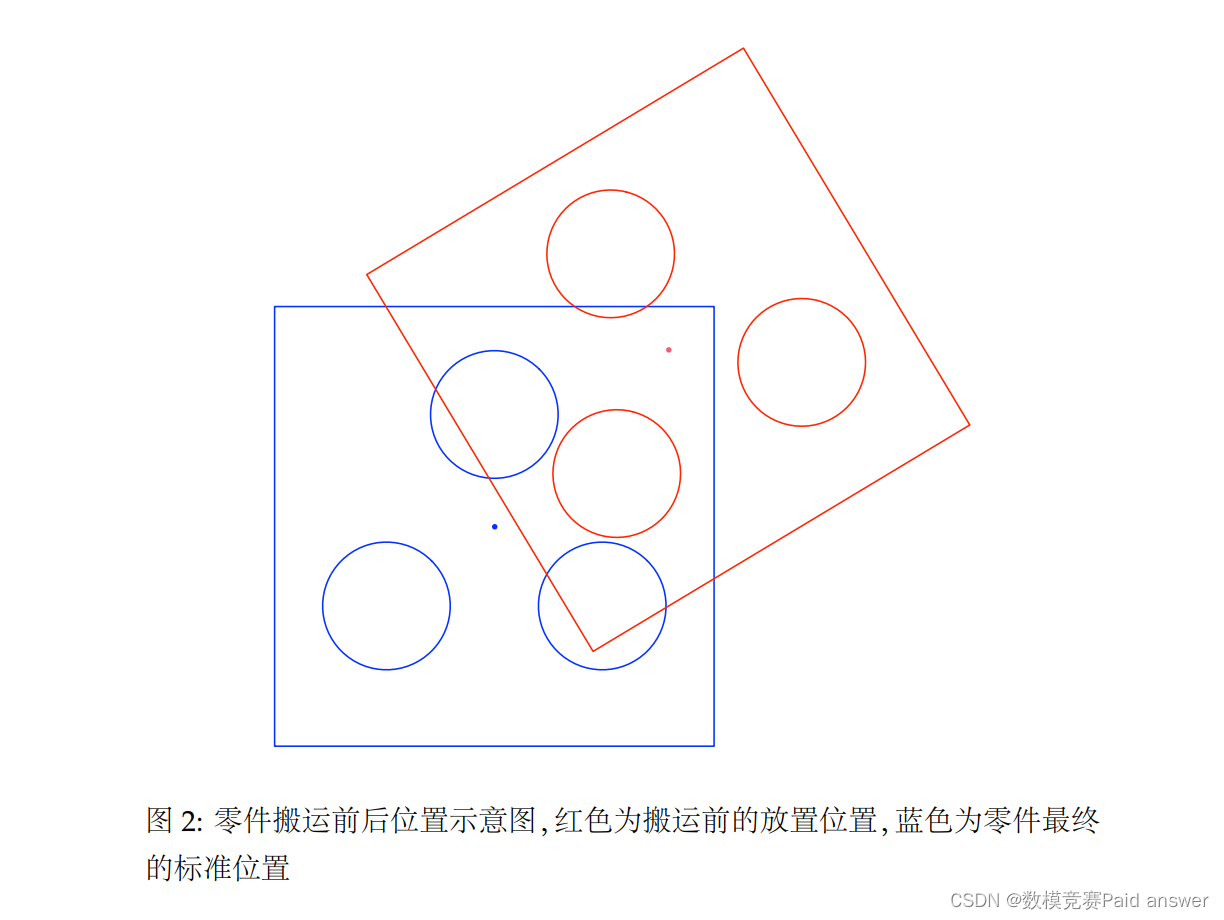
在工业制造自动生产线中,在装夹、包装等工序中需要根据图像处理利用计算机自动智能识别零件位置,并由机械手将零件自动搬运到特定位置。某零件轮廓如图 1 所示,图2 表示零件搬运前后的位置示意图。
第二阶段问题:
3. 题目给出了未经轮廓提取的原始零件图像数据 (附件 DATA3),请采用或自主设计合适的轮廓提取算法,验证前两问中建立的优化模型是否同样适用。
4. 问题 1 至问题 3 讨论的是零件放置于平面的情况。假设零件放置在不平整的表面上,请建立有效的数学模型,识别不同零件的位置 (开放性问题,自主设计)。
整体求解过程概述(摘要)
在本文中,我们主要对工业生产中零件的轮廓提取和当零件放置于不平整的表面上时的定位问题进行了研究。
本文的主要创新点:首先我们研究了提取零件轮廓的算法,提出了通过 Canny 和watershed 算法相结合的适用范围较广并且效果相对较好的轮廓提取算法,在三维情况下,我们通过将基准图片与实际的图片进行配准,并通过基准坐标获取实际坐标的方式,在兼顾效率的同时实现了三维空间较好的定位算法。以下是我们主要完成的工作:
对于轮廓提取问题,需要考虑零件的内部轮廓是否对结果有影响,如果没有影响,使用 watershed 算法对零件的外部轮廓进行提取;当存在影响时,则采取改进的 Canny算法同时对内部和外部轮廓进行提取;两种方法各有利弊,watershed 提取的轮廓信息不全,适用领域有限,而 Canny 算法提取的零件边缘往往有较多的噪声,我们将二者相结合从而实现适用范围更广,效果更好的算法。当轮廓提取完成后,通过寻找关键点的方式可以计算出零件的坐标,以题目中给出的四个齿轮中最大的一个为例,由于其本身存在的对称性,我们提取其几何中心,内部的长方形与其外轮廓一侧的两个交点作为其坐标,当移动该齿轮时,只需要将这三个点的位置放到目标位置上即可完成操作,最终得到的结果为(342, 159), (350, 126), (496.5, 232.0)。
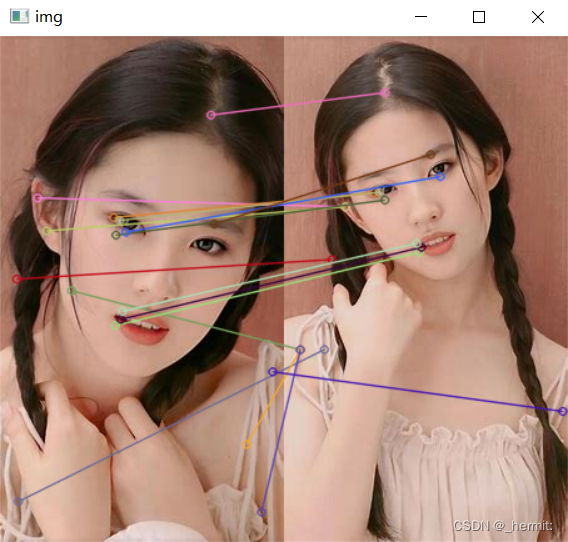
当零件放置于不平整的表面时,仅通过一张图片很难得到想要的信息,所以要解决这个问题,需要至少两张图片,通过 SURF 算法对这两张图片进行图像配准,并且计算出两张图片中零件的变换矩阵,假设对于机械臂所到达的每一个位置,我们有其基准的位置坐标,通过这些基准坐标,加上通过变换所得到的基准图像中的关键点的坐标最终得到目标零件的坐标信息。我们的结果具有较好的泛化能力,不仅能处理不考虑高度的二维坐标,对于三维坐标也同样适用。
在对模型进行介绍和求解之后,我们对其进行了评价,分析了其优缺点,并对潜在的应用场景进行了探讨。
问题分析:
本阶段的题目主要分为两个大问题以及四个子问题,首先是在假设平面平整的前提下,为所的零件俯视图像中零件的识别与轮廓的提取算法的设计,这其中需要预先对图像进行预处理以保证轮廓算法的高效与精准;其次是考虑更为复杂的情况,即平明不平整的前提下,建立数学模型识别不同零件的位置,在识别位置之前首先要考虑三维空间转二维空间物体发生的形变并对这种形变进行转换与处理。
问题三的具体分析
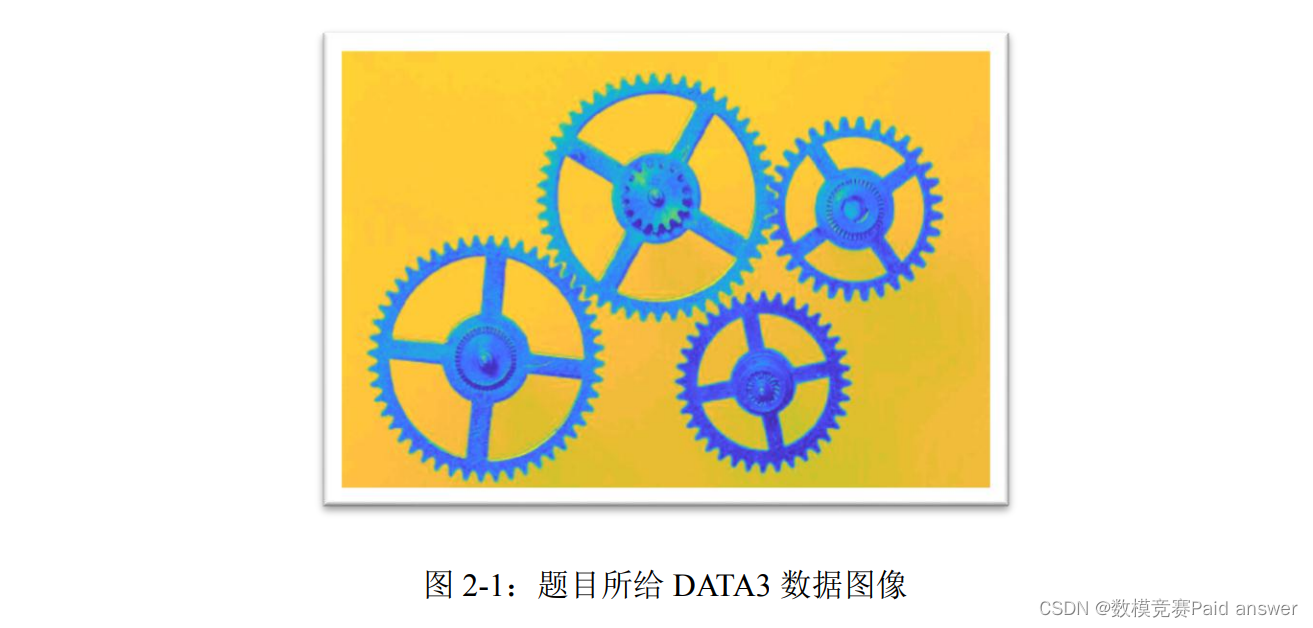
问题三给出了一个未经轮廓提取的原始零件图像数据,经过图像查看为四个齿轮的图像。与第一阶段的问题一和二中的正方形与三个异构圆孔明显不同,虽然齿轮整体是一个对称的零件,但是由于其边缘呈现锯齿形状,在零件抓取与定位的过程中对齿轮的边缘细节的提取要求较高。
首先,需要对图像进行预处理,将彩色的图像数据降低维度,进而对图像进行灰度及二值换处理。并且需要对图像进行滤波、去噪等预处理,以便后期高效的处理。
其次,可根据分水岭算法及形态学等对预处理过的图像进行齿轮外轮廓的提取,因仅提取齿轮的外轮廓,则可进行多种处理。其中需注意,因左、上、右三个齿轮咬合较为紧密,在数据分割时难免会造成咬合部分轮廓的缺失,若发生此类情况,需根据齿轮的特性进行整个齿轮外径轮廓的补全。
最后,因仅根据外形轮廓无法支持对定位的要求,还需要得到内径及孔洞的轮廓数据信息,可根据 Canny 算法对整体的所有齿轮的所有孔洞及内外径进行整体的轮廓提取,并且将整体轮廓与上一步的加强外径轮廓进行融合,将得到非常明显且精准的平面内多零件的整体清晰轮廓图像数据。
问题四的具体分析
问题四的情况则更为复杂,因前三个问题均发生在平整平面内,即仅 x 与 y的坐标发生位移,即仅在二维坐标内发生位移。但如整体的情况为非平整平面,则零件会在 z 轴也发生位移,即零件会在三维空间内发生位移及旋转。虽然零件在三维空间内发生了旋转,但从摄像机的俯视角度,仅能看到二维形状发生的形变,这将为计算位移与旋转角度带来极大的困难。

因此,将采用对空间及尺寸变换不敏感的算法,如 surf 算法对基准图像与现有零件放置图像进行图像配准,通过两个图像特征值的配准的过程求得三维空间内的转换矩阵,由矩阵数据可求得两个零件在三维空间内的相对位移。最终零件当前的位置可由基准位置的坐标及相对位移求得。
模型假设:
假设 1:附件提供的零件位置数据在可靠条件下获得,光照稳定、无明显抖动,摄像机摄像效果良好;
假设 2:零件的结构标准,即在单一齿轮中锯齿结构相同;
假设 3:多个零件在平台上的摆放并没有重叠;
假设 4:针对问题三情况,物体摆放平整,且图像数据均为俯视图。
假设 5:针对问题四情况,物体虽然放置在不平整的平面,会发声一定的倾斜,但非进行视角转换,并未进行轴旋转类空间形变。并且有基准位置的图片库。
论文缩略图:



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
clear all;
clear
clc;
%读进图像
[filename, pathname] = uigetfile({'*.jpg'; '*.bmp'; '*.gif'}, '选择图片');
%没有图像
if filename == 0
return;
end
imgsrc = imread([pathname, filename]);
[y, x, dim] = size(imgsrc);
%转换为灰度图
if dim>1
imgsrc = rgb2gray(imgsrc);
end
for i = 1:10
imgsrc = medfilt2(imgsrc);
end
sigma = 1;
gausFilter = fspecial('gaussian', [3,3], sigma);
img= imfilter(imgsrc, gausFilter, 'replicate');
zz = double(img);
%----------------------------------------------------------
%自己的边缘检测函数?
[m theta sector canny1 canny2 bin] = canny1step(img, 22);
[msrc thetasrc sectorsrc c1src c2src binsrc] = canny1step(imgsrc, 22);
%Matlab 自带的边缘检测?
ed = edge(img, 'canny', 0.5);
[xx, yy] = meshgrid(1:x, 1:y);
m = uint8(m);
figure(1)
imshow(m)
imwrite(m, '无二值化.jpg')
m = imbinarize(m);
for i = 1:2
m = medfilt2(m);
end
figure(2)
imshow(m);
imwrite(m, '二值化.jpg')
save image.mat
function [ m, theta, sector, canny1, canny2, bin] = canny1step( src,
lowTh)
%canny 函数第一步,求去 x,y 方向的偏导,模板如下:
% Gx
% 1 -1
% 1 -1
% Gy
% -1 -1
% 1 1
%------------------------------------
% 输入:
% src:图像,如果不是灰度图转成灰度图
% lowTh:低阈值
% 输出:
% m: 两个偏导的平方差,反映了边缘的强度
% theta:反映了边缘的方向
% sector:将方向分为 3 个区域,具体如下
% 2 1 0
% 3 X 3
% 0 1 2
% canny1:非极大值
% canny2:双阈值抑制
% bin : 二值化
%---------------------------------------
[Ay Ax dim ] = size(src);
%转换为灰度图
if dim>1
src = rgb2gray(src);
end
src = double(src);
m = zeros(Ay, Ax);
theta = zeros(Ay, Ax);
sector = zeros(Ay, Ax);
canny1 = zeros(Ay, Ax);%非极大值抑制
canny2 = zeros(Ay, Ax);%双阈值检测和连接
bin = zeros(Ay, Ax);
for y = 1:(Ay-1)
for x = 1:(Ax-1)
gx = src(y, x) + src(y+1, x) - src(y, x+1) - src(y+1, x+1);
gy = -src(y, x) + src(y+1, x) - src(y, x+1) + src(y+1, x+1);
m(y,x) = (gx^2+gy^2)^0.5 ;
%--------------------------------
theta(y,x) = atand(gx/gy) ;
tem = theta(y,x);
%--------------------------------
if (tem<67.5)&&(tem>22.5)
sector(y,x) = 0;
elseif (tem<22.5)&&(tem>-22.5)
sector(y,x) = 3;
elseif (tem<-22.5)&&(tem>-67.5)
sector(y,x) = 2;
else
sector(y,x) = 1;
end
%--------------------------------
end
end
%-------------------------
%非极大值抑制
%------> x
% 2 1 0
% 3 X 3
%y 0 1 2
for y = 2:(Ay-1)
for x = 2:(Ax-1)
if 0 == sector(y,x) %右上 - 左下
if ( m(y,x)>m(y-1,x+1) )&&( m(y,x)>m(y+1,x-1) )
canny1(y,x) = m(y,x);
else
canny1(y,x) = 0;
end
elseif 1 == sector(y,x) %竖直方向
if ( m(y,x)>m(y-1,x) )&&( m(y,x)>m(y+1,x) )
canny1(y,x) = m(y,x);
else
canny1(y,x) = 0;
end
elseif 2 == sector(y,x) %左上 - 右下
if ( m(y,x)>m(y-1,x-1) )&&( m(y,x)>m(y+1,x+1) )
canny1(y,x) = m(y,x);
else
canny1(y,x) = 0;
end
elseif 3 == sector(y,x) %横方向
if ( m(y,x)>m(y,x+1) )&&( m(y,x)>m(y,x-1) )
canny1(y,x) = m(y,x);
else
canny1(y,x) = 0;
end
end
end%end for x
end%end for y
%---------------------------------
%双阈值检测
ratio = 2;
for y = 2:(Ay-1)
for x = 2:(Ax-1)
if canny1(y,x)<lowTh %低阈值处理
canny2(y,x) = 0;
bin(y,x) = 0;
continue;
elseif canny1(y,x)>ratio*lowTh %高阈值处理
canny2(y,x) = canny1(y,x);
bin(y,x) = 1;
continue;
else %介于之间的看其 8 领域有没有高于高阈值的,有则可以
为边缘
tem =[canny1(y-1,x-1), canny1(y-1,x), canny1(y-1,x+1);
canny1(y,x-1), canny1(y,x),
canny1(y,x+1);
canny1(y+1,x-1), canny1(y+1,x),
canny1(y+1,x+1)];
temMax = max(tem);
if temMax(1) > ratio*lowTh
canny2(y,x) = temMax(1);
bin(y,x) = 1;
continue;
else
canny2(y,x) = 0;
bin(y,x) = 0;
continue;
end
end
end%end for x
end%end for y
end%end of function