主要记录个人思考过程，不同方案实现思路的演变

题目

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

思路一

当时大脑出现的第一想法就是先找找规律

• f(1) = 1
• f(2) = 2
• f(3) = 3
• f(4) = 5
• f(5) = 8
  发现除了1 和2 剩下的规律就是前面两个相加 于是有了这样的公式
  f(n) = f(n-1) + f(n-2)
  代码实现如下：

class Solution {
    public int climbStairs(int n) {
            if(n==1){
                return 1;
            }
            if(n== 2){
                return 2;
            }
            return climbStairs(n-1) + climbStairs(n-2);
    }
}

在LeetCode 提交

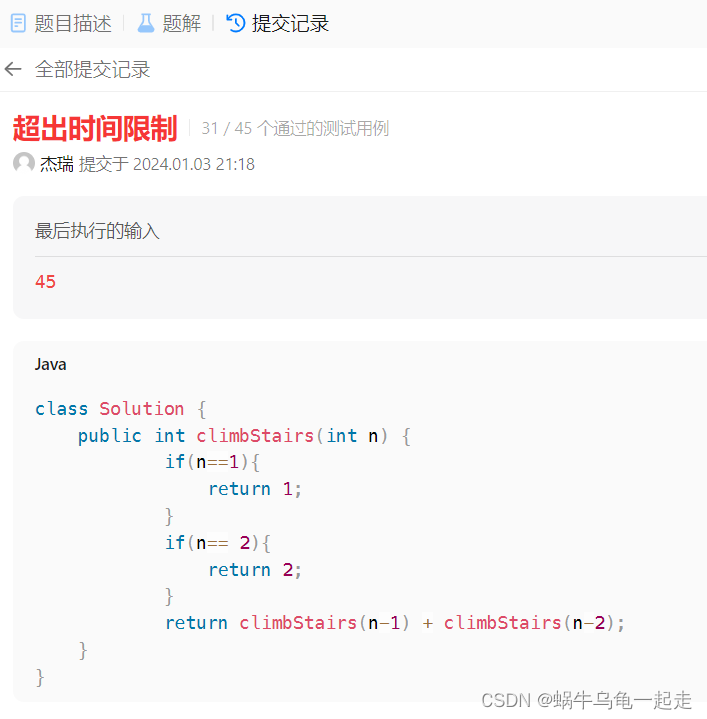
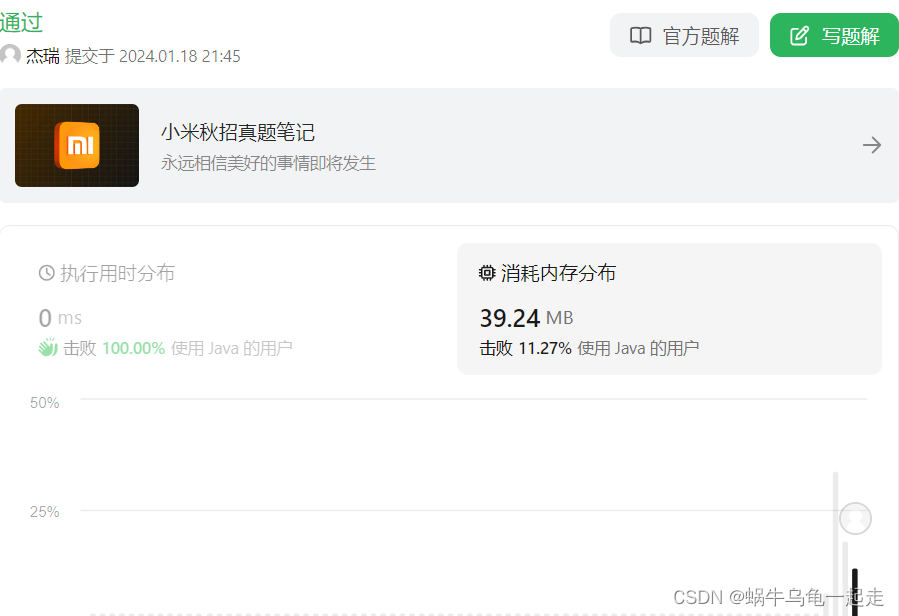
可以看到超時了，看来代码么问题但是性能存在问题，问题根源就在于每次都是重新计算。如何不重新计算就是使用空间换区时间思路，把每次记录存储下来，不需要重新计算。

思路二

代码实现

public int climbStairs(int n) {
        int[] s = new int[n];
        return getValue(0,n,s);
    }

    private int getValue(int i, int n, int[] s) {
        if (i > n) {
            return 0;
        }
        if (n == i) {
            return 1;
        }
        if (s[i] > 0) {
            return s[i];
        }
        s[i] = getValue(i + 1,n,s) + getValue(i + 2,n,s);
        return s[i];
    }

提交后如图，显示通过

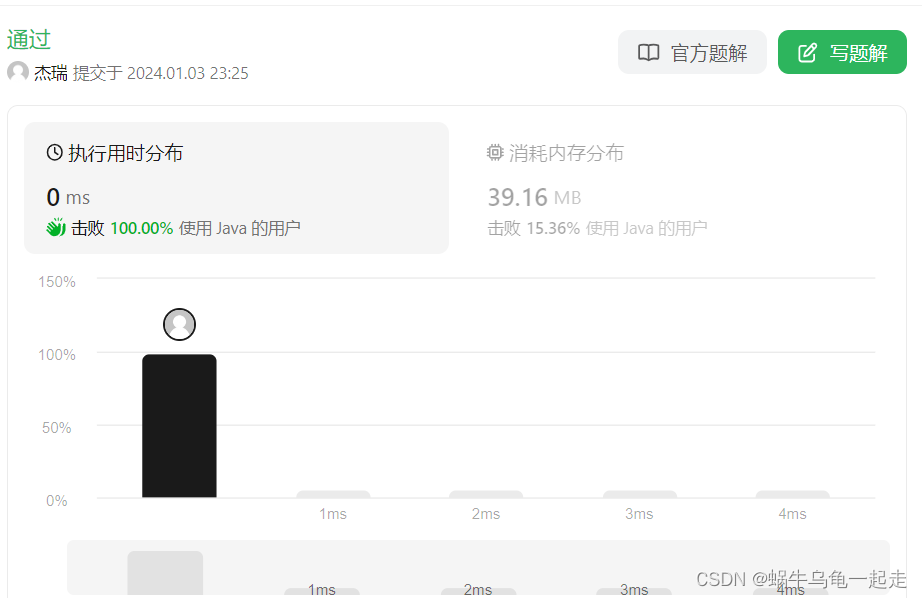
后来又觉得不够优雅 代码质量差，还是用到递归了，在想想是否可以 不使用递归呢？同时又可以使用空间换去时间，不用重复计算。使用循环赋值实现即可

思路三

代码如下

 public int climbStairs(int n) {
        if(n == 1){
            return 1;
        }
        int[] s = new int[n+1];
        s[1] = 1;
        s[2] = 2;
        for(int i =3;i <= n; i++){
            s[i] = s[i-1] + s[i-2];
        }
        return s[n];
    }

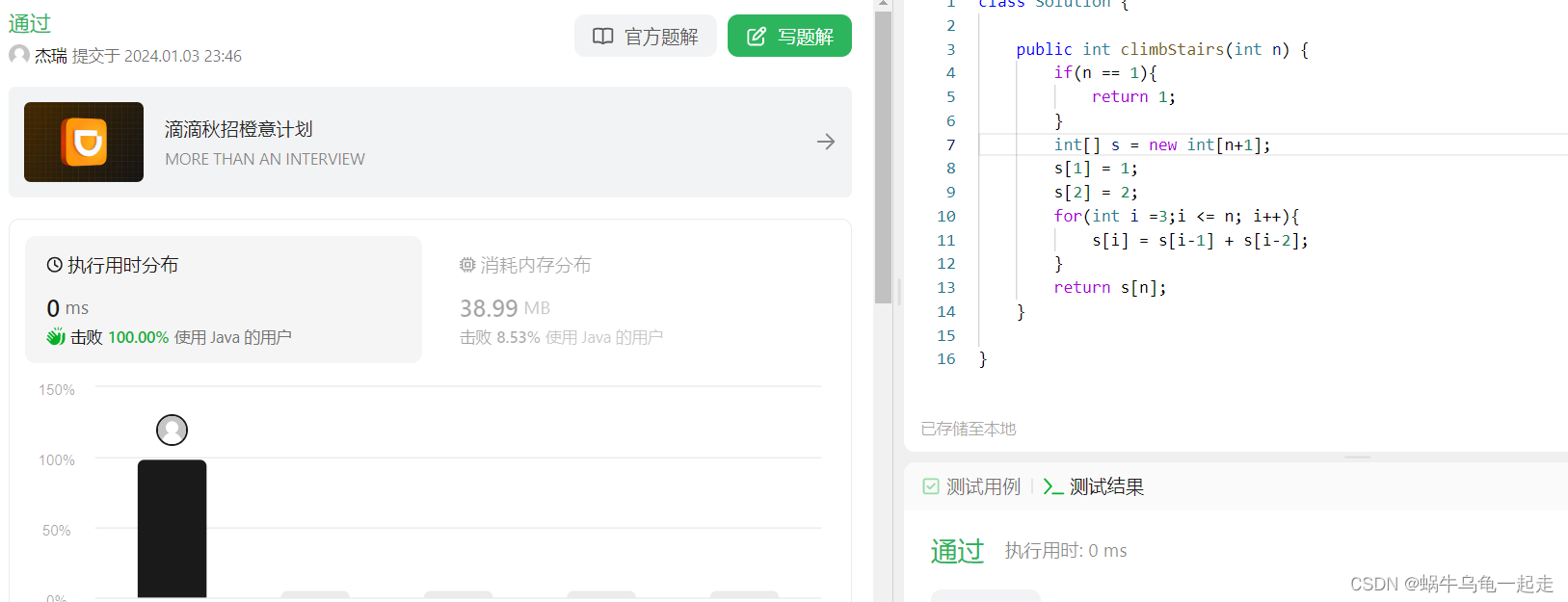
可以看到使用的内存相比第二思路有较少了。

思路四

网上参考网友思路看到另一种解法，使用局部变量存储值 实现如下

 public int climbStairs(int n) {
        if (n == 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }

        int a = 1;
        int b = 2;
        int sum = 0;
        for (int i = 3; i <= n; i++) {
            sum =  a;
            a = b;
            sum = sum + a;
            b = sum;
        }
        return sum;
    }