Git将某个文件合并到指定分支
news2026/2/12 9:42:06
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1393704.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
线上党建展厅有哪些功能,如何搭建一个成功的线上党建展厅
引言:
随着互联网的飞速发展,线上党建展厅成为党建宣传的新平工具,它提供了一个方便的党建学习、交流和展示的空间。那么线上党建展厅有哪些功能,如何搭建一个成功的线上党建展厅呢? 一、线上党建展厅有哪些功能
1.组…
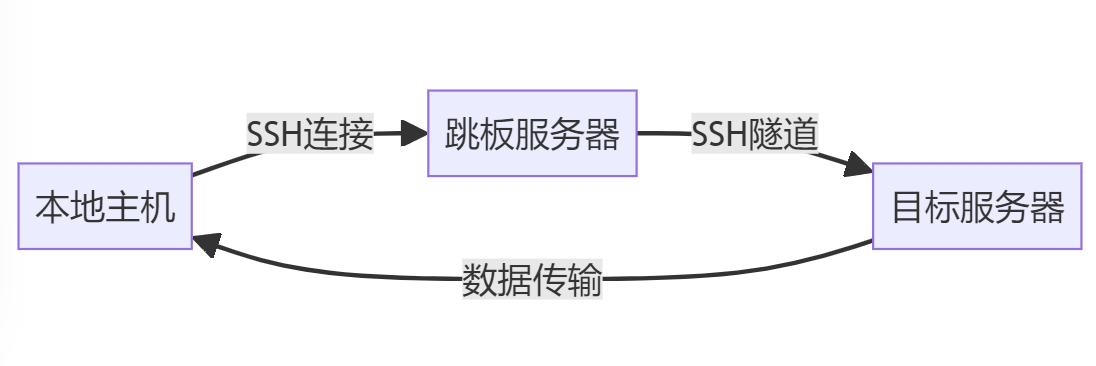
SSH 隧道是什么,有什么用
本地主机(A):需要访问目标服务器的主机。 跳板服务器(B):位于本地主机和目标服务器之间的第三方服务器。跳板服务器上已经配置好SSH服务,并允许SSH隧道传输。 目标服务器(Cÿ…
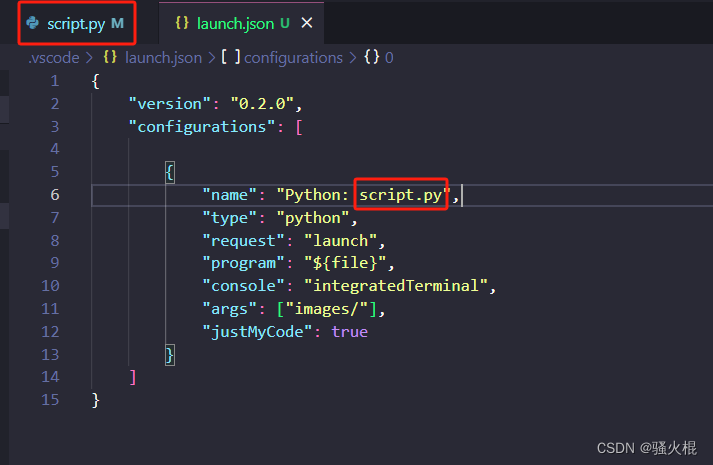
vscode调试debug,launch.json文件‘args’无法发传递给脚本
问题:调试时,脚本执行,发现在launch.json文件中明明定义了“args”参数,却没有传递给执行命令。
解决:
launch.json中的"name"参数不要随便起,要与执行的文件名一致! 参考链接&…
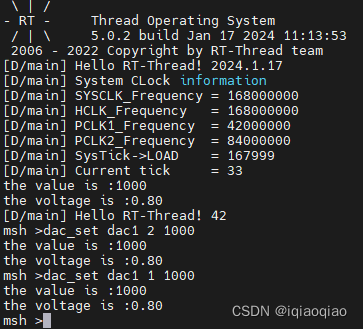
RT-Thread Studio学习(十三)DAC
RT-Thread Studio学习(十三)DAC 一、简介二、新建RT-Thread项目并使用外部时钟三、启用DAC四、测试五、总结 一、简介
本文将基于STM32F407VET芯片介绍如何在RT-Thread Studio开发环境下使用DAC设备。硬件及开发环境如下:
OS WIN10STM32F40…
聆听人生故事:欧美用户与“爱可声”助听器的相伴时刻
在日常生活中,听力下降是一种常见的问题,尤其在年长者中更为普遍。随着人口老龄化的加剧,助听器市场也在不断扩大。据世界卫生组织发布的《世界听力报告》显示,目前全球五分之一的人听力受损,听力损失影响全球超过15亿…
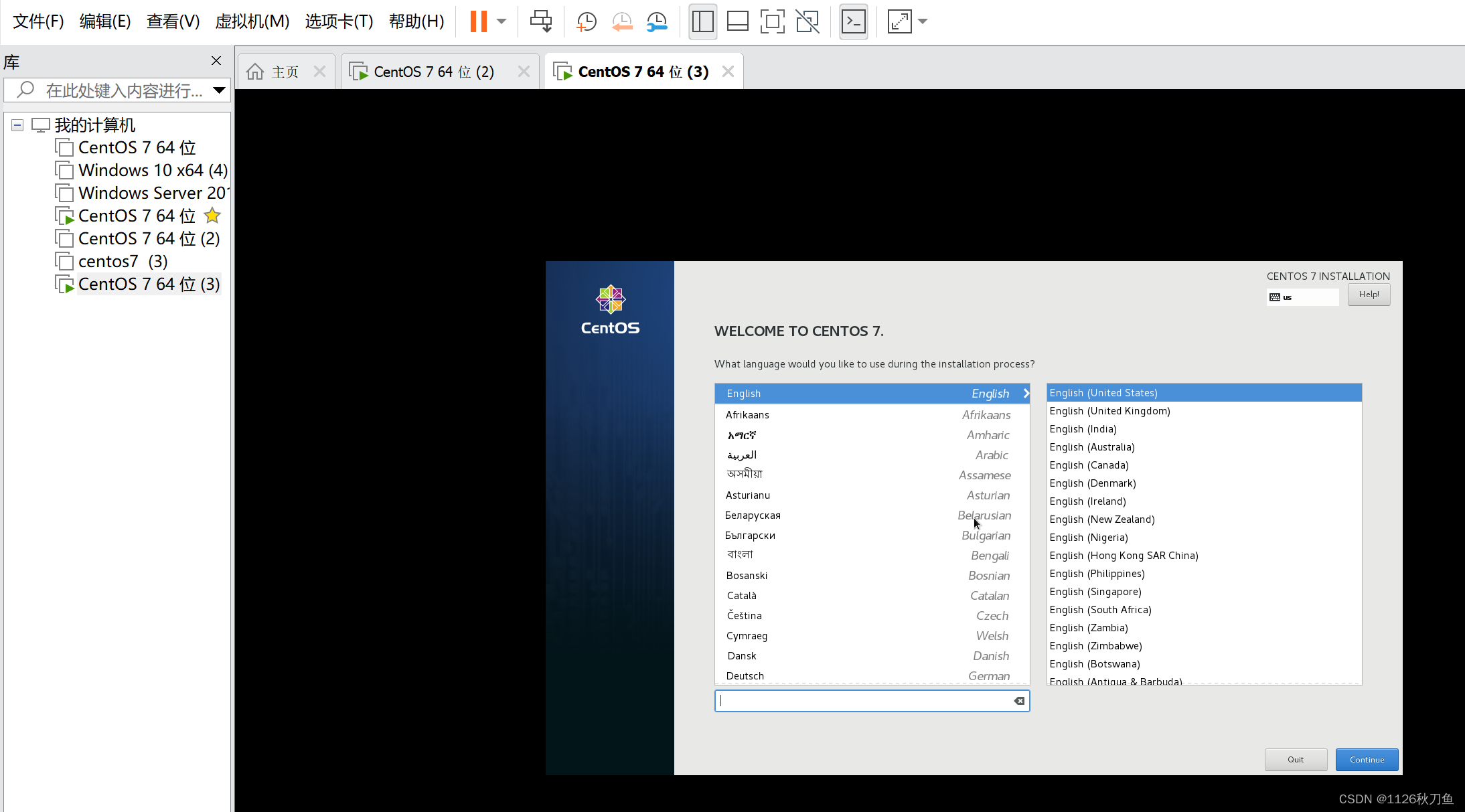
pxe高效批量网络装机 以及安装教程
系统装机的三种引导模式
1.pe
2光驱
3.网卡 打开本机桌面 可以看见背景图片 查看配置文件内容 文件时引导选项的功能 pxe原理:
先根据dhcp找到IP地址、和引导程序的地址,还提供客户机tftp地址,因为tftp是小文件,容量小&#…
龙芯3A6000_统信UOS上使用UDOM工具箱
原文链接:龙芯3A6000|统信UOS上使用UDOM工具箱 大家好!今天,我非常兴奋地和大家分享一篇关于在龙芯3A6000搭载统信UOS系统上使用UDOM工具箱的实用指南。这不仅是一次技术探索,也是一次提升运维效率的旅程。 首先,让我们…
【NPL】自然语言处理(Natural Language Processing,NLP)的发展简述
大家好,我是全栈小5,欢迎阅读文章! 此篇是【话题达人】序列文章,这一次的话题是《自然语言处理的发展》 文章将以博主的角度进行讲述,理解和水平有限,不足之处,望指正。 目录 背景发展线路研发关…
Jira 宣布Data Center版涨价5%-15%,6年内第8次提价
近日,Atlassian官方面向合作伙伴发布2024年涨价通知:
自2024年2月15日起,旗下核心产品Jira Software、Confluence、Jira Service Management的DC版本(Data Center版本)价格提高5%-15%(涨幅与坐席数阶梯相关…
关于C#中的async/await的理解
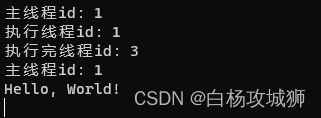
1. 使用async标记的方法被认为是一个异步方法,如果不使用await关键字,调用跟普通方法没有区别 static async Task Main(string[] args){Console.WriteLine("主线程id:" Thread.CurrentThread.ManagedThreadId);TestAwait();Consol…
数字身份所有权:Web3时代用户数据的掌控权
随着Web3时代的来临,数字身份的概念正焕发出崭新的光芒。在这个数字化的时代,用户的个人数据变得愈加珍贵,而Web3则为用户带来了数字身份所有权的概念,重新定义了用户与个人数据之间的关系。本文将深入探讨Web3时代用户数据的掌控…
1127: 矩阵乘积
题目描述
计算两个矩阵A和B的乘积。
输入
第一行三个正整数m、p和n,0<m,n,p<10,表示矩阵A是m行p列,矩阵B是p行n列;
接下来的m行是矩阵A的内容,每行p个整数,用空格隔开;
最后的p行是矩…
C++大学教程(第九版)5.15修改GradeBook
目录
题目
代码
运行命令(在控制台输入)
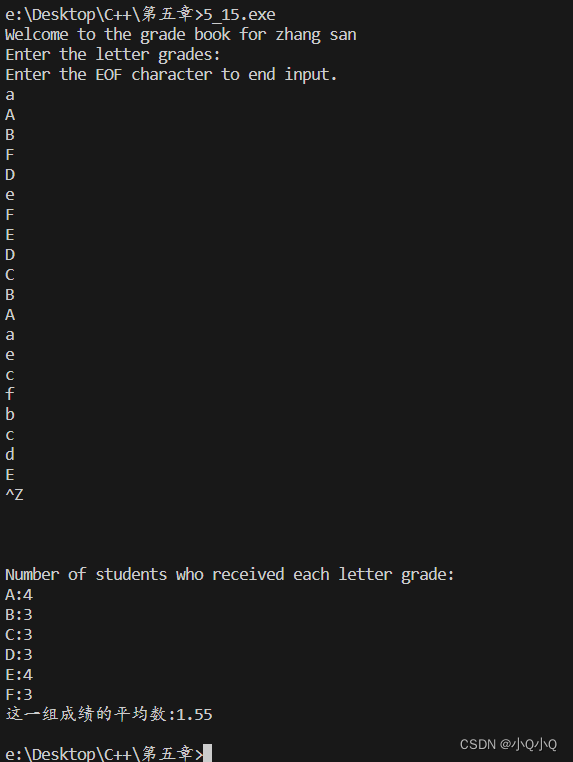
运行截图 题目
(修改GradeBook)修改图5.9~图5.11所示的 GradeBook 程序,使它计算一组成绩的平均成绩。 成绩A为4分,成绩B为3分,依次类推。 A:4 B:3…
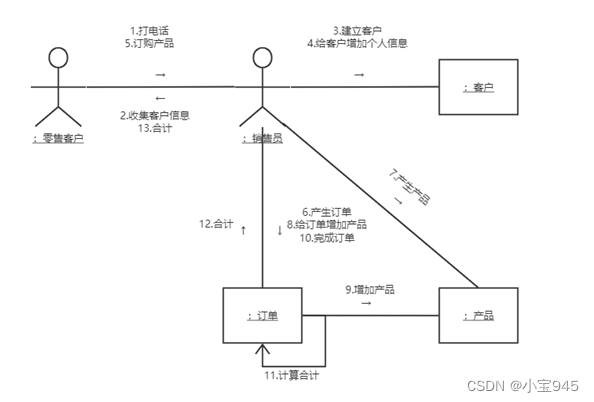
UML-通信图和交互概览图(通信图和顺序图的区别与联系)
UML-通信图和交互概览图(通信图和顺序图的区别与联系) 一、通信图简介1.消息2.链接 二、通信图和[顺序图](https://blog.csdn.net/weixin_65032328/article/details/135587782)的联系与区别三、交互概览图四、顺序图转化为通信图练习 一、通信图简介
通…
Docker部署Flask项目
Docker部署Flask项目 一、准备项目代码二、编写Dockerfile三、服务器部署 一、准备项目代码
这里写了一个简单的Flask的demo,源代码如下:
from flask import Flaskapp Flask(__name__)app.route("/")
def index():return "<h1 styl…
软件测试面试200问(含答案)
🍅 视频学习:文末有免费的配套视频可观看 🍅 关注公众号【互联网杂货铺】,回复 1 ,免费获取软件测试全套资料,资料在手,涨薪更快 1、B/S架构和C/S架构区别
B/S 只需要有操作系统和浏览器就行&a…
线程、线程创建、多线程、线程同步
程序:为完成特定任务,使用计算机语言编写的一系列指令集合,即静态代码。
进程:正在执行的程序,操作系统分配资源的最小单位。
线程:进程内部最小执行单位。(具体要做的一件事情)
…
CAN FD数据脱机记录仪的在汽车应用上的优势
CAN FD数据脱机记录仪的优势
大容量存储:CAN FD数据脱机记录仪通常具备大容量的存储空间,可以记录长时间的CAN数据。这使得它非常适合于需要长时间记录CAN数据的场景,例如车辆测试、故障诊断等。
离线处理:CAN FD数据脱机记录仪…
python数字图像处理基础(七)——直方图均衡化、傅里叶变换
目录 直方图均衡化均衡化原理均衡化效果标准直方图均衡化自适应直方图均衡化 傅里叶变换原理低通滤波高通滤波 直方图均衡化
均衡化原理
图像均衡化是一种基本的图像处理技术,通过更新图像直方图的像素强度分布来调整图像的全局对比度。这样做可以使低对比度的区域…